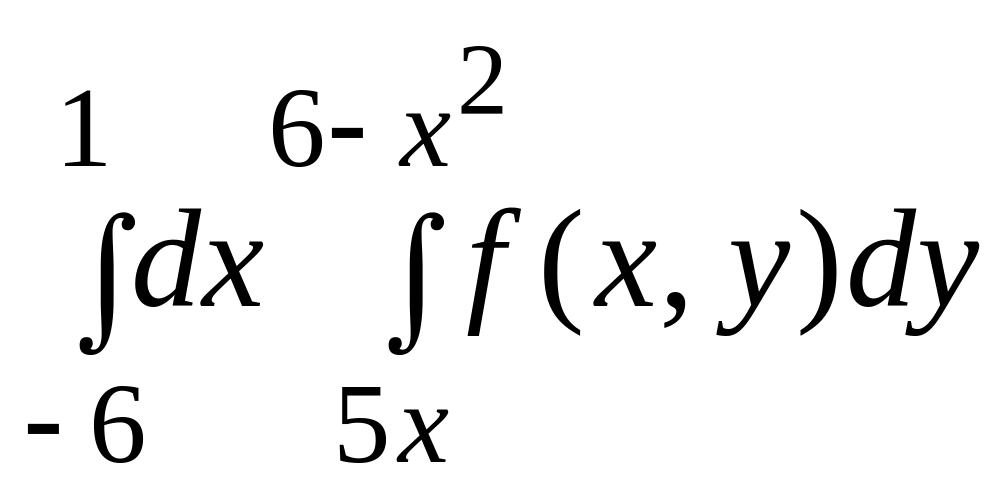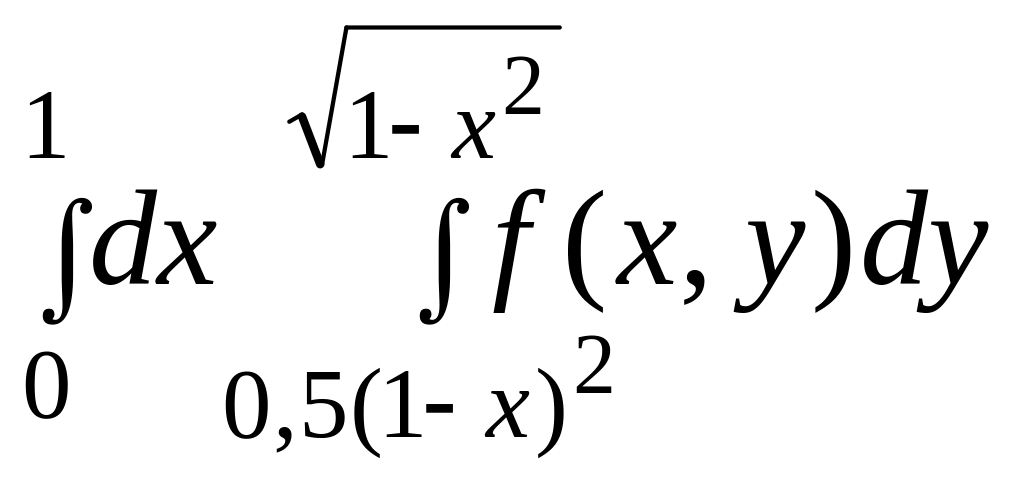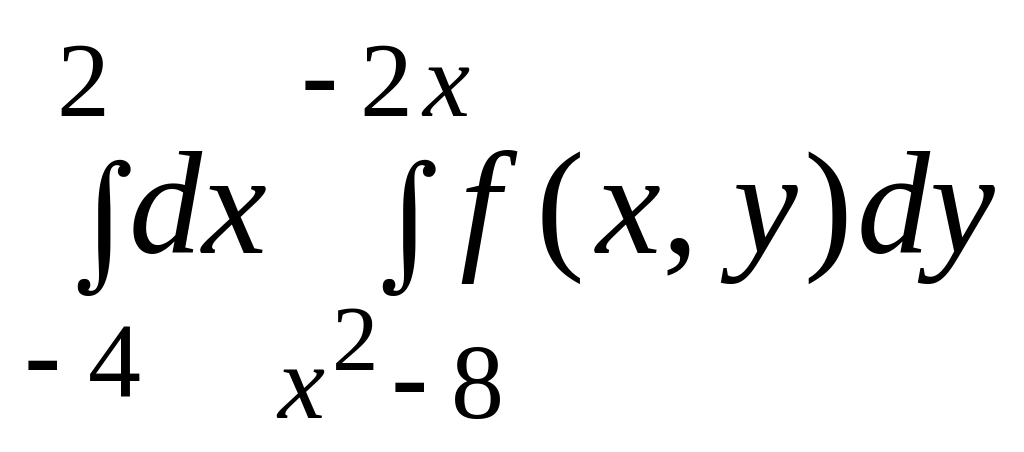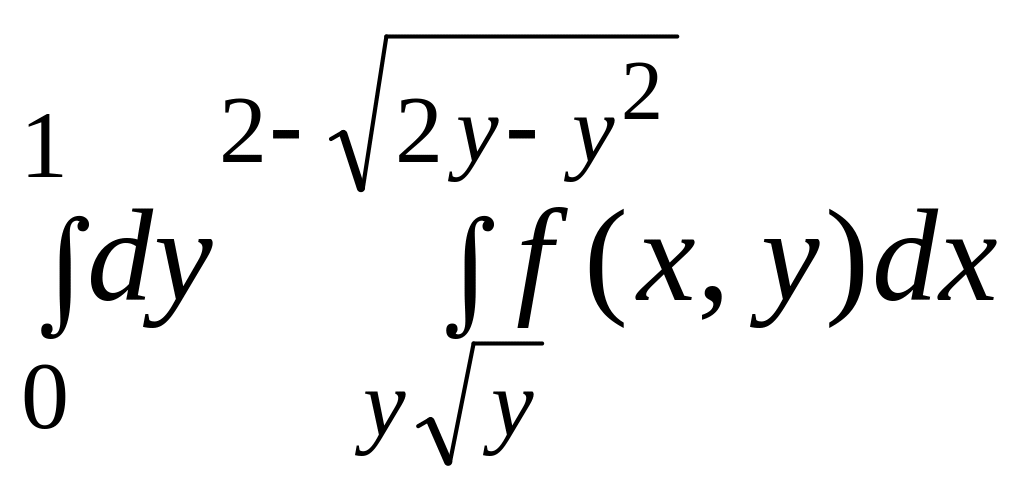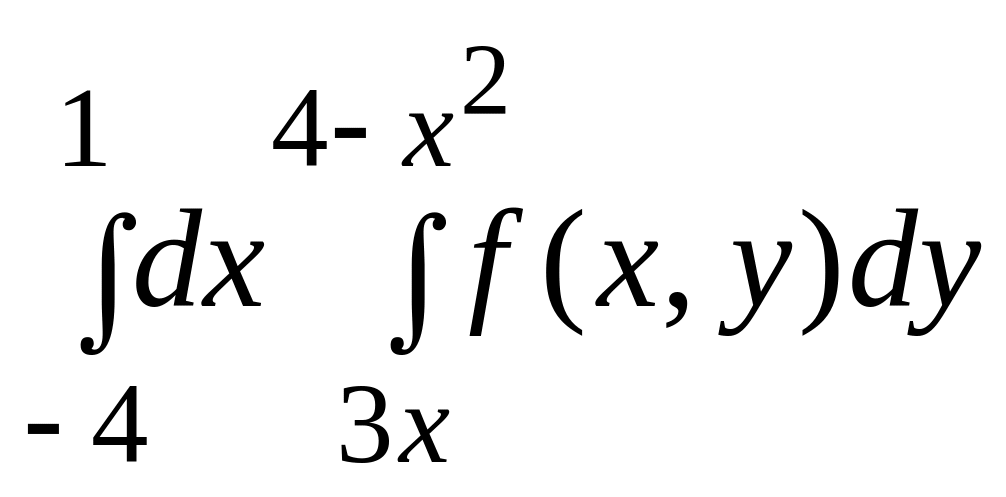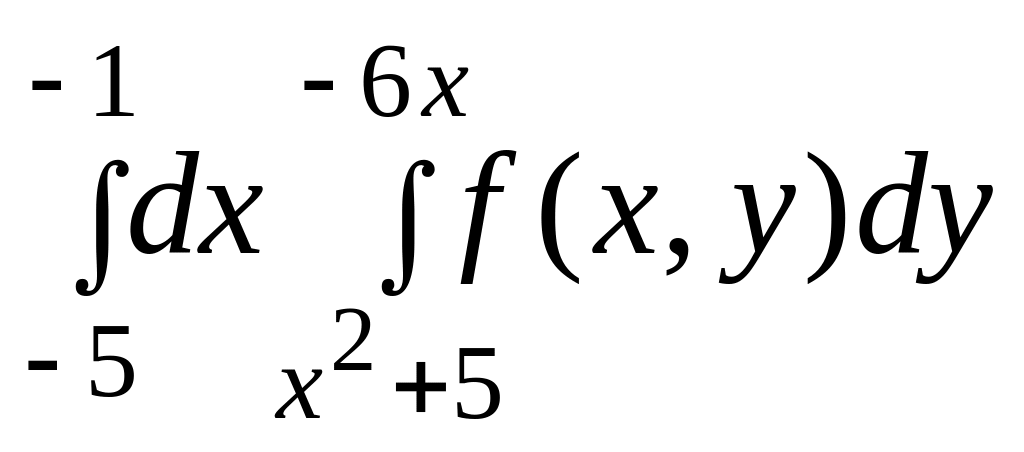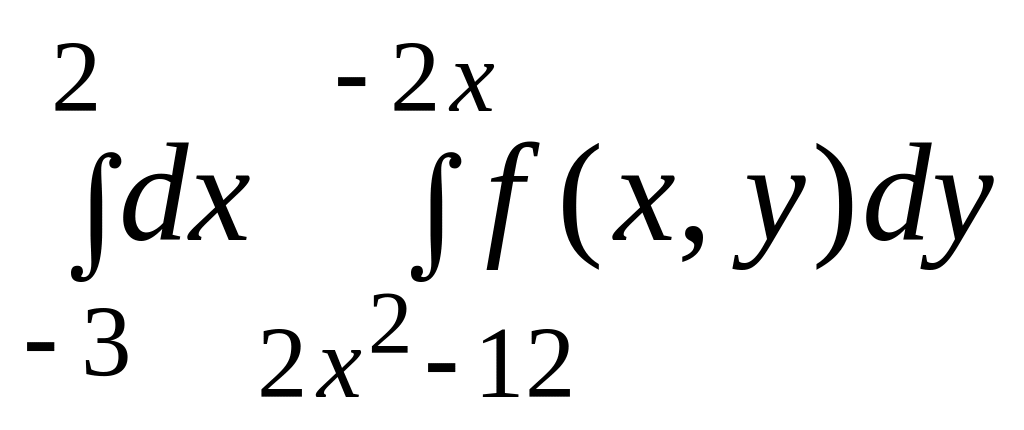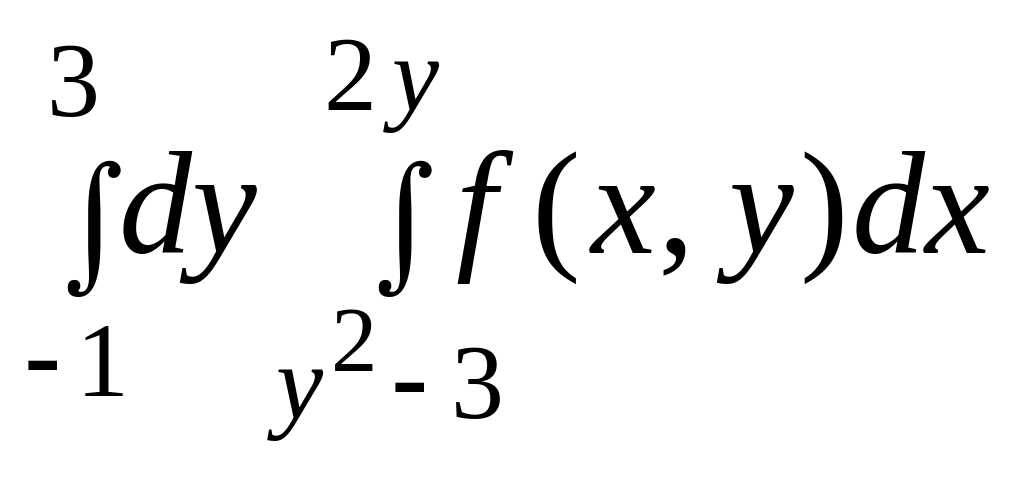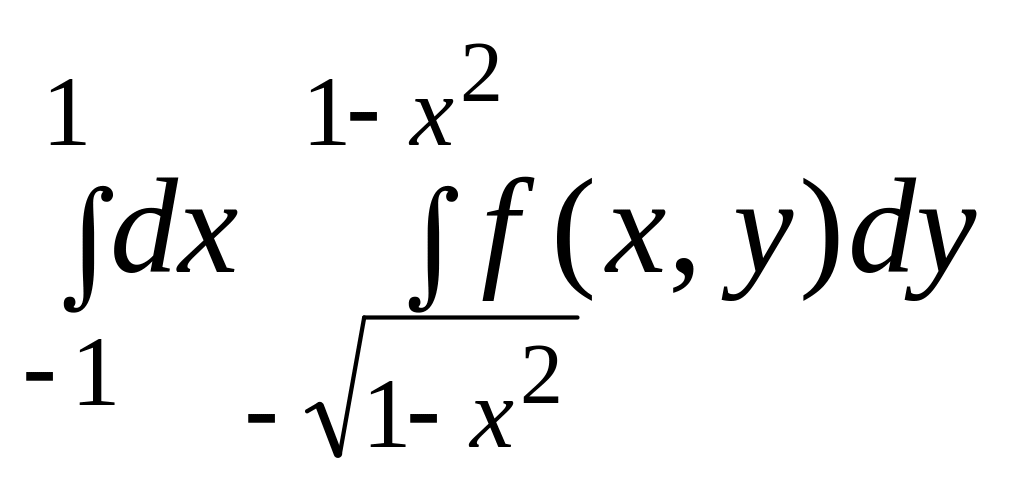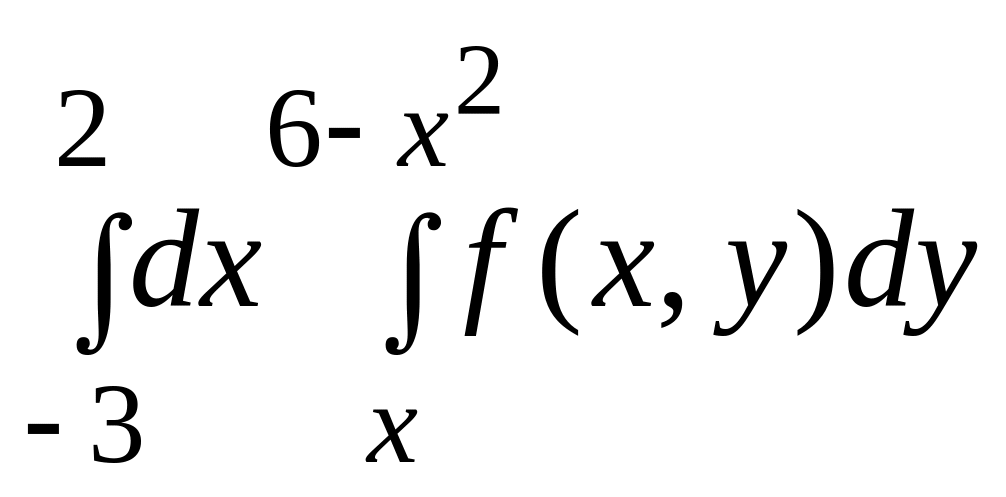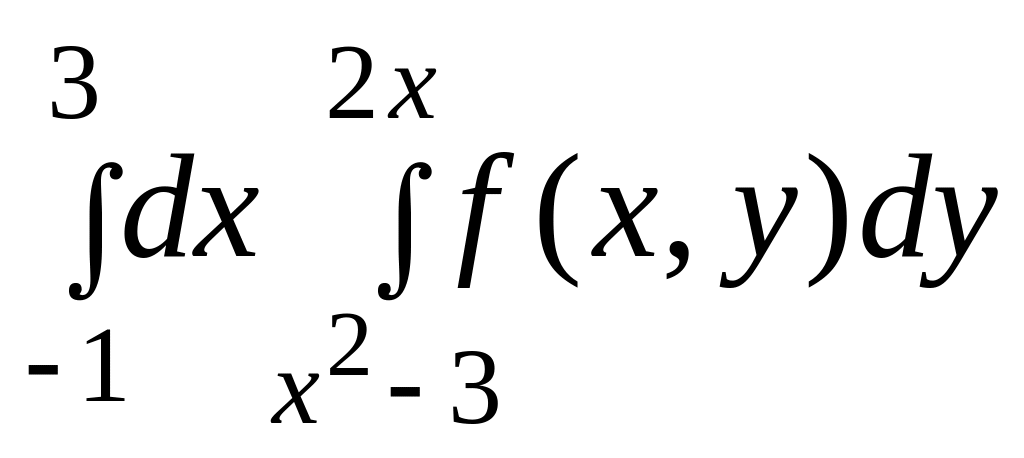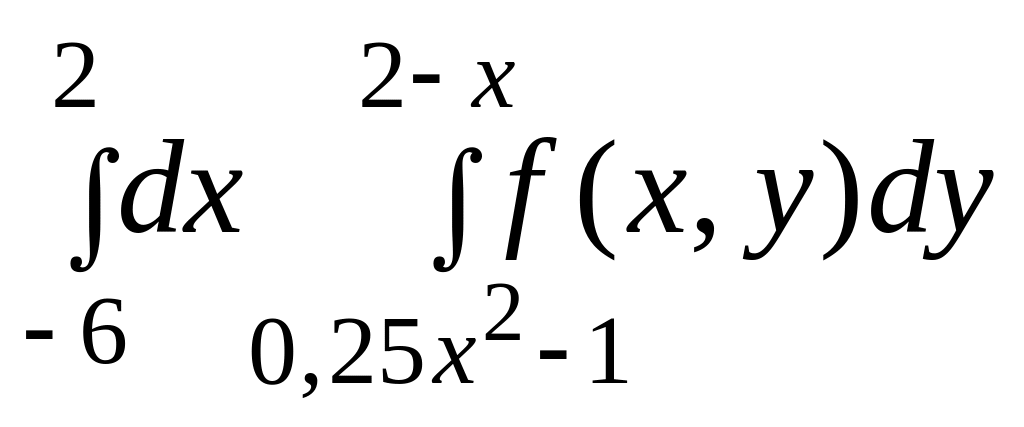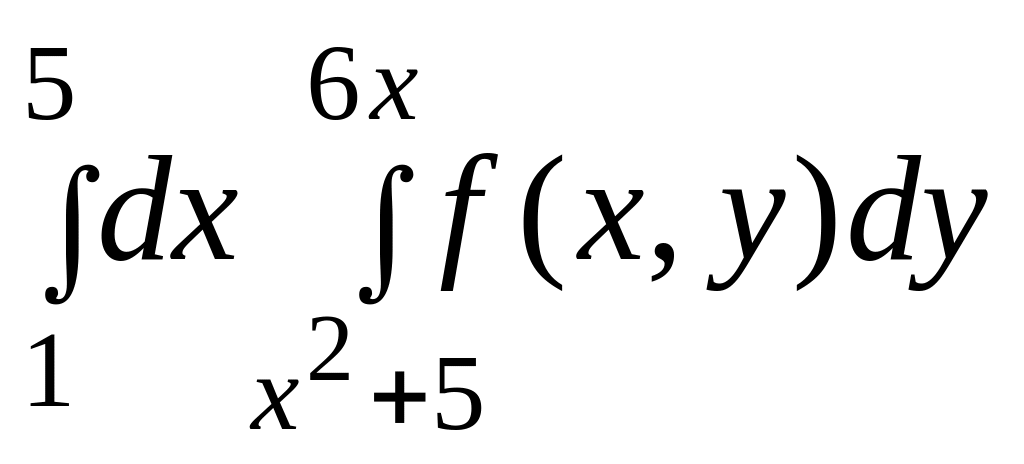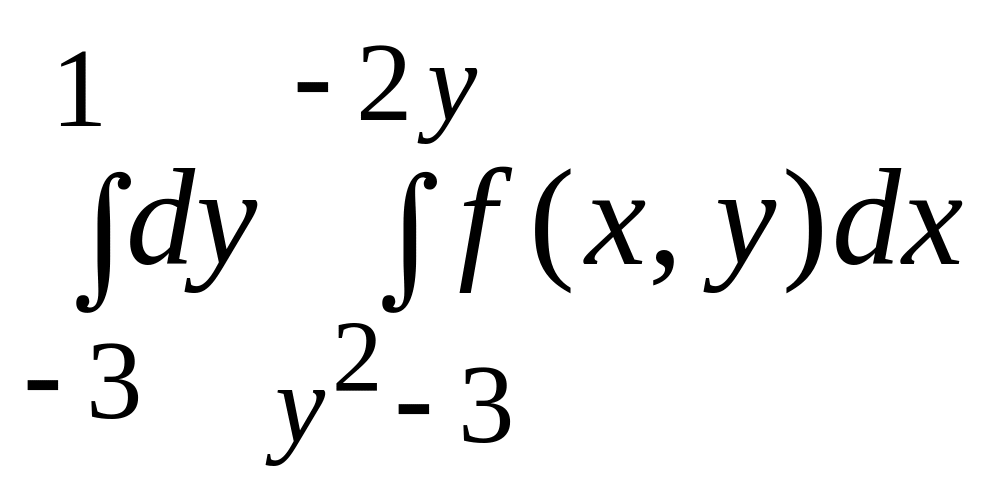Задание 6

Изменить порядок интегрирования в двойных интегралах:

1.	2.	3.
4.	5.	6.
7.	8.	9.
10.	11.	12.
13.	14.	15.
16.	17.	18. `
19.	20.	21.
22.	23.	24.
25.	26.	27.
28.	29.	30.
31.	32.	33.
34.	35.	36.
37.	38.	39.
40.

Задание 7

Найти общее решение дифференциальных уравнений первого порядка.

1. а) y = y/x + (y/x)²; б) (1+x²) y – 2xy = (1+x²)².

2. а) y = (2y – x)/y; б) y – 3x² y – x² = 0.

3. а) y = (y ln(y/x) + y)/x; б) x y + y – 3 = 0.

4. а) y = y/x + (y/x)³; б) y – 2y/(1+x) = (1+x)³.

5. а) y = y/x + x/y; б) y + (1–2x)y/x² –1 = 0.

6. а) y = y/x – 1/cos²(y/x); б) y + xy = x³y³.

7. а) y = ctg(y/x) + y/x; б) (1–x²) y – xy = 5xy².

8. а) y = (xy +y²)/(2x² +yx); б) y +y/x = (1+x)/y².

9. а) y = – y/x + (y/x)²; б) y – xy = xy².

10. а) y = tg(y/x) + y/x; б) xy = y(y ln x –2).

11. а) y = sin(y/x) + y/x; б) y–ycos x=y²cosx (1–sin x).

12. а) y = (x² +yx +y²)/x²; б) y +y/(x+1) +y² = 0.

13. а) y = y/x + (x/y)²; б) x y + y = y² ln x.

14. а) y = y(y³ + x³)/x⁴; б) y – y tgx = –y² cos x.

15. а) y = cos²(y/x) + y/x; б) y + 2y/x = 2 /cos² x.

16. а) xyy = y² + 2x²; б) y – y = –y² cos x.

17. а) y = (x² +y²)/(2xy); б) x y +4y – x² =0.

18. а) y = 2yx/((x² – y²) ; б) y = xy/(x²–1) +x .

19. а) y² + x² y = yx; б) x y + y = y².

20. а) y – y/x = (y³ + x³)/(xy²); б) y +y = e^3x y²/3.

21. а) (2x² +y²)dx –3xydy=0; б) x y =2y–x².

22. а) y = e^y/x + y/x; б) y + y tgx = –y² /cos² x.

23. а) xy = y ln(y/x); б) 2y – x/y = xy/(x²–1).

24. а) y = (y–x)/(y+x); б) y – y = e^x/x.

25. а) (xy – y) arctg(y/x) = x; б) y – y/x = 6 x^5/2 .

26. а) (y² –3x²)dy+2yxdx = 0; б) y= 3y/x +x⁴.

27. а) xy –y = x/arcsin(y/x); б) y + 2y/x = x³.

28. а) yx² = y² + xy; б) y = xy + .

1.29. а) y = y/x (1+ ln(y/x)); б) y + 2y(1–x²) = 1–x.

30. а) y = (x+y)/(y–x); б) y = x³y + .

31. а) y =(2y +x)/y; б) y + yx = .

32. а) yx² = x² + xy; б) y =y/sin x +2tg(x/2).

33. а) y = (x² – y²)/(yx); б) y = x²y + .

34. а) xy = y + x tg(y/x); б) y + 2y = 4x.

35. а) xy²y = x³ + y³; б) y +(1– 2x)y/x² = 1.

36. а) (2x²+xy) y = yx + y²; б) y +y = cos x.

37. а) (y³–xy²)dx + (x³– yx²)dy=0; б) y + 2xy = x .

38. а) xdy –ydx = ydy; б) y – y tg x = 1/cos x.

39. а) xy sin(y/x) +x= ysin(y/x); б) x y +y = e^x.

40. а) xy ln(y/x) =x + yln(y/x); б) xy – y/(x+1) = x.