1 Анализ существующих способов уравновешивания осевой силы в центробежных насосах
1.1 Оценка величины осевой силы, действующей на рабочее колесо
Во время работы центробежного насоса на его ротор действует сложная система сил. В случае применения в насосе рабочих колес одностороннего входа с проходным валом (рис. 1.1), среди действующих сил наибольшей по абсолютному значению будет являться осевая сила. Причина её возникновения – отсутствие симметрии рабочего колеса относительно плоскости перпендикулярной оси ротора. Площадь внешней поверхности основного диска, находящаяся под давлением нагнетания, больше аналогичной поверхности покрывающего диска, что приводит к возникновению статической силы давления, направленной в сторону входной воронки. Также, вдоль ротора действует динамическое усилие, вызванное изменением направления потока жидкости в рабочем колесе с осевого на радиальное, которое направлено в сторону нагнетания.
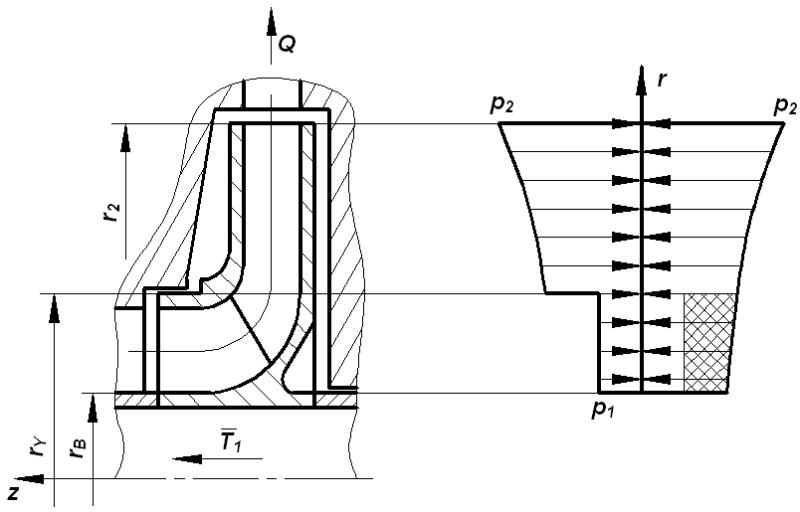
Рисунок 1.1 – Схема распределения давления
по боковым поверхностям рабочего колеса
При вычислении
величины осевой силы необходимо учесть,
что распределение давления по поверхностям
дисков рабочего колеса не постоянно, а
зависит от формы движения жидкости в
пазухах ступени. Основное влияние на
эпюру давления оказывает окружное
течение жидкости. Обычно при расчете
осевой силы предполагают, что вследствие
вязкости, жидкость, находящаяся в камерах
между дисками рабочего колеса и корпусом
ступени, вращается как твердое тело с
угловой скоростью
,
равной половине угловой скорости
вращения ротора
[ ]. В этом случае нахождение распределения
давления по поверхностям дисков рабочего
колеса сводится к решению задачи
относительного покоя жидкости во
вращающейся системе координат. При
равномерном вращении жидкости на её
элементарный объем действуют две
массовые силы: сила тяжести и центробежная
сила инерции. В центробежном насосе
угловая скорость ротора столь велика,
что силой тяжести можно пренебречь по
сравнению с центробежной силой. Тогда
дифференциальное уравнение гидростатики
будет иметь вид
. (1.1)
Из (1.1) путем интегрирования получим закон распределения давления, имеющий параболическую форму
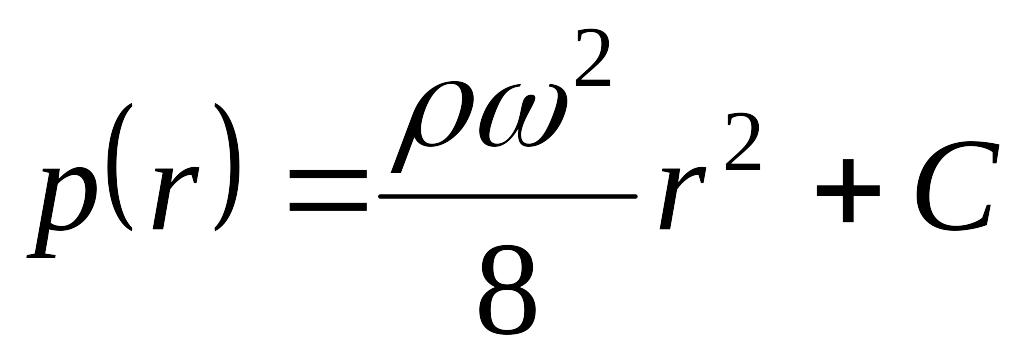. (1.2)
Постоянная
интегрирования
определяется из условия, что давление
на радиусе
равно давлению нагнетания
,
откуда
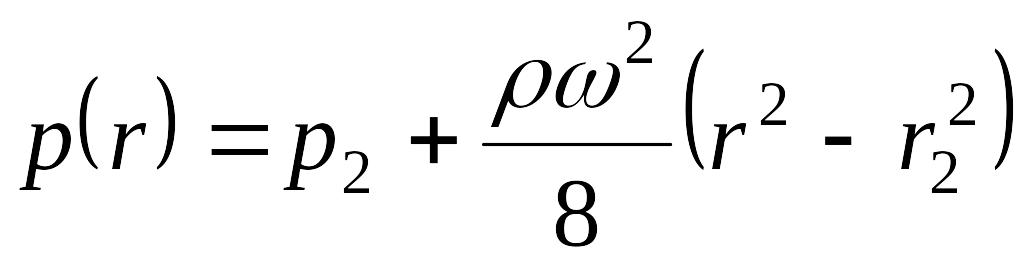. (1.3)
Согласно рис. 1.1
давление на боковых поверхностях,
ограниченных радиусами
и
,
взаимно уравновешивается. Статическая
составляющая осевой силы возникает под
действием неуравновешенной части
давления (заштрихованная область эпюры),
действующего на поверхность, ограниченную
радиусами
и
.
Величина этой силы определяется по
формуле [ ]
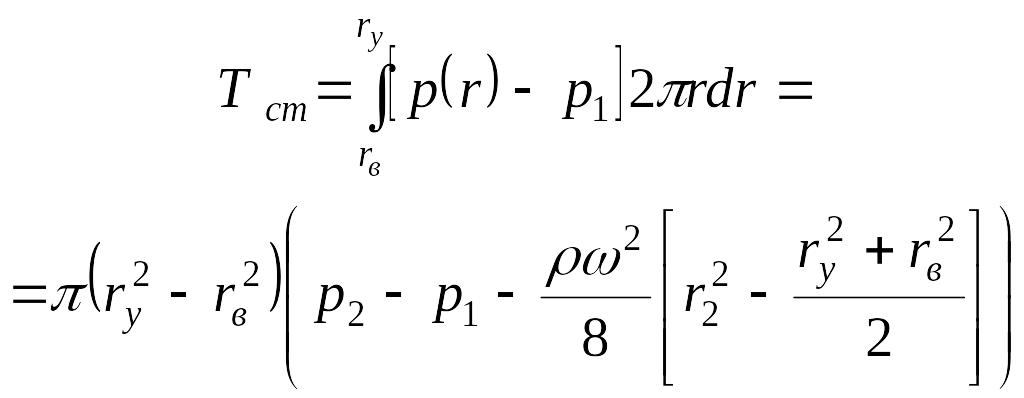. (1.4)
Во время работы насоса через уплотнения рабочего колеса происходит утечка жидкости, которая приводит к возникновению радиальных потоков в пазухах ступени. Радиальный поток в передней пазухе направлен к центру, что несколько увеличивает окружную скорость течения жидкости. Обратный эффект дает радиальный поток в задней пазухе, направленный к периферии. Таким образом, радиальные течения в камерах промежуточных ступеней насоса приводят к некоторому увеличению осевой силы по сравнению с расчетным значением [ ]. Однако в настоящее время величину осевой силы оценивают по формуле (1.4), основанной на законе распределения давления (1.3), предполагая, что при нормальных зазорах в уплотнениях утечки жидкости малы и ими можно пренебречь [ ]. Более точные методики расчета осевой силы с учетом радиальных течений жидкости предложены в работах [ ]. Эти методики основаны либо на численном интегрировании уравнений движения жидкости на ЭВМ [ ], либо на применении поправочных коэффициентов, полученных экспериментальным путем [ ].
Интерес представляет предельный случай аварийного износа переднего уплотнения ступени, допускающий аналитическое решение. В этом случае закон движения жидкости в передней пазухе ступени имеет вид [ ]
. (1.5)
Для рабочих колес
с
приближенно можно принять, что
[ ], тогда закон распределение давления
по диску будет следующим
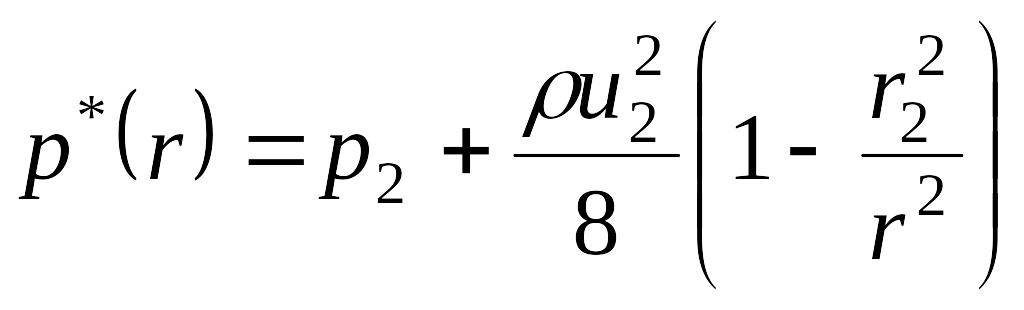, (1.6)
а дополнительная осевая сила, вызванная износом переднего уплотнения ступени будет равна [ ]
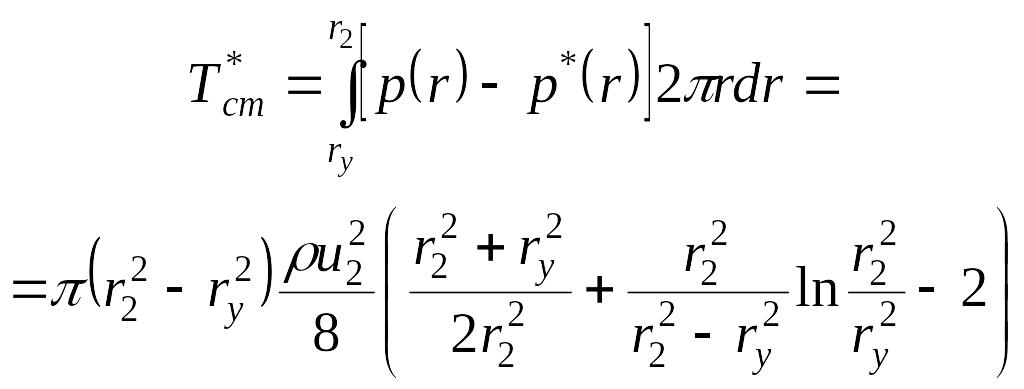. (1.7)
Величина динамической составляющей осевой силы определяется согласно закону изменения количества движения выражением [ ]
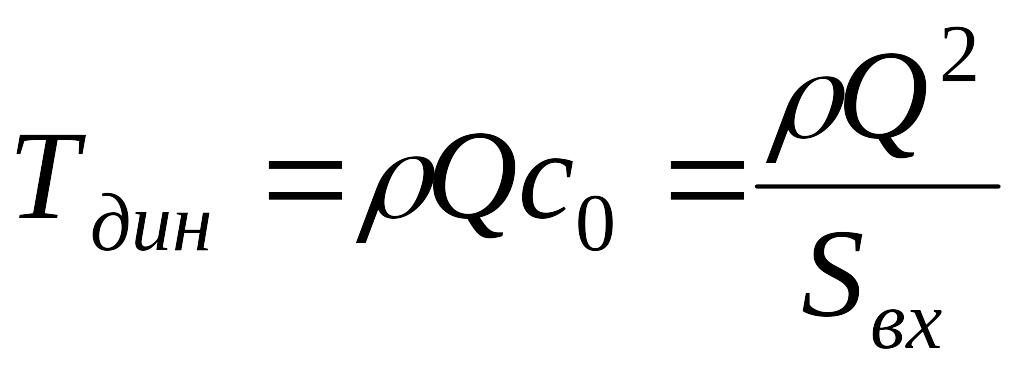. (1.8)
Численное значение
динамической составляющей ориентировочно
равно
[ ].
Разницу давлений
в формуле (1.4) можно выразить через
статический напор рабочего колеса
,
приведя её к виду
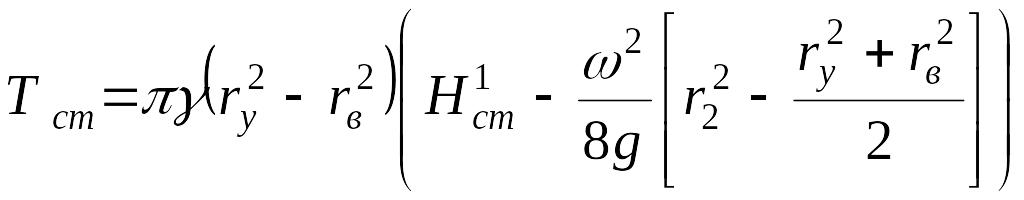. (1.9)
Таким образом, осевая сила, действующая на рабочее колесо при нормальных зазорах в уплотнении равна
. (1.10)
Осевая сила, действующая на рабочее колесо при аварийном износе переднего уплотнения ступени равна
. (1.11)
Осевая сила, действующая на ротор многоступенчатого насоса, равна сумме осевых усилий отдельных ступеней
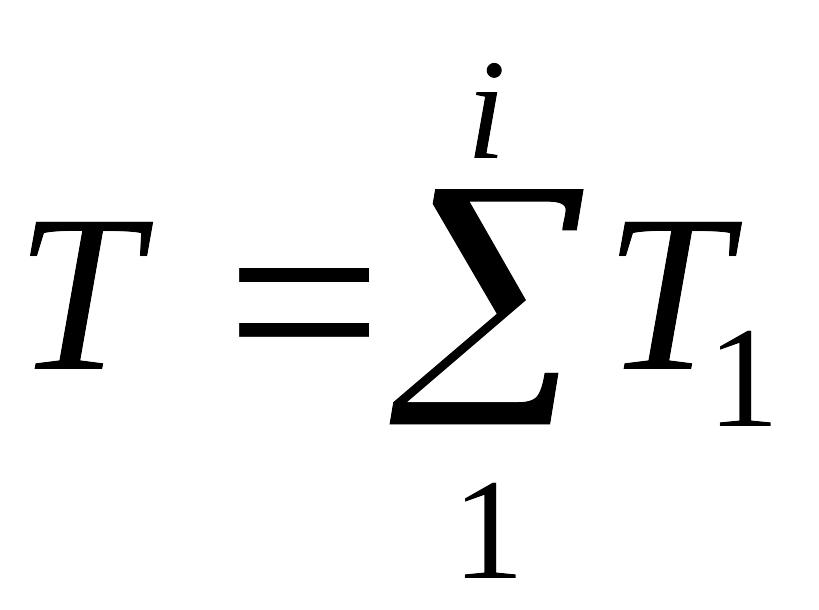. (1.12)