Лабораторная работа

Определение жесткости пружины и параметров затухания колебаний на пружинном маятнике

Цель работы: определение жесткости пружины статическим и динамическим методами, изучение затухающих колебаний на примере упругих колебаний пружинного маятника.

Оборудование: платформа на регулирующихся ножках, закрепленная на ней стойка со шкивом и угломерной шкалой на конце; закрепленные на платформе часы-таймер; пружина, наборный груз, две пластмассовые втулки, линейка с отверстием на конце, треугольник из пресс-картона с четырьмя отверстиями и крючком.

Теоретическое введение Затухающие колебания Уравнение затухающих колебаний

В любой реальной колебательной системе есть силы сопро­тивления (трения), действие которых приводит к уменьшению амплитуды и энергии колебаний. Такие свободные колебания называют затухающими.

Будем исходить из основного уравнения динамики, полагая, что на частицу массы т действует кроме квазиупругой силы (-kх) сила сопротивления, пропорциональная скорости части­цы (простейший, и вместе с тем наиболее часто встречающийся случай), , где r — коэффициент сопротивления (величина размерная). Тогда уравнение движения будет иметь вид

, (1)

или

, (2)

где 2β = r/m, . Отметим, что ω₀ — это частота свобод­ных колебаний без трения. Частоту ω₀ называют собственной частотой осциллятора, а β — коэффициентом затухания.

Уравнение (2) при условии β < ω₀ описывает затухающие колебания. Его решение, полученное с использованием средств математического анализа (теории линейных дифференциальных уравнений второго порядка), имеет вид:

, (3)

где a₀ и α — постоянные, определяемые начальными условия­ми x(0) = x₀ и ,

. (4)

Анализ выражения (4) показывает, что величина ω является частотой затухающих колебаний.

Г

Рисунок 1

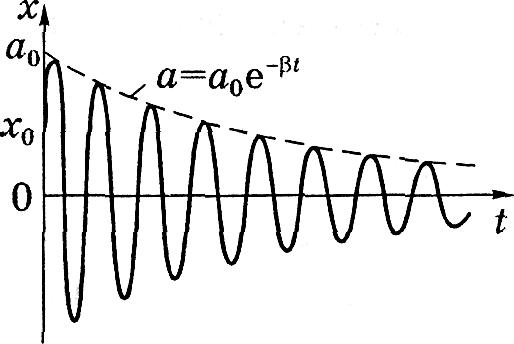
рафик функции (3) показан на рис. 1 для случая х₀ > 0 и . Затухающий колебательный процесс не является в строгом смысле пери­одическим. Действительно, рассмотрим момент времени t_n, когда cos(ωt_n + α) = 1 и следовательно x(t_n)=a(t_n)= . Ясно, что при любом t > t_n x(t) < x(t_n), т. е. значение функции x(t_n) не повторяется ни при каких t > t_n. Ясно в то же время, что благодаря гармоническому множителю cos(ωt + α) функция x(t) обладает определенной повторяемостью: в частности, повто­ряются через равные промежутки времени как нулевые значения функции x(t), так и ее максимумы и минимумы. Поэтому величину Т = 2π/ω принято называть периодом зату­хающих колебаний:

. (5)

Множитель а = а₀е^-βt перед косинусом в (3) называют ам­плитудой затухающих колебаний (пунктир на рис. 1).