I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ

Теория вероятностей - это математическая наука, изучающая закономерности в случайных событиях.

1. Основные понятия теории вероятностей. Алгебра случайных событий.

Случайное явление - это такое явление, которое при неоднократном воспроизведении одного и такого же опыта (испытания, эксперимента) протекает каждый раз несколько по иному.

Примеры случайных явлений: стрельба по цели; погода; продажа акций и др.

Случайным событием (далее просто событием) называется всякий факт, который в результате опыта может произойти или не произойти.

Примеры случайных событий:

1) опыт - бросание монеты; событие А - появление герба;

2) опыт - выстрел по мишени; событие B - попадание;

3) опыт - выявление спроса покупателей на какой-то товар; событие D - не менее 25% покупателей этот товар оценивают положительно.

Несколько событий в данном опыте образуют полную группу событий , если в результате опыта должно появиться хотя бы одно из них.

Примеры событий, образующих полную группу:

1) курс акций на следующей неделе "упадет", "возрастет", "останется прежним";

2) появление "1", "2", "3", "4", "5", "6" при бросании игральной кости;

Несколько событий в данном опыте называются несовместными, если никакие из них не могут появиться вместе.

Примеры несовместных событий:

1) "появление туза" и "появление десятки" при вынимании одной карты из колоды;

2) "покупательный спрос на -ый товар" возрастает и "покупательский спрос на N-ый товар" уменьшится.

Изображая случайное событие геометрическим множеством точек области , то несовместные события A и B изобразятся непересекающимися подмножествами ( рис.1 )

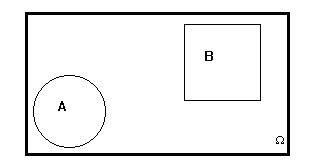
Несколько событий в данном опыте называются совместными, если хотя бы два из них могут произойти одновременно (рис. 2)

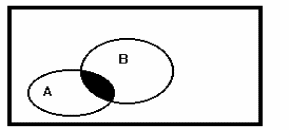
Событие А называют следствием события В (В А), если из появления события В следует появления события А (рис.3)

Рис.3

Каждый из возможных взаимоисключающих исходов опыта называют элементарным (неразложимым) событием. Из элементарных событий можно образовать составные (разложимые) события. Событие С называется составным, если можно указать по крайней мере два таких элементарных события и , что из осуществления каждого из них в отдельности следует факт осуществления события С.

Пример: событие С "выпадение четного числа очков при однократном бросании игральной кости" - состоит из трех элементарных событий: "выпало 2", "выпало 4", "выпало 6".

Элементарные события, входящие в состав составного события, называются благоприятствующими.

Равновозможными событиями в данном опыте являются такие события, что по условиям симметрии есть основания считать, что ни одно из них не является объективно более возможным, чем другое.

Пример: выпадение каждой грани игральной кости.

Достоверное событие определяется как событие, состоящее из всех возможных элементарных событий, т.е. в результате анализируемого случайного эксперимента обязательно произойдет одно из элементарных событий , I=1,2, ... , а следовательно, тот факт, что событие произойдет, достоверно.

Невозможное (пустое) событие - это событие, не содержащее ни одного элементарного события и, следовательно, при реализации исследуемого случайного эксперимента его осуществление невозможно.

В теории вероятностей над событиями производят различные операции, тесно связанные с алгеброй логики. Основными операциями являются сумма (объединение), произведение (пересечение), разность и взятие дополнения.

Суммой или объединением событий А1, А2, ... Аn называется такое событие С ( С= или С= ), которое состоит в осуществлении хотя бы одного из этих событий. Геометрическая интерпретация суммы событий показано на рис.4

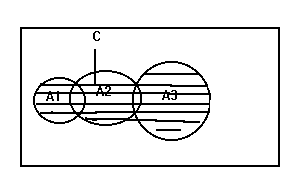
Рис.4

Пример: если опыт состоит из трех выстрелов по мишени, и даны события: "А0 - ни одного попадания", "А1 - ровно одно попадание", "А2 - ровно два попадания", "А3 - ровно три попадания", то С=А0+А1+А2 - есть событие "не более двух попаданий"; В=А2+А3 - "не менее двух попаданий".

Произведением или пересечением событий А1, А2, ... , Аn называется такое событие С ( С= ), которое состоит в обязательном совместном наступлении всех событий А1, А2, ... Аn. Геометрическая интерпретация произведения событий показано на рис.5.

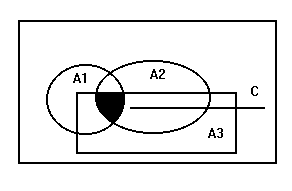
Рис.5

На языке элементарных событий произведение событий А1, А2, ... , Аn определяется как событие С , состоящее только из тех элементарных событий, которые одновременно входят во все рассматриваемые события.

Пример: покупается три лотерейных билета и рассматриваются события "В1 - первый билет без выигрыша", "В2 - второй билет без выигрыша", "В3 - третий билет без выигрыша", то событие В=В1В2В3 состоит в том, все три билета окажутся без выигрыша.

Операции сложения и произведения над событиями обладают рядом свойств, аналогичных свойствам обычных сложения и умножения чисел:

1. Переместительное свойство:

А+В=В+А; А*В=В*А.

2. Сочетательное свойство:

(А+В)+С=А+(В+С); (А*В)*С=А*(В*С).

3. Распределительное свойство:

А*(В+С)=А*В+А*С.

Однако некоторые операции над событиями не равнозначны операциям над числами, в частности, для событий

А+А=А; А*А=А.

Разностью событий А и В называется событие С (С=А-В), состоящие в том что событие В не происходит. Геометрическая интерпретация разности событий показано на р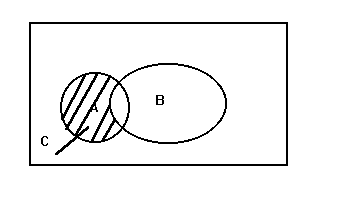ис.6

рис.6

Событие = называется дополнением к А или противоположным А (р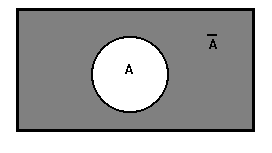ис.7).

рис.7

Очевидно, что - это невозможное событие, а противоположные события А и представляют собой простейший случай полной группы событий.

Составные события можно представить в виде комбинаций элементарных или более простых событий, применяя рассмотренные выше операции.

Пример: при вытягивании трех лотерейных билетов возможны следующие элементарные события:

А1, А2, А3 - выигрыш первого, второго, третьего билета, соответственно;

, - проигрыш первого, второго, третьего билета, соответственно.

Рассмотрим составное событие В, состоящие в том, что из трех билетов только один может оказаться выигрышным. Очевидно, что событие В можно представить в следующей комбинации:

В=

Из определения суммы, произведения, разности, дополнения событий и их свойств вытекают следующие формулы:

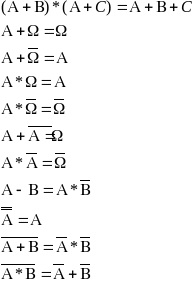
Используя эти формулы, которые легко проверяются самостоятельно, можно представлять составные события в более простом аналитическом виде.

Выводы:

1. Понятиями теории вероятностей являются случайное явление; случайное событие, полная группа событий, элементарное событие, составное событие, несовместимые события, совместимые события, достоверное событие, невозможное событие, противоположное событие, равновозможные события.

2. Основными операциями над случайными событиями являются сумма (объединение), произведение (пересечение), разность и дополнение.

3. Любое составное событие можно представить в виде комбинаций элементарных событий или более простых событий.

Основные теоремы теории вероятностей

Вероятность случайного события

Одной из важнейших характеристик случайного события является его вероятность, которую в большинстве практических задач связывают с эмпирическим понятием частоты события.

Частотой Р события А в данной серии испытаний называется отношение числа испытаний m, в которых появилось данное событие, к общему числу испытаний n:

Частота событий обладает следующими свойствами:

1. Частота случайного события А есть неотрицательное число, заключенное между нулем и единицей:

2. Частота достоверного события равна единице.

3. Частота невозможного события равна нулю.

4. Частота суммы двух несовместных событий А и В равна сумме частот этих событий:

5. Частота произведения двух событий равна произведению частоты одного из них на условную частоту другого.

Условной частотой называют частоту одного события, вычисленную при условии наступления другого события, обозначают Следовательно,

Вероятностью события А называется постоянное число, около которого группируются частоты этого события по мере увеличения количества опытов (статистическое определение вероятности события).

При небольшом числе опытов, частота события носит в значительной мере случайный характер. Пусть, например, опыт - бросание монеты, событие А - "появление герба". На рис.7 изображена зависимость появление герба от числа опытов n (логарифмическая шкала по оси абсцисс).

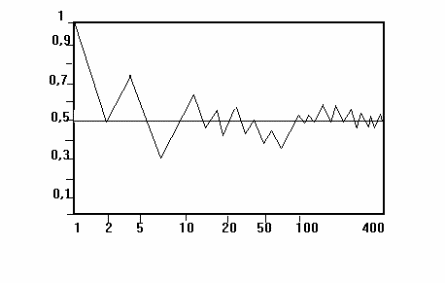
рис.7

Из рис.7 видно, что по мере увеличения n частота проявляет тенденцию стабилизироваться, приближаясь сквозь ряд случайных отклонений к постоянной величине, равной 0,5 (это и есть вероятность появление герба в одном опыте).

Хотя вероятность события в самой своей основе связана с опытным, практическим понятием частоты события, однако для ее определения не всегда есть возможность провести большое число опытов.

Если пространство , связанное с опытом, состоит из конечного числа равновозможных элементарных событий то вероятность любого случайного события А в таком опыте равна отношению числа m благоприятствующих ему элементарных событий к их общему числу n (классическое определение вероятности событий):

Если пространство содержит бесконечное множество элементарных событий, то может быть использовано геометрическое определение вероятности, когда вероятность попадания точки в любую область пропорциональна мере этой части (длине, площади, объему) и не зависит от ее расположения и формы.

Если геометрическая мера всей области S, а геометрическая мера части этой области, попадание в которую благоприятствует данному событию А, есть , , то вероятность события

В общем случае, когда множество элементарных событий является непрерывным, строится аксиоматическая теория вероятностей.

При этом для того, чтобы теория вероятностей хорошо согласовалась с опытом, аксиомы теории вероятностей вводятся таким образом, чтобы вероятность события обладала основными свойствами частоты события.

Вероятностью события Р(А) события А называется определенная на действительная функция, удовлетворяющая трем аксиомам:

Аксиома 1. Вероятность события А есть неотрицательное число:

Аксиома 2. Вероятность достоверного события равна единице:

Аксиома 3. Вероятность суммы попарно несовместных событий равна сумме вероятностей этих событий:

Из аксиом 1, 2, 3 следует, что в частности, вероятность невозможного события равно нулю. Важно отметить, что непрерывном вероятном пространстве из равенств Р(А)=1 или Р(А)=0 не следует, что А является достоверным или соответственно невозможным событием. Из аксиомы 3 следует связь между вероятностями прямого или противоположного событий:

Вводимая далее аксиома 4 определяет условную вероятность.

Аксиома 4. Условная вероятность Р(А/В) события А при условии, что уже имеет место событие В, определяется с помощью формулы:

Р(АВ)=Р(В)*Р(А/В)=Р(А)*Р(В/А).

Два события А и В называются зависимыми, если вероятность каждого из них меняется в связи с наступлением или не наступлением другого. В противном случае события А и В называются независимыми.

Вероятность произведения двух независимых событий равна произведению этих событий:

Р(АВ)=Р(А)*Р(В).

Задачи на вычисление частоты событий и их вероятностей.

Задача 1. Среди 250 изготовленных деталей оказалось пять, не отвечающих стандарту. Определить частоту появления деталей, не отвечающих стандарту.

РЕШЕНИЕ: Из определения частоты получаем, что

Задача 2. Среди 25 студентов группы, в которой десять девушек, разыгрывается пять билетов . Определить вероятность того, что среди обладателей окажутся две девушки.

РЕШЕНИЕ: Число всех равновозможных случаев распределить пять билетов среди 25 студентов равно числу сочетаний Число групп по трое юношей из 15, которые могут получить билеты, равно С . Каждая такая тройка может сочетаться с любой парой из десяти девушек, а число таких пар равно С . Таким образом, число групп по пять студентов, в каждую из которых будут входить трое юношей и две девушки, равно произведению Это произведение равно числу благоприятствующих рассматриваемому событию случаев. Из классического определения вероятности события, получаем:

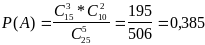
Задача 3. В любые моменты интервала времени Т равновозможны поступления двух телефонных звонков. Абонент не сумеет ответить на оба звонка, если разность между моментами поступления сигналов будет меньше . Определить вероятность Р(А) того, что абонент не сумеет ответить на оба звонка.

РЕШЕНИЕ: Изобразим случайные моменты поступления звонков в виде декартовых координатах на плоскости. Областью возможных значений является квадрат площадью (рис.8). Абонент не сумеет ответить на два звонка, если

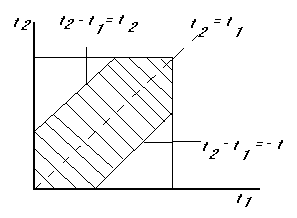
Рис. 8

Данная область лежит между прямыми Площадь этой области Используя геометрическое определение вероятности, получаем:

При определении вероятности составных событий используют основные теоремы теории вероятностей, являющиеся следствием приведенных выше аксиом и определений.