ФГБОУ ВПО «Тверская государственная сельскохозяйственная академия»

Кафедра «Физики, механики и инженерной графики»

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

КИНЕМАТИКА

Методические указания для выполнения контрольной работы

студентами зочного отделения инженерного факультета

Тверь 2014

Ю.В. Елисеев

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА

КИНЕМАТИКА

Методические указания для выполнения контрольной работы

студентами зочного отделения инженерного факультета

Рецензент:

доцент кафедры сельскохозяйственные машины Сафонов В.В.

Рекомендовано к изданию на заседании кафедры физики:

Протокол №5 от 13 . 01. 2014г.

Рекомендовано к изданию методической комиссией инженерного

факультета :

Протокол №4 от 15 .01. 2014г.

Глава 2. Кинематика

§ 1. Краткие сведения из теории

Кинематика точки

Кинематикой называется раздел механики, в котором изучается движение тел без учета причин, вызывающих это движение.

Механика изучает простейшую форму движения - механическое движение. Под механическим движением понимается изменение с течением времени относительного положения материальных тел.

Основная задача кинематики состоит в том, чтобы, зная закон движения данного тела (или точки), определить все кинематические величины, характеризующие как движение тела в целом, так и движение каждой его точки в отдельности.

Изучение кинематики следует начать с изучения движения точки (кинематики точки), а затем перейти к изучению кинематики твердого тела. Линия, описываемая движущейся точкой в пространстве, называется траекторией точки. По видутраектории движения точки делятся на криволинейные и прямолинейные.

Способы задания движения точки

Движение точки относительно выбранной системы отсчета будет задано, если в любой момент времени t будет известно положение точки в этой системе отсчета.

Существует три способа задания движения точки:

1) естественный;

2) координатный;

3) векторный.

1.Естественный способ

Чтобы задать движение точки естественным способом, нужно задать:

1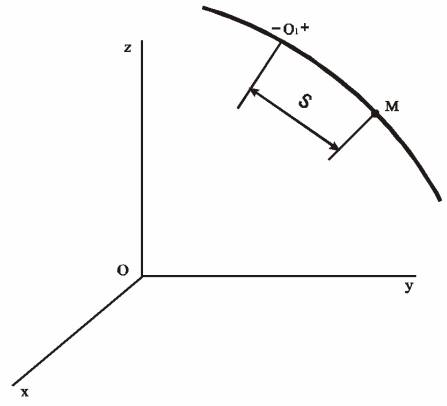 ) траекторию точки М относительно системы отсчета oxyz (рис. 1);

2) начало отсчета на траектории (т. O₁) с указанием положительного направления отсчета;

3) закон движения точки вдоль траектории в виде S =f(t), где S - дуговая координата точки, которая однозначно определяет положение точки М на траектории. Величина S определяет положение точки М на траектории, а не

Рис. 1 пройденный путь.

2. Координатный способ

При этом способе положение движущейся точки определяется ее прямоугольными декартовыми координатами х, у, z, при движении все три координаты будут меняться с течением времени.

Зависимости

(1)

э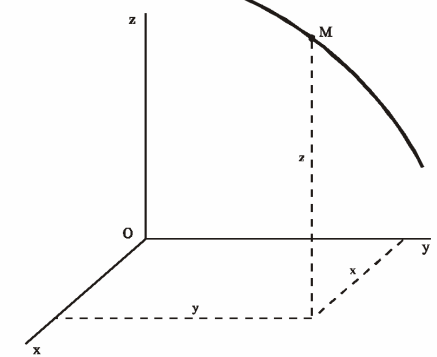 тих координат от времени и представляют собой уравнения движения точки в декартовых осях координат (рис. 2).

Уравнения (1) являются одновременно и уравнением траектории точки в параметрическом виде, если за параметр принять время t.

Исключив из уравнений движения время t, можно получить равнение траектории точки в обычной форме.

Рис.2

Определение скорости и ускорения точки при координатном способе задания ее движения

1. Определение скорости точки.

Пусть движение точки задано в декартовой системе координат уравнениями:

На основании формулы (4) получаем:

где V_x, V_y, V_z- -проекции скорости V на оси координат.

Проекции скорости на оси координат равны первым производным от соответствующих координат движущейся точки по времени.

Зная проекции скорости, легко определить ее модуль и направление.

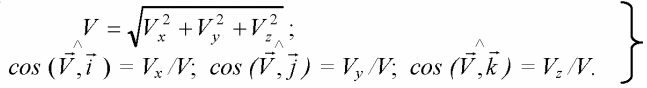
2. Определение ускорения точки.

На основании формулы (5) вектор ускорения точки

где a_х, a_y, a_z - проекции ускорения а на оси координат х, у, z.

Проекции ускорения на оси координат равны первым производным от проекций скоростей или вторым производным от соответствующих координат движущейся точки по времени.

Модуль и направление ускорения определяются по формулам: