Задача-эталон n4. Определение средней ошибки средней арифметической и доверительных границ средней величины
Используем среднюю арифметическую, полученную при решении задачи-эталона N1 и среднее квадратическое отклонение, рассчитанное в задаче-эталоне N3. Необходимо определить ошибку репрезентативности и доверительные границы средней величины. Средняя длительность лечения 37 больных ангиной составила 10.8 дней).
М = 108.8 |
σ = 2.7 |
n = 37 |
а) для расчета ошибки репрезентативности используем формулу:
m
=
=
=
=
0.4
дня.
в) доверительные границы вычисляем по формуле:
Mген. = Мвыб. tm
при Р = 95%, t = 2,
Мген. = 10.8 2×0.4 = 10.8 0.8 = 10 ÷ 11.6 (дней)
Следовательно, с вероятностью безошибочного прогноза, равной 95% можно утверждать, что в генеральной совокупности средняя длительность лечения больных ангиной будет находиться в пределах от 10 до 11.6 дней,
при Р = 99%, t = 3,
Мген. = 10.8 3×0.4 = 10.8 1.2 = 9.6 ÷ 12 (дней)
Следовательно, с вероятностью безошибочного прогноза равной 99% можно утверждать, что в генеральной совокупности средняя длительность леченая больных ангиной будет находиться в пределах от 9.6 до 12 дней.
Задача-эталон n5. Определение достоверности различий между двумя средними величинами
Требуется определить, имеется ли достоверное снижение частоты пульса и приближение ее к норме в группе студентов после экзаменов, если известно, что средняя частота пульса (М1) до экзамена составила 98.8 удара в минуту (m1=4 уд/мин); после экзамена (М2) -84 удара в минуту (m2 = 5 уд/мин).
Достоверность разности между средними величинами определяется по формуле:
t
=
=
=
=
=
2.3
поскольку t > 2, с вероятностью безошибочного прогноза свыше 95% можно утверждать, что после экзамена частота пульса у студентов снижается и приближается к норме.
Задача-эталон n6. Оценка достоверности различий двух относительных величин
Оценить эффективность иммунизации против гриппа, если известно, что в группе иммунизированных (150 чел.) заболело 42%, в группе, неиммунизированных против гриппа (200 чел.) заболело 48%.
Рассчитываем средние ошибки относительных величин по формуле:
m =
Достоверность различий относительных величин определяем по формуле:
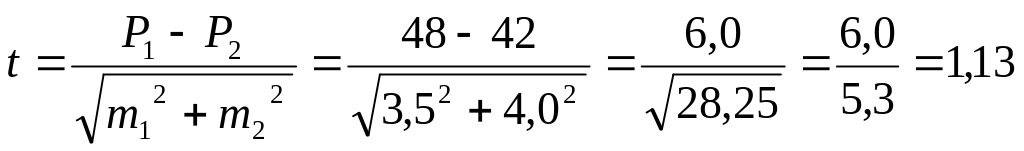
Поскольку t<2, следовательно, отсутствуют достоверные различия между показателями заболеваемости в группах иммунизированных и неиммунизированных, что говорит о неэффективности иммунизации против гриппа.
Варианты задач для самостоятельного решения
(построить вариационный ряд и определить моду, медиану, среднюю арифметическую, оценить вариабельность признака и достоверность полученной средней арифметической).
Рост 45 мальчиков в возрасте 2-х лет (в см): 89, 92, 93, 98, 92, 94, 91, 88, 94, 95, 93, 92, 91, 92, 82, 91, 92, 95, 88, 92, 91, 89, 93, 92, 94, 89, 90, 95, 88, 90, 83, 89, 90, 94, 96, 95, 93, 88, 98, 98, 94, 91, 90,94,93.
Сроки стационарного лечения 35 больных детей (в днях): 12, 20, 11, 14, 24, 15, 18, 20, 23, 25, 22, 24, 14, 16, 25, 13, 15, 18, 22, 19, 23, 29, 21, 24, 23, 18, 16, 15, 19, 20, 19, 21, 20, 23, 24.
Длина тела у 32 новорожденных мальчиков (в см): 49, 52, 54, 49, 52, 54, 50, 49, 53, 52, 54, 50, 50, 54, 49, 51, 51, 53, 51, 52, 53, 48, 48, 55, 56, 55, 49, 53, 52, 52, 50, 51.
Число больных НЗЛ, состоящих на диспансерном учёте у 45 участковых терапевтов: 8, 12, 16, 14, 15, 20, 21, 19, 12, 14, 21, 19, 13, 11, 7, 12, 6, 19, 10, 12, 14, 16, 15, 17, 18, 19, 21, 20, 22, 18, 13, 24, 19, 18, 21, 24, 21, 23, 25, 12, 14, 17, 15, 16, 17.
Длительность стационарного лечения больных острой пневмонией у 39 больных (в днях): 19, 20, 28, 21, 21, 27, 25, 21, 20, 20, 21, 23, 25, 24, 24, 20, 20, 21, 24, 19, 20, 19, 19, 21, 21, 20, 19, 18, 20, 20, 20, 21, 20, 20, 19, 21, 22, 25, 21.
Рост 41 девушек - студенток (см.): 174, 163, 168, 168, 161, 164, 164, 159, 160, 168, 172, 169, 164, 166, 169, 168, 172, 159, 165, 156, 169, 160, 161, 162, 162, 164, 172, 159, 163, 159, 162, 163, 172, 170, 168, 170, 159, 163, 162, 173, 169.
Частота сердечных заболеваний у 37 студентов (число уд/мин): 68, 80, 46, 70, 70, 74, 76, 80, 82, 86, 66, 68, 70, 76, 74, 72, 72, 70, 70, 76, 74, 66, 64, 68, 70, 68, 72, 80, 78, 52, 94, 68, 98, 96, 84, 80, 86.
Результаты измерения систолического артериального давления (в мм.рт.ст.) у 32 детей, страдающих нефропатиями: 125, 130, 110, 110, 115, 120, 95, 100, 110, 110, 125, 120, 135, 135, 120, 140, 120, 145, 130, 135, 115, 95, 125, 125, 130, 150, 140, 136, 125, 130, 125, 120.
Число диспансерных больных, состоящих на учете у 34 терапевтов составило: 150, 110, 105, 160, 170, 185, 165, 150, 155, 140, 125, 130, 115, 105, 125, 130, 145, 150, 140, 140, 160, 155, 145, 135, 145, 120, 120, 115, 125, 130, 140, 110, 115, 170.
Частота дыхания у 37 мужчин (число дыхательных движений в минуту): 12, 14, 16, 17, 20, 15, 14, 13, 16, 17, 17, 16, 16, 14, 13, 14, 12, 15, 16, 20, 21, 19, 17, 18, 16, 16, 17, 17, 18, 17, 17, 18, 20, 15, 13, 14, 17.
Длительность трудопотерь в связи с обострениями язвенной болезни у 32 больных составила (в днях): 21, 32 ,40, 34, 21, 23, 42, 37, 36, 28, 32, 41, 22, 20, 28, 27, 24, 29, 30, 30, 32, 29, 26, 34, 49, 43, 29, 24, 27, 25, 39, 28.
Результаты измерения массы тела 33 новорожденных мальчиков (в кг): 4.0, 3.2, 3.5, 4.4, 4.5, 3.0, 4.3, 3.8, 4.2, 3.3, 2.5, 4.2, 4.3, 3.7, 3.8, 4.2, 3.3, 3.1, 4.2, 3.5, 3.9, 3.2, 3.4, 3.8, 3.5, 3.9, 4.0, 4.2, 4.3, 4.0, 2.9, 3.1, 3.5.
Длительность лечения в ЦРБ 43 больных язвенной болезнью желудка составила в днях: 30, 25, 26, 29, 28, 29, 30, 24, 26, 25, 30, 30, 29, 30, 31, 33, 30, 29, 29, 25, 27, 27, 26, 34, 35, 29, 36, 30, 30, 30, 29, 26, 27, 27, 30, 30, 27, 32, 33, 24, 24, 28, 24, 35, 28.
Длительность одного случая нетрудоспособности рабочих в связи с ОРЗ и гриппом составила: 6, 6, 10, 11, 8, 7, 5, 6, 7, 8, 10, 12, 4, 5, 8, 5, 7, 9, 9, 4, 7, 5, 8, 10, 6, 5, 7, 8, 6, 7, 7, 8, 6, 5, 6, 7, 7, 8, 9, 6, 7.
Частота пульса у детей составила: 75, 80, 90, 85, 80, 70, 80, 95, 80, 85, 85, 75, 75, 80, 75, 90, 65, 75, 80, 70, 70, 65, 70, 65, 65, 65, 85, 80, 80, 85, 75, 85, 75, 65, 70.