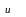Министерство образования и науки Российской федерации

Государственное образовательное учреждение

высшего профессионального образования

Казанский национальный исследовательский технический университет им. А.Н. Туполева

(КНИТУ – КАИ)

________________________________________________________________

Кафедра радиоэлектроники и информационно-измерительной техники

Изучение основных измерительных приборов

и измерение основных параметров сигналов и цепей

Методическое пособие к лабораторной работе №401

по дисциплине Электротехника и электроника

Авторсоставитель: Погодин Д.В.

Казань - 2012 г.

Цель работы  изучение основных характеристик и порядок работы с контрольно–измерительными приборами (генератором, осциллографом и цифровым мультиметром) при измерении основных параметров сигналов и цепей.

1. Основные понятия и расчетные соотношения

1. Основные параметры сигналов и цепей

1.1. Основные параметры сигналов

В электротехнике простейшим переменным сигналом является гармонический (ЭДС - е(t), напряжение - (u(t), ток - i(t)). Аналитически гармонический сигнал (например, напряжение) записывается выражением:

u(t) = U_mcos(ω₀t+φ₀) , (1.1)

где u(t) – мгновенное значение напряжения – напряжение в момент времени t.

Временная диаграмма гармонического сигнала приведена на рис.1.1. Он характеризуется следующими тремя основными параметрами:

1. u_m – амплитуда, величина наибольшего отклонения от нуля, (В- вольт);

2. Т – период, наименьший интервал времени, по истечении которого мгновенные величины повторяются, измеряется в (сек), с ним связаны f=1/Т – циклическая частота, измеряется в (Гц) и ω₀ =2πf – угловая частота - (рад/с);

3. φ₀ – начальная фаза, (рад). Выражение в скобках - (ω₀t+φ₀)= ψ(t) называют полная фаза. Отсюда φ₀ = ψ(t=0).

Рис.1.1. Временная диаграмма г армонического сигнала

Рис. 1.2. Временные диаграммы двух гармонических сигналов

Кроме амплитуд о величине периодических сигналов судят по их среднеквадратичным (действующим) значениям за период, I, U, E –

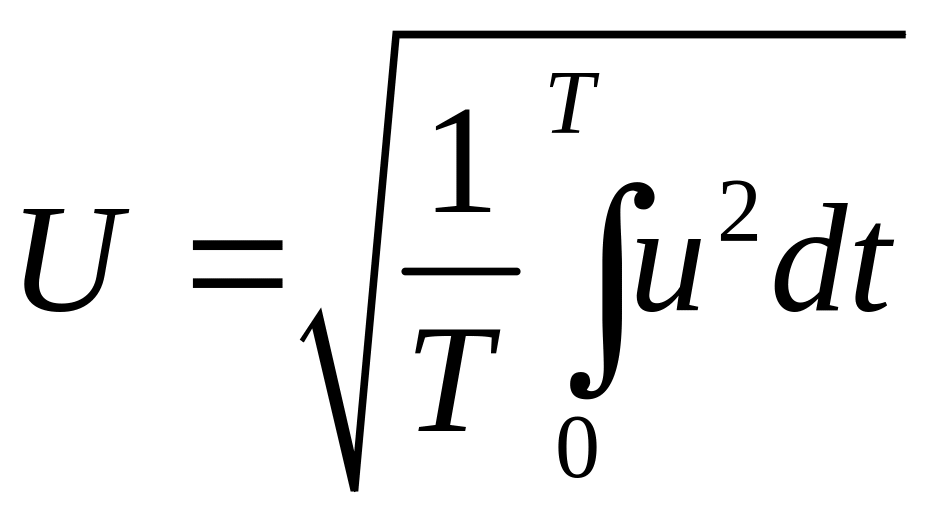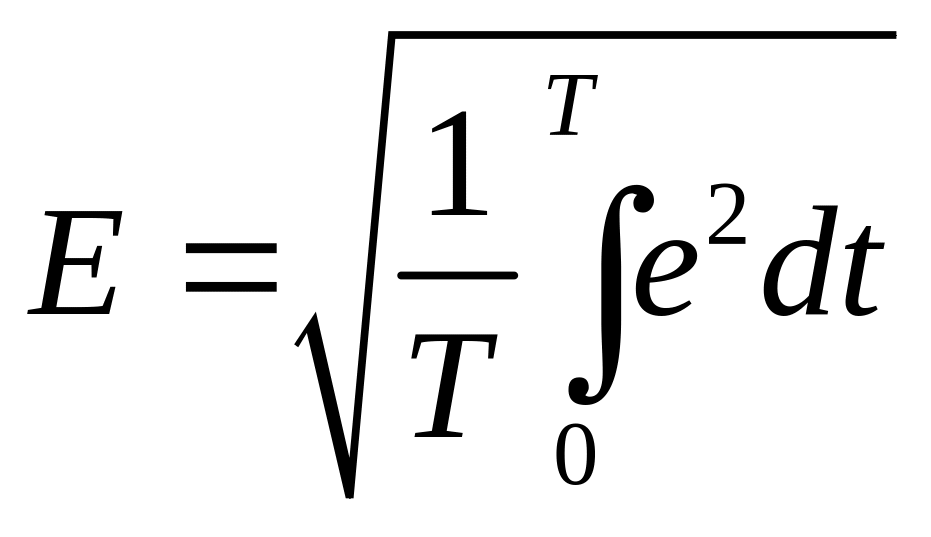, , . (1.2)

Например, действующее значение периодического тока равно такому значению постоянного тока, который, проходя через сопротивление r, за период Т выделяет то же количество тепла, что и данный переменный ток i.

Связь между амплитудным и действующим значениями синусоидального тока равна

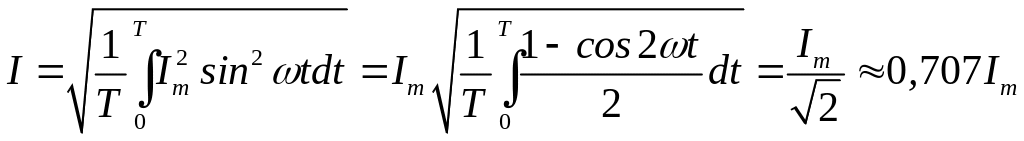.( ) (1.3)

Иногда гармонические сигналы характеризуют средним значением. Среднее значение синусоидальной величины за период равно нулю, поэтому за среднее значением гармонического тока принимают среднее значение за положительный полупериод:

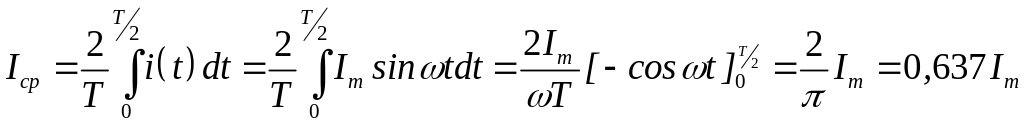. (1.4)

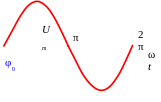
Разность фаз колебаний. При совместном рассмотрении двух гармонических сигналов (рис.1.2) одной частоты разность их начальных фаз, называют сдвигом фаз и обозначают

, где . (1.5)

Если φ=0,то напряжение и ток совпадают по фазе, если - находятся в противофазе, если - в квадратуре. Если φ>0, то отстает от по фазе на угол , если , то опережает по фазе на угол .

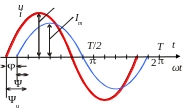
В электронике часто используются импульсы прямоугольной формы рис. 1.3. Они характеризуется следующими основными параметрами: u_m, –амплитуда, В; Т– период, cек; и τ – длительность импульса, cек.

Кроме них используют следующие параметры: 1. скважность - θ=Т/τ; 2. коэффициент заполнения - (τ/Т)100%; 3. постоянная составляющая (среднее значение за период) сигнала (напряжения) - .

Рис. 1.3. Периодическая последовательность прямоугольных импульсов

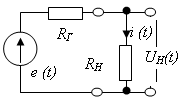
1.2. Основные параметры электрических цепей

Большинство электрических цепей служит средством передачи сигналов от источника сигнала в нагрузку (рис. ). При этом сигнал на входе цепи х(t) называют – воздействием или входным сигналом, а сигнал на выходе у(t) (на нагрузке)– откликом, реакцией или выходным сигналом.

Параметром цепи Н называют отношение величины выходного сигнала У, к величине входного сигнала Х,

Н=У/Х. (1.7)

В зависимости от вида входного сигнала различают три параметра цепи:

1. Статический параметр Н_ст =У₀/Х_0, где Х₀ и У₀ - постоянные величины;

2. Дифференциальный параметр H₀ есть отношение приращения отклика ΔY к приращению воздействия ΔX в заданной рабочей точке X₀ - Н₀=(ΔY/ ΔX) при X= X_0.

3. Комплексный параметр. Если входной сигнал гармонический с комплексной амплитудой Х_m=Х_mе^jφх, а цепь линейная, то выходной сигнал всегда гармонический с комплексной амплитудой У_m=У_mе^jφу. При этом параметр цепи становится комплексным числом - Н=У/Х = Hе^jφ - комплексный параметр цепи, где H=Y_m/X_m – модуль, а φ = φ₂- φ₁ - аргумент комплексного параметра.

Для двухполюсника основным параметром является сопротивление Z=U_m/I_m, причем воздействием считают ток I, а откликом напряжение U. Иногда пользуются проводимостью двухполюсника – Y= I_m /U_m.

Для четырехполюсника основным параметром считают коэффициент передачи по напряжению К_u=U_2m/U_1m, где U_2m и U_1m – комплексные амплитуды выходного и входного напряжений. Здесь К=Ке^jφк, где К=U_2m/U_1m и φк – модуль и аргумент коэффициента передачи.

Рис.1.4. Схема замещения источника сигнала с нагрузкой.

В простейшей электрической цепи, состоящей из генератора и нагрузки (рис.1.4), протекает гармонический ток:

i(t)= e(t)/(R_Г+R_Н)=(E_m/(R_Г+R_Н)) cos(t+)

Напряжение на нагрузке:

При R_Н>>R_Г амплитуда напряжения на нагрузке достигает максимальной величины, стремясь к амплитуде E_m–это режим согласования по напряжению.

Активная мощность, выделяемая в нагрузке, определяется соотношением:

Мощность P_Н достигает максимального значения P_{н max} когда R_Н = R_Г .Это режим согласования по мощности,.