Уравнение мещерского

(основное уравнение динамики тела переменной массы)

В современной технике возникают случаи, когда масса точки и системы не остается постоянной в процессе движения, а изменяется. Так, например, при полете космических ракет, вследствие выбрасывания продуктов сгорания и отдельных ненужных частей ракет, изменение массы достигает 90-95% общей начальной величины. Но не только космическая техника может быть примером динамики движения переменной массы. В текстильной промышленности происходит значительное изменения массы различных веретен, шпуль, рулонов при современных скоростях работы станков и машин.

Рассмотрим главные особенности, связанные с изменением массы, на примере поступательного движения тела переменной массы. К телу переменной массы нельзя непосредственно применить основной закон динамики. Поэтому получим дифференциальные уравнения движения точки переменной массы, применяя теорему об изменении количества движения системы.

Пусть точка массой m+dm движется со скоростью . Затем происходит отрыв от точки некоторой частицы массой dm движущейся со скоростью .

Количество движения тела до отрыва частицы:

Количество движения системы, состоящей из тела и оторвавшейся частицы, после ее отрыва :

Тогда изменение количества движения:

Исходя из теоремы об изменении количества движения системы:

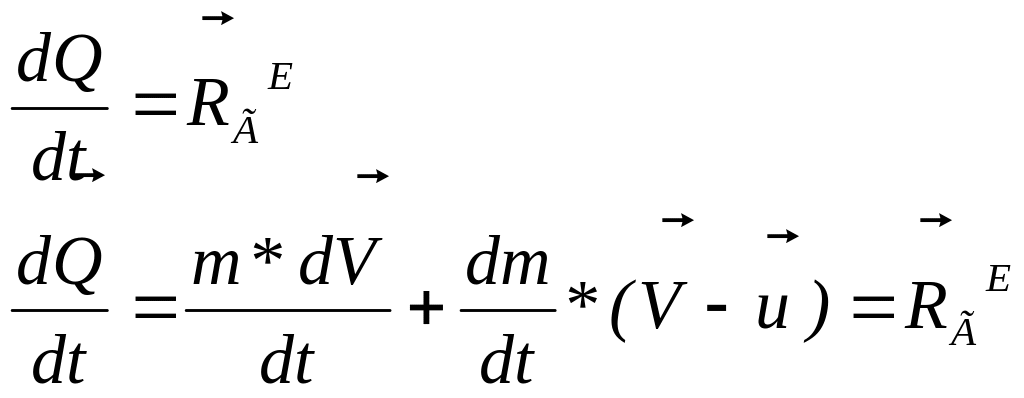
Обозначим величину - относительная скорость частицы:

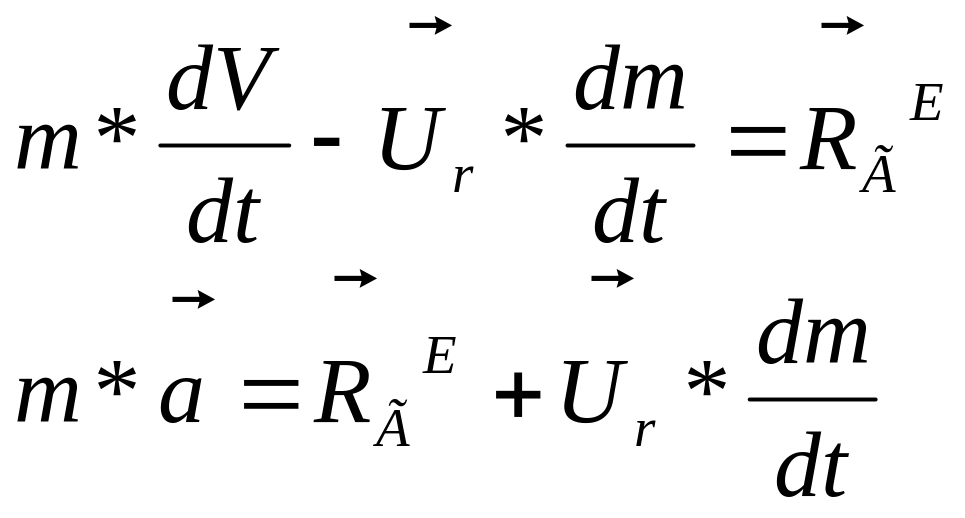
Обозначим

Величину R называют реактивной силой. Реактивная сила является тягой двигателя, обусловленная выбросом газа из сопла.

Окончательно получим

-

Данная формула выражает основное уравнение динамики тела переменной массы (формула Мещерского). Из последней формулы следует, что дифференциальные уравнения движения точки переменной массы имеют такой же вид, как и для точки постоянной массы, кроме приложенных к точке дополнительно реактивной силы, обусловленной изменением массы.

Основное уравнение динамики тела переменной массы свидетельствует о том, что ускорение этого тела формируется не только за счет внешних сил, но и за счет реактивной силы.

Реактивная сила – это сила, родственная той, которую ощущает стреляющий человек - при стрельбе из пистолета она ощущается кистью руки; при стрельбе из винтовки воспринимается плечом.

Первая формула Циолковского (для одноступенчатой ракеты)

Пусть точка переменной массы или ракета движется прямолинейно под действием только одной реактивной силы. Так как для многих современных реактивных двигателей , где - максимально допускаемая конструкцией двигателя реактивная сила (тяга двигателя); - сила тяжести, действующая на двигатель, находящийся на земной поверхности. Т.е. изложенное позволяет составляющей в уравнении Мещерского пренебречь и к дальнейшему анализу принять это уравнение в форме: ,

Обозначим:

- запас топлива (при жидкостных реактивных двигателях - сухая масса ракеты (остающаяся её масса после выгорания всего топлива);

- масса отделившихся от ракеты частиц; рассматривается как переменная величина, изменяющаяся от до .

Запишем уравнение прямолинейного движения точки переменной массы в следующем виде вид

.

Так как формула для определения переменной массы ракеты

Следовательно, уравнения движения точки Беря интегралы от обеих частей получим

,

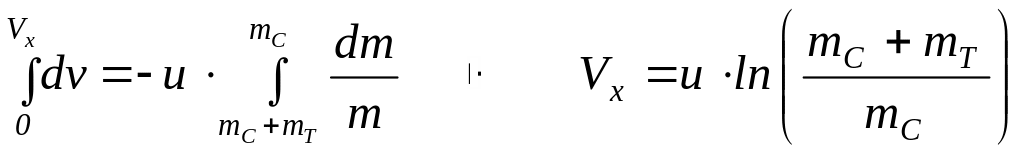где - характеристическая скорость – это скорость, которую приобретает ракета под действием тяги после извержения из ракеты всех частиц (при жидкостных реактивных двигателях – после выгорания всего топлива).

Вынесенная за знак интеграла (что можно делать на основании известной из высшей математики теоремы о среднем) - это средняя скорость извергаемых из ракеты частиц.

Вышеприведенное математическое выражение называют первой формулой Циолковского (или: формулой Циолковского для одноступенчатой ракеты), где - число Циолковского.

Как видим, с точки зрения получения наибольшего значения характеристической скорости, должна быть как можно большей величиной. Поэтому на практике - это максимально достижимая скорость извержения частиц из ракеты. К сведению: в наиболее распространённых жидкостных реактивных двигателях (окислитель - жидкий кислород, азотная кислота, перекись водорода и др.; горючее - керосин, спирт, жидкий водород и т.д.) может достигать значений 3-3,5 км/с иногда до 4,5 км/с. Реально достижимая характеристическая скорость - км/с. Чтобы ракета смогла возвратиться на Землю и не стала как Луна спутником Земли, при среднем расстоянием от земной поверхности в 200 км необходимо достигать скоростей не менее 7,9 км/с, т.е. характеристическая скорость должна быть не меньшей км/с.

Следовательно, одноступенчатая ракета не способна, по сегодняшнему уровню научно-технических достижений, преодолеть земное притяжение – неотвратимо будет возвращаться на земную поверхность. Но выход из положения есть- это многоступенчатые ракеты.