Вынужденные колебания

Пусть на материальную точку действуют восстанавливающая сила и возмущающая сила . При этом величина k будет являться угловой частотой собственных колебаний, а величина p – угловой частотой вынужденных колебаний. Силу сопротивления мы не учитываем.

Дифференциальное уравнение вынужденных колебаний:

;

,

где - приведенная амплитуда возмущающей силы.

Уравнение движения в зависимости от соотношения величин k и p имеет различный вид. В случае, когда ,

,

где ,

- постоянные интегрирования.

Амплитуда чисто вынужденных колебаний:

.

С другой стороны, воспользовавшись уравнениями , получим :

.

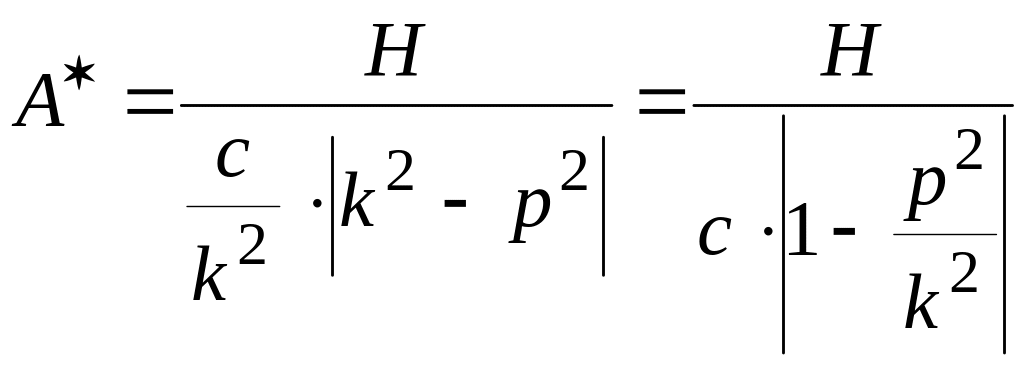Величина называется коэффициентом динамичности. Данный коэффициент показывает, во сколько раз амплитуда колебаний превосходит статическое отклонение при действии максимальной возмущающей силы H.

Рассмотрим случай, когда . Уравнение движения при этом будет такое же как и в предыдущем случае. График колебаний представлен на рис.3.13.

Рис.3.13

Такое движение называется биением.

Случай, когда . Уравнение движения:

.

График колебаний представлен на рис.3.14.

Рис.3.14

При таком движении происходит неограниченный рост амплитуды со временем. Это явление носит название резонанса. При резонансе коэффициент динамичности стремится к ∞ .

Решение задач

Условие задачи. Стержень OA длины l, на конце которого помещен груз массы m, может поворачиваться относительно оси O (рис. 3.15). На расстоянии a от оси O к стержню прикреплена пружина с коэффициентом жесткости c. определить круговую частоту колебаний груза, если стержень в положении равновесия занимает горизонтальное положение. Массой стержня пренебречь.

Рис.3.14

Решение. Круговую частоту колебаний груза определим по формуле

. (3)

Для этого сначала найдем эквивалентную жесткость эквивалентной пружины.

Рассмотрим равновесие груза A, укрепленного на стержне. Уравнение моментов относительно точки O сил, действующих на груз, будет иметь следующий вид:

,

где - сила упругости пружины в положении равновесия груза. Откуда

. (4)

Рассмотри теперь равновесие груза A на эквивалентной пружине. Уравнение равновесия груза имеет следующий вид:

,

где - сила упругости эквивалентной пружины в положении равновесия груза. С учетом этого получим

(5)

Приравнивая правые части выражений (4) и (5), получим

. (6)

Отношение найдем как отношение сторон a и l соответственно треугольника OAB:

. С учетом этого выражение (6) примет вид

.Найденное значение подставим в формулу (1):

.

ПРИМЕР 2. Найти период свободных вертикальных колебаний корабля на спокойной воде, если масса корабля М т, площадь его горизонтальной проекции S м^2. Плотность воды ρ= 1 т/м³. Силами, обусловленными вязкостью воды, пренебречь.

РЕШЕНИЕ. В процессе вертикальных колебаний на корабль действуют две силы: сила тяжести M g и выталкивающая корабль из воды сила Архимеда F_A. Условно, изобразим корабль в двух положениях (рис. 3.15); положении статического равновесия 1 и в произвольном положении 2 определяемом координатой x.

Рис. 3.15

Составим дифференциальное уравнение движения центра тяжести корабля:

Получено уравнение вида ,

где

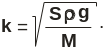
Следовательно,