Влияние постоянной силы на характер колебательного процесса

Рассмотрим материальную точку, подвешенную к пружине (рис.3.10). Начало отсчета O, как и раньше, выбираем в положении равновесия точки. Введем в рассмотрение величину - статическая деформация пружины под действием силы тяжести. При этом по модулю сила упругости .

Рассмотрим равновесие точки, когда она не совершает колебаний:

; . (2)

Рис.3.10

Теперь рассмотрим динамику колебаний:

; ,

где - проекция на ось Ox силы упругости пружины с учетом ее статической деформации;

;

.

С учетом выражения (2) получим

,

Последнее уравнение совпадает с ранее полученным дифференциальным уравнением свободных колебаний материальной точки, следовательно, постоянная по величине сила не оказывает влияния на колебательный процесс.

Свободные колебания математического маятника

Математическим маятником называется материальная точка, подвешенная на длинной нерастяжимой нити, массой которой можно пренебречь (рис.3.11). Обозначим l длину нити. Положение материальной точки будем определять криволинейной координатой s (углом φ) в естественных осях координат.

Рис.3.11

На тело действуют: сила натяжения нити и сила тяжести. Основное уравнение динамики спроецируем на тангенциальную ось:

; ;

; ;

; ;

; .

При малых углах φ отклонения от положения равновесия будет справедливо: .

Тогда

: ;

Получим дифференциальное уравнение, отражающее процесс колебаний математического маятника

,

где ; .

Колебания материальной точки при наличии вязкого трения

В реальных условиях колеблющаяся материальная точка всегда испытывает сопротивление движению. Рассмотрим прямолинейное движение материальной точки под действием восстанавливающей силы и силы вязкого сопротивления.

Дифференциальное уравнение колебаний при действии восстанавливающей силы и силы сопротивления имеет следующий вид:

;

Введем коэффициент

получим дифференциальные уравнения свободных колебаний при наличии вязкого сопротивлении

,

Коэффициент k – круговая частота – характеризует восстанавливающую силу, а коэффициент h характеризует силу сопротивления. Эти коэффициенты сопоставимы и имеют размерность 1/с.

Колебательный процесс существенно зависит от соотношения величин h и k.

Рассмотрим несколько случаев.

1. Случай малого сопротивления (h<k). Общее решение дифференциального уравнения :

,

где .

Колебания, происходящие по данному закону, называют затухающими, так как амплитуда с течением времени непрерывно уменьшается.

График, характеризующий данные колебания представлен на рис.3.12.

Рис.3.12

Влияние силы сопротивления выражается в том, что амплитуда колебаний уменьшается в геометрической прогрессии со знаменателем

,

где период затухающих колебаний

во все время движения остается постоянным. Величина η называется декрементом колебаний (фактором затуханий). Рассматривают также логарифмический декремент колебаний: .

В случае малых сопротивлений влиянием сопротивлений на величину периода колебаний можно пренебречь, полагая что

2. При случае, когда 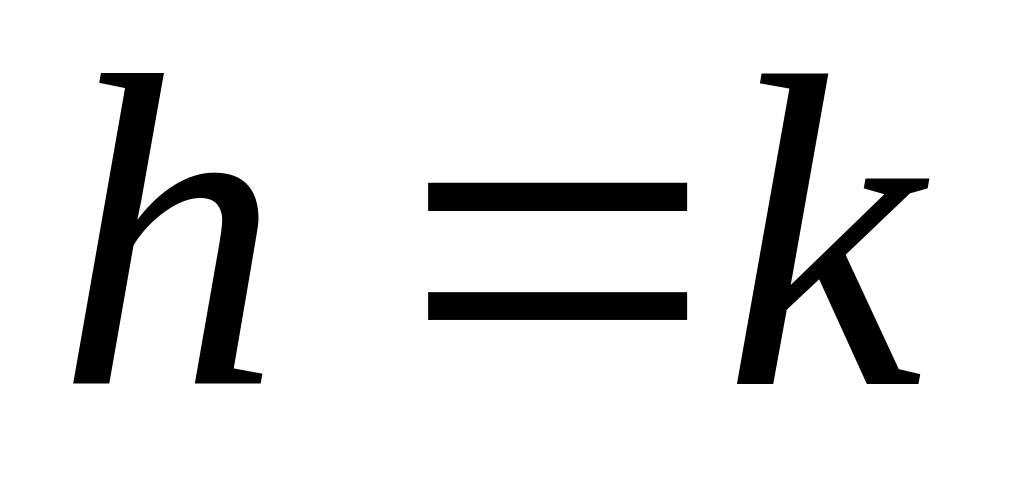(граничный случай)

Уравнения движения точки примут следующий вид

Из этой зависимости следует, что в рассматриваемом случае движение точки уже не носит колебательного характера, но остается затухающим движением, так как при .

Такое движение называется апериодическим. В данном случае точка, получив начальную скорость, достигнет положения, соответствующего максимальному отклонению от положения равновесия. А далее будет приближаться к положению равновесия. Ниже показан график, отражающий данный случай.