Velocity of a Particle.

Learn the following words and word combinations by heart:

appreciate	оценивать
arc of a path as	дуга пути, дуга траектории так как..
be called be equal to = equal	называться равняться …., быть равным
be tangent to a path	быть касательной к траектории пути
characterize speed	характеризовать скорость
chord	хорда
determination	определение
derivative of finally	производная в конце концов, в конечном счете
numerical value of obviously	цифровое значение … явно, очевидно
precisely rapidity ratio	точно, определенно, именно скорость соотношение, коэффициент
readily	легко, просто, без труда
scalar function secant	скалярная функция секущая, секанс
sign of … is the same as that of take into account	знак …такой же самый, как знак принимать во внимание
tangent	касательная; тангенс, касательная линия
tend to	стремиться к …
towards	по направлению к…, к

Ex.1. Look at Appendix 1 and read the following mathematical symbols and abbreviations.

cos a, S , t = t₁-t , V < 0 , V > 0, , , / t, d /dt, V= Vav = (S1-S)/(t1-t)= S/ t

Part 1 . Determination of the Velocity of a Particle when its Motion is described by the Vector Method.

Velocity of a Particle is the vector quantity characterizing speed (quickness, rapidity) and direction of change of a particle position.

Let a moving particle occupy at time t a position M defined by the radius vector and at time t₁ a position M1 defined by the radius vector (fig. 3).

We shall call the vector the displacement vector of the particle. This vector is directed along a chord. Then the average velocity of the particle M during the given time interval t=t1-t is called vector quantity

Vector has the same direction as vector , i.e. along the chord MM1 in the direction of the particle motion.

Obviously, the smaller the time interval t=t1-t for which the average velocity has been calculated, the more precisely will characterize the particle’s motion. To obtain a characteristic of motion independent on the choice of the time interval t, the concept of instantaneous velocity of a particle is introduced.

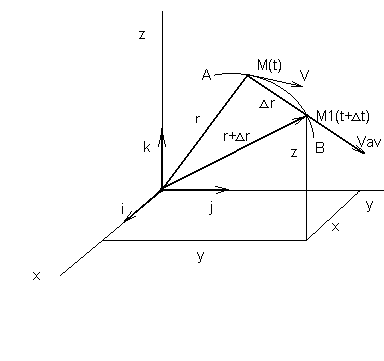
Fig.3

The instantaneous velocity of a particle at any time t is defined as the vector quantity towards which the average velocity tends when the time interval t tends to zero:

The limit of the ratio / t as t tends to zero is the first derivative of the vector with respect to t and is denoted, like the derivative of a scalar function, by the symbol d /dt.

Finally, we obtain = d /dt.

Thus, the vector of instantaneous velocity of a particle is equal to the first derivative of the radius vector of the particle with respect to time.

As the limiting direction of the secant MM₁ is a tangent, the vector of instantaneous velocity of a particle is tangent to the path of the particle in the direction of motion.

Comprehension check.

Ex 2. Answer the following questions.

1. What is the displacement vector directed along?

2. What is the velocity of a particle?

3. What is called the vector quantity?

4. Why is it necessary to introduce the concept of the instantaneous velocity of a particle?

5. What is the instantaneous velocity of a particle?

6. What is the vector of the instantaneous velocity of a particle equal to?