Part 1. Work and kinetic energy.

We can apply Newton's second law F = ma to various problems of particle motion to establish the instantaneous relationship between the net force acting on a par­ticle and the resulting acceleration of the particle. When intervals of motion were involved where the change in velocity or the corres­ponding displacement of the particle was required, we integrated the computed acceleration over the interval by using the appropri­ate kinematical equations.

There are two general classes of problems in which the cumulative effects of unbalanced forces acting on a particle over an in­terval of motion are of interest to us. These cases involve, respec­tively, integration of the forces with respect to the displacement of the particle and integration of the forces with respect to the time they are applied. We may incorporate the results of these integra­tions directly into the governing equations of motion so that it be­comes unnecessary to solve directly for the acceleration. Integration with respect to displacement leads to the equations of work and energy, which are the subject of this article.

Part 2. Work

The quantitative meaning of the term work will now be developed. Figure 3/2a shows a force F acting on a particle at A which moves along the path shown. The position vector r meas­ured from some convenient origin 0 locates the particle as it passes point A, and dr is the differential displacement associated with an infinitesimal movement from A to A'. The work done by the force F during the displacement dr is defined as

dU = F• dr

The magnitude of this dot product is dU = F ds cos a, where a is the angle between F and dr and where ds is the magnitude of dr. This expression may be interpreted as the displacement multiplied by the force component F_t = F cos a in the direction of the displacement as represented by the dotted lines in Fig. 3/2 b. Alternatively, the work dU may be interpreted as the force multiplied by the displacement component ds cos a in the direction of the force, as represented by the full lines in Fig. 3/2 b.

With this definition of work, it should be noted that the component F_n = F sin a normal to the displacement does no work. Hence, the work dU may be written as

dU = F_t ds.

Work is positive if the working component F_t is in the direction of the displacement and negative if it is in the opposite direction. Forces that do work are termed active forces. Constraint forces that do no work are termed reactive forces.

In SI units work has the units of force (N) times displacement (m) or N • m. This unit is given the special name joule (J), which is defined as the work done by a force of 1N moving through a distance of 1 m in the direction of the force. Consistent use of the joule for work (and energy), rather than the units N•m will avoid possible ambiguity with the units of moment of a force or torque, which are also written N • m.

It should be noted that work is a scalar as given by the dot product and involves the product of a force and a distance, both measured along the same line. Moment, on the other hand, is a vector as given by the cross product and involves the product of force and distance measured at right angles to the force.

During a finite movement of the point of application of a force, the force does an amount of work equal to

U = F• dr =  (F_X dx + F_y dy + F_z dz) or

U =  F_t ds

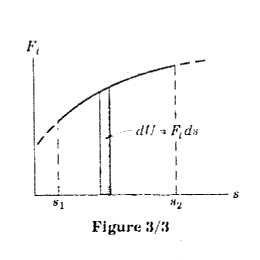
In order to carry out this integration, it is necessary to know the relations between the force components and their respective coor­dinates or the relation between F_t and s. If the functional relation­ship is not known as a mathematical expression which can be integrated but is specified in the form of approximate or experimental data, then the work may be evaluated by carrying out a numerical or graphical integration which would be represented by the area under the curve of F_t versus s as shown in Fig. 3/3.

Comprehension check. (Parts 1 and 2.)

Ex. 1. Answer the following questions.

1. What can be established applying Newton's second law F = ma to various problems of particle motion ?

2. When are cumulative effects of unbalanced forces acting on a particle over an in­terval of motion of interest to us?

3. When is work positive? and negative?

4. What forces doing work are termed active forces? and reactive forces?

5. Why is work a scalar ?

6. Why is moment a vector?

Ex.2. Complete the following sentences with the information from the text.

1. Integration with respect to displacement leads to…..

2. The position vector r meas­ured from some convenient origin 0….

3. In SI units work has the units…..

4. Moment, on the other hand, is a vector……

5. In order to carry out this integration…….

Ex. 3. Insert the most suitable word into the gaps.

We can apply Newton's second ……..F = ma to various problems of particle …….to establish the instantaneous relationship …….. the net force acting on a par­ticle and the resulting acceleration of the ……... When intervals of …….. are involved where the change …….velocity or the corres­ponding displacement of the particle ……. required, we can integrate the computed acceleration over the interval by using the ……..kinematical ……….

There are …….. general classes of problems in which the cumulative effects of unbalanced forces …….. on a particle over an ……..of motion are of interest to us. These cases involve, respec­tively, integration of the forces with ……. to the displacement of the particle and ……of the forces with respect to the time they are …….

Ex.4. Transform the following sentences from Passive into Active.

1. The quantitative meaning of the term work will now be developed.

2. The work done by the force F during the displacement dr is defined as dU = F• dr.

3. This expression may be interpreted as the displacement multiplied by the force component.

4. If the functional relation­ship is not known as a mathematical expression then the work may be evaluated by carrying out integration.

5. The functional relation­ship is specified in the form of approximate or experimental data.

6. Integration would be represented by the area under the curve of F_t versus s as shown in Fig. 3/3.