Verbs: obtain, perform, belong, lie, erect, exist , lead.

Prepositions: to, in, from, by, at, for.

1. This point ………..the section S of the body.

2. If a body is in non-translational motion, only one instantaneous centre of zero velocity always ………any instant t.

3. We can ……..the same result …….any other point of the body.

4. The velocity of any point of a body which ……section S is equal to the velocity of its rotation about the instantaneous centre of zero velocity P.

5. The results of this investigation ……..the following conclusion.

6. It is necessary to ……..perpendiculars ……..points A and B to their respective velocities.

7. The plane motion is ……… a cylinder rolling without slipping along a fixed cylindrical surface.

Ex. 8. Match the adjectives in the left column with the nouns in the right one, adjectives and nouns can be used more than once.

Adjectives		Nouns
1	angular	a	answer
2	contacting	b	velocity
3	given	c	result
4	parallel	d	instant
5	previous	e	method
6	respective	f	quantity
7	same	g	case
8	simple
9	special
10	visual

Unit 12.

Motion of a Rigid Body Having One Fixed Point.

Learn the following words and word combinations by heart:

accordingly	соответственно
angle of nutation	угол наклона
arrow	стрелка
attach rigidly	закреплять (подсоединять) жёстко (без шарниров) , неподвижно
ball-and-socket joint	шарнирное соединение; шаровое соединение
be compounded of	состоять из…, быть составленным из
by the same reasoning coincide with conclude continuously	по тем же соображениям совпадать с … прийти к заключению, сделать вывод, заключать постоянно, все время
describe a curve in space	описывать кривую в пространстве
displacement elementary ~ oppositely directed ~ resultant ~ Euler angle	перемещение элементарное, бесконечно  малое перемещение (точки) противоположно направленное перемещение результирующее перемещение,  смещение эйлеров угол
impart	сообщать движение, ускорение; передавать энергию
intersect	пересекать; перекрещивать; проходить через (что-л.);
hodograph of a vector	годограф вектора
kinematics characteristics	кинематические характеристики
lie outside line of nodes nutation precession proper rotation	находиться лежать за пределами линия узловых точек; оптическая ось нутация прецессия, прецессионное движение собственное вращение
respective point	соответствующая (соответственная ) точка
same	один и тот же, одинаковый
series of consecutive elementary rotations about axis	Ряд последовательных элементарных вращений вокруг оси
simultaneously	одновременно
spin	вращаться (вокруг своей оси)
time ra­te of change	производная по времени; скорость  изменения со временем, ускорение  при  разгоне  или  замедлении (рабочего органа)
trihedron	триэдр; тройка ортов
unlike (the case)	в отличие от (случая)
yield	образовывать

Ex.1. Look at Appendices 1 and 2 and read the following mathematical symbols and Greek letters.

KOx, = < x1OK, = < z1Oz,

Let us investigate the motion of a body having a fixed point 0 with respect to a reference system ox1y1. Any body with a ball-and-socket joint is the illustration of such motion. Let us find the parameters that determine the position of a body having one fixed point. For this, assume the body is rigidly attached to the trihedron Oxyz whose position defines the position of the body (Fig. 25).

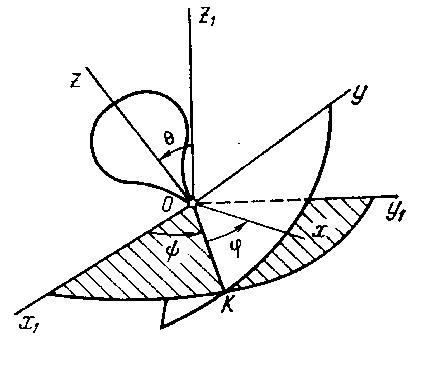
Fig. 25

Line OK, along which planes Oxy and Ox1y1 intersect, is called the line of nodes. The position of the trihedron Oxyz, and hence of the body, with respect to the axes Ox1y1 is given by the angles: KOx, = < x1OK, = < z1Oz.

These angles, called the Euler angles, are known by the following names, taken from celestial mechanics: —the angle of proper rotation, —angle of precession, — angle of nutation. The positive directions are shown in Fig. 25 by arrows. A change in angle  indicates a rotation of the body around axis Oz (proper rotation), a change in angle  indicates a rotation around axis 0z1 (precession), and a change in angle indicates a rotation around the line of nodes OK (nutation).

To describe the body's motion, its position with respect to axes Ox1y1z1 must be known for any instant, i.e.,

Equations (65) define the law of motion and are called the equa­tions of motion of a rigid body about a fixed point.

To get a full picture of this type of motion, let us demonstrate the following theorem of Euler-d’Alembert: Any elementary displacement of a body having a fixed point represents an elementary rotation about an instantaneous axis of rotation through that point .

Let the body’s position be given by the angles . Then its displacement in an elementary time interval dt can be represented as the resultant of a series of rotations through angles d,d and d about axes Oz, Oz₁ ,and OK, respectively. Combined, the three rotations yield the true elementary displacement of the body.

Consider first the resultant displacement of the rotations about axes Oz and Oz₁ (Fig. 26). A rotation through angle d, about axis Oz imparts to any point of the body in the plane zOz₁ (inside angle z0z₁) an elemen­tary displacement perpendicular to the plane and equal in magnitude to h1d, where h1 is the distance of the point from axis Oz. Simultaneously, in the ro­tation about axis Oz1 , the point will receive an oppositely directed displace­ment of magnitude h2d. Accordingly, within angle zOz₁ , there will always be a point B for which

h1d = h2d and whose displacement is zero (if the direc­tion of rotation is opposite to that shown in Fig. 26, the point lies outside angle zOz₁). Hence we conclude that the body's elementary displacement resulting from the rotations about axes Oz and Oz1 is the same as the displacement of a body with two stationary points 0 and B, i.e., it is an elementary rotation about axis OB through point 0.

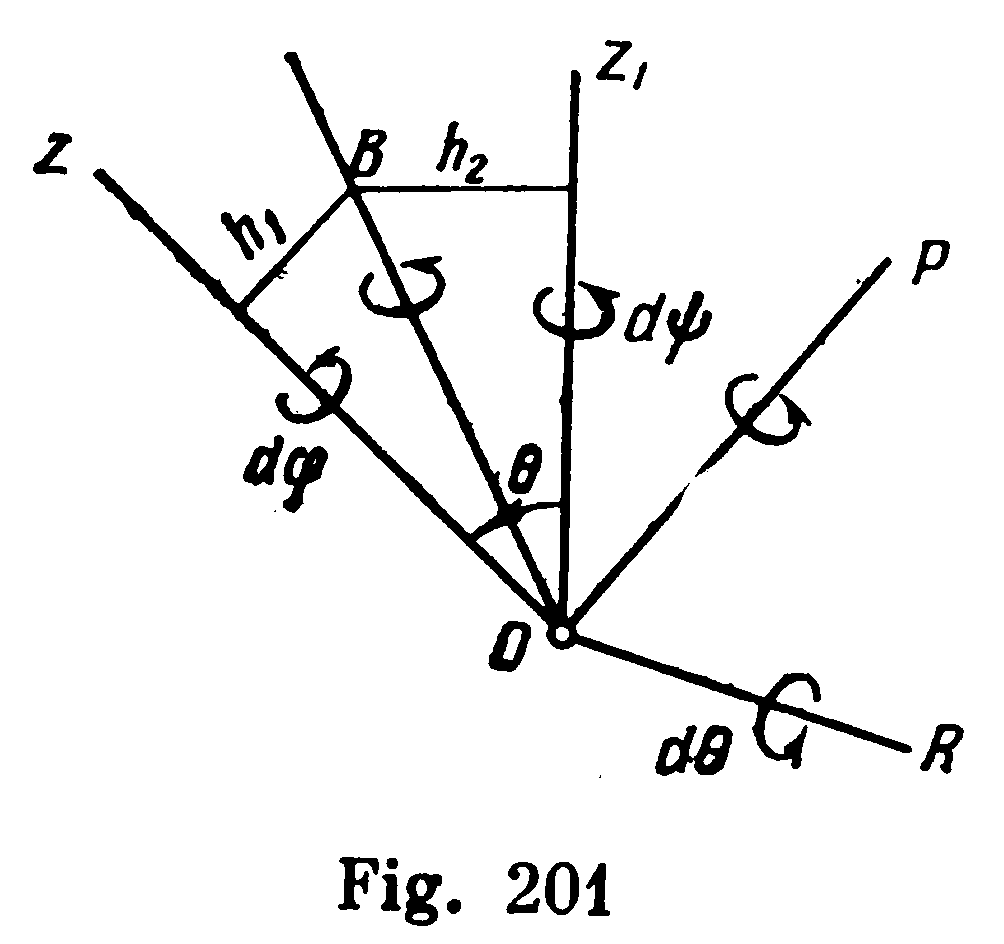
Fig. 26

By the same reasoning, the elementary rotations about axes OB and OK are equivalent to an elementary rotation about an axis OP through point 0 (Fig. 26), and the theorem is proved.

Axis OP is called the instantaneous axis of rotation ; an elementary rotation of the body about it brings the body into a neighbouring position infinitesimally close to the given position; the velocities of all points of the body lying on the instantaneous axis of rotation are zero. Unlike a fixed axis, the instantaneous axis of rotation con­tinuously changes its direction in space and in the body. The rota­tion about axis OP, which brought the body into the neighbouring position, is followed by a rotation about the new instantaneous axis of rotation OP1 , etc. Thus, the motion of a rigid body about a fixed point is compounded of a series of consecutive elementary rotations about instantaneous axes of rotation through that fixed point (Fig. 26).

Let us examine the kinematics characteristics of this motion.

(1) The angular velocity  with which a body makes an elementa­ry rotation about the instantaneous axis of rotation is called the instantaneous angular velocity of the body. It can be denoted by a vector  directed along axis OP. As the direction of axis OP changes continuously, vector  changes with time both in magnitude and direction, and its tip A describes a curve AD in space, which is the hodograph of vector (Fig. 27).

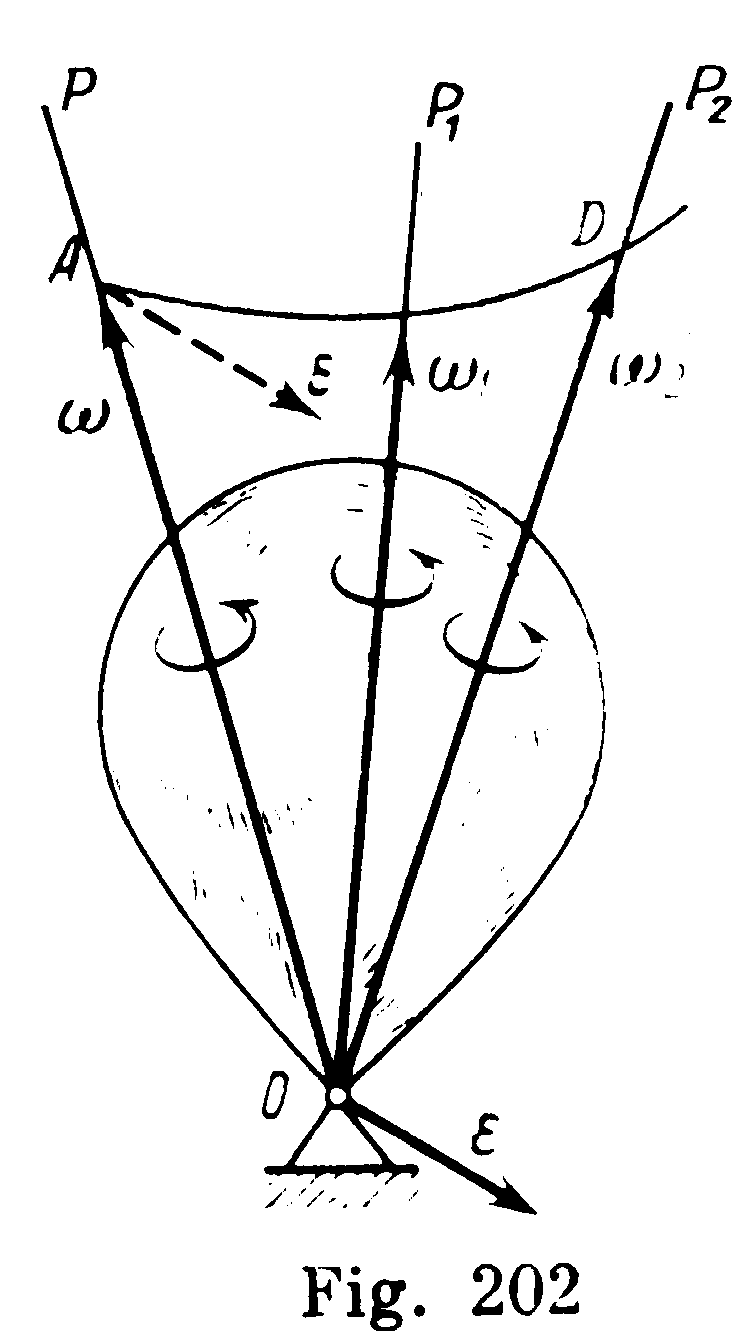
Fig. 27

(2) The instantaneous angular acceleration of a body, which characterizes the time ra­te of change of the angular velocity  both in magnitude and direction, is a vector qu­antity

Comparing this expression with the equa­tion v == dr/dt, we conclude that the angular acceleration  can be computed as the velocity with which the tip of vector  moves along curve AD (see Fig. 27). Specifi­cally, the direction of  coincides with the direction of the tangent to curve AD at the respective point. Consequently, unlike the case of rotation about a fixed axis, the direction of vector  does not coincide with that of vector .

Vectors  and  are the basic kinematic characteristics of the motion of a body having a fixed point. They can be computed when the equations of motion (65) are known.

Comprehension check.

Ex.2. Answer the following questions.

1. What line is called the line of nodes?

2. What do the changes in angle , angle  and angle  indicate respectively?

3. What is the formulation of the theorem of Euler-d’Alembert?

4. How can we represent the displacement of a body’s position in an elementary time interval ?

5. What does a rotation through angle d about axis Oz impart to the body?

6. What axis is called the instantaneous axis of rotation?

7. What are the velocities of all points of the body lying on the instantaneous axis of rotation ?

8. What is the motion of a rigid body about a fixed point compounded of?

Ex.3.Say whether the following statements are True or False.

1. The change in angle  indicates a rotation of the body around the line of nodes OK (nutation).

2. The displacement of a body in a time interval dt is a series of rotations through angles d,d and d about axes Oz, Oz1 ,and OK, respectively.

3. Both, the fixed and the instantaneous axes of rotation con­tinuously change their directions in space and in the body.

4. Vector  of the angular velocity is directed along axis OP.

5. The tip A of the angular velocity describes a straight line in space.

6. The direction of vector  of angular acceleration coincides with the direction of vector  of the angular velocity.

Ex.4. Complete the following sentences with the information from the text.

1. We assume the body is rigidly attached to……

2. The line of nodes is….

3. The displacement of a body in an elementary time interval dt can be represented…..

4. The body's elementary displacement resulting from the rotations about axes Oz and Oz_1….

5. An elementary rotation of the body about instantaneous axis of rotation brings the body……

6. The angular acceleration  can be computed…..

Ex. 5. Match the verbs in the left column with the nouns in the right one, verbs and nouns can be used more than once.

Verbs		Nouns
1	attach	a	the parameter
2	consider	b	a full picture
3	define	c	the body
4	determine	d	one fixed point
5	find	e	an elementary rotation
6	get	f	a rotation
7	have	g	by arrow
8	indicate	h	from celestial mechanics
9	represent	i	the direction
10	show	j	the position
11	take from	k	the resultant displacement
		l	law of motion

Ex.6. Fill in the following verbs in the appropriate form and a correspondent preposition.

Verbs: give, compare, bring, take, follow, coincide, impart

Prepositions: to , with, into, by, from.

1. The direction of vector  does not ………that of vector .

2. We can …….. this expression …..with the one evolved from the previous theorem.

3. The position of the trihedron Oxyz, and hence of the body, with respect to the axes Ox₁y_1, is _{…………….} the angles ,  and .

4. The names for the Euler angles are ………the celestial mechanics.

5. A rotation through angle d, about axis Oz ……any point of the body in the plane zOz₁ an elemen­tary displacement perpendicular to the plane.

6. An elementary rotation of the body about the instantaneous axis of rotation …….the body ……..a neighbouring position infinitesimally close to the given position.

7. The rota­tion about the instantaneous axis of rotation is ………..a rotation about the new instantaneous axis of rotation.

Ex.7. Use the correct form of the word in bracket.

1. By the same …………(reason) , the …………..(element) …………(rotate) about axes OB and OK are ………..equivalent to an …………..(element) …………(rotate) about an axis OP through point 0. Axis OP is called the ……………(instant) axis of …………(rotate) ; an …………..(element) …………(rotate) of the body about it brings the body into a …………(neighbour) position infinitesimally close to the ………(give) position; the velocities of all points of the body …………(lie) on the……………(instant) axis of …………(rotate) are zero. …….. (like) a fixed axis, the ………………………(instant) axis of…………(rotate) ……….(con­tinue) changes its ………(direct) in space and in the body.

2. …………(Specify) , the …………(direct) of  coincides with the ………… (direct) of the tangent to curve AD at the………..( respect) point. Consequently, …….. (like) the case of …………(rotate) about a ……..(fix) axis, the …………(direct) of vector  does not coincide with that of vector .

Ex. 8. Translate from Russian into English.

1. Необходимо найти параметры, определяющие положение тела, имеющего одну неподвижную точку.

2. Если тело вращается вокруг оси, то оно получает противоположно направленное смещение.

3. Мгновенная ось смещения постоянно изменяет свое направление в пространстве и в теле.

4. Мгновенное угловое ускорение тела является векторной величиной.

5. Мгновенное угловое ускорение характеризует скорость изменения по времени угловой скорости как по величине, так и по направлению.

6. Значение векторов  и  можно вычислить, если известно уравнение движения.

Unit 13.