Verbs : design, lead to, construct, consider, specify, move, determine, join, calculate, perform.
Knowing this parameter we can define the velocity of a body.
This problem solution usually results into the sophisticated computation.
The projections of the velocities of two points of a rigid body on the straight line connecting those points are equal.
Let’s investigate any two points belonging to this straight line.
We should build a parallelogram in order to find the magnitude and direction of the velocity .
Plane motion of a rigid body is a combination of translation in which all points of the body translate with the velocity of the pole and rotation about that pole.
This vector determines the position of point M with reference to the axes Ax'y'.
The axes Ax'y' do translational motion together with pole A.
Ex.6. Match the verbs and nouns . Some nouns can be used more than once.
-
Verbs
Nouns
1
investigate
a
from the equation
2
follow
b
a position of a mechanism,
3
perform
c
about pole A
4
analyze
d
the coordinates of the point
5
specify
e
the motion of individual points
6
rotate
f
a parameter
7
express
g
with the velocity
8
eliminate
h
translation motion
9
move
Ex.7. Complete the following table:
Noun |
Verb |
Adjective |
|
|
descriptive |
|
investigate |
|
|
|
quantitative |
acceleration |
|
|
equation |
|
|
|
construct |
|
computation |
|
|
|
|
straight |
Ex. 8. Translate the following word combinations into English. Compose 5 sentences with any of them.
Предлагать более простой и удобный метод; тоже самое тело; в этом уравнении; полюс А неподвижен; другими словами (иначе говоря); строго говоря; предыдущее уравнение; геометрическая сумма; величина скорости.
Unit 11.
Determination of the Velocity of a Point of a Body Using the Instantaneous Centre of Zero Velocity. Centrodes.
Learn the following words and word combinations by heart:
be performed by |
осуществляться; производиться |
centrode |
центроида (геометрическое место мгновенных центров вращения) |
erect perpendiculars from point A to…. |
восстанавливать (строить) перпендикуляры из точки А к….. |
extension (of a body) |
протяжение; расширение; увеличение (тела) |
immediately |
немедленно, сразу же, тот час |
instantaneous ~ centre of zero velocity |
мгновенный; моментальный мгновенный центр нулевой скорости |
~ distribution of the velocities |
мгновенное распределение скоростей |
~ translation
non-translational motion
in terms of |
мгновенное прямолинейное, поступательное перемещение непрямолинейное, непоступательное движение в переводе на; в форме; исходя из; на основании |
intersection |
пересечение; точка или линия пересечения (напр. двух плоскостей) |
involve |
влечь за собой; охватить; состоять из |
lead to |
приводить к …. |
lie in infinity |
лежать, находиться в бесконечности, безграничности |
roll slipping |
колебаться вокруг оси скольжение, проскальзывание (в муфте) |
sense of rotation of a body
specify a position slip |
направление вращения (направление обхода, сторона вращения ) тела определить положение буксовка; проскальзывание; буксование |
Validity
verify |
достоверность; истинность; проверка правильности выверить; доказать; подтвердить |
whence |
который, из какого места?; из какого источника? |
Ex.1. Look at Appendix 1 and read the following mathematical symbols .
,
,
,
,
Another
simple and visual method of determining the velocity of any point of
a body performing plane motion is based on the concept of
instantaneous centre of zero velocity. The
instantaneous centre of zero velocity is
a point belonging to the section S of a body or its extension, which
at the given instant is momentarily at rest. It will be readily
noticed that if a body is in non-translational motion, such one and
only one point always exists at any instant t. Let points A and B in
section S of a body (Fig. 22)
have, at time t, non-parallel velocities
and
.
Then point P of intersection of perpendiculars Aa to vector
and Bb to vector
will
be the instantaneous centre of zero velocity, as
.
For, if we assumed that
,
then, by the theorem of the projections of the velocities of the
points of a body, vector
would
have to be simultaneously perpendicular to AP (as
)
and to BP (as
),
which is impossible. It also follows from the theorem that, at the
given instant, no other point of section S can have zero velocity
(e.g., for point a, the projection of
on
Ba is not zero and consequently
).
Fig. 22
If, now, we take a point P as the pole at time t, the velocity of point A will, by Eq. (50), be
,
as . The same result can be obtained for any other point of the body. Thus, the velocity of any point of a body lying in section S is equal to the velocity of its rotation about the instantaneous centre of zero velocity P. From Eqs. (51) we have
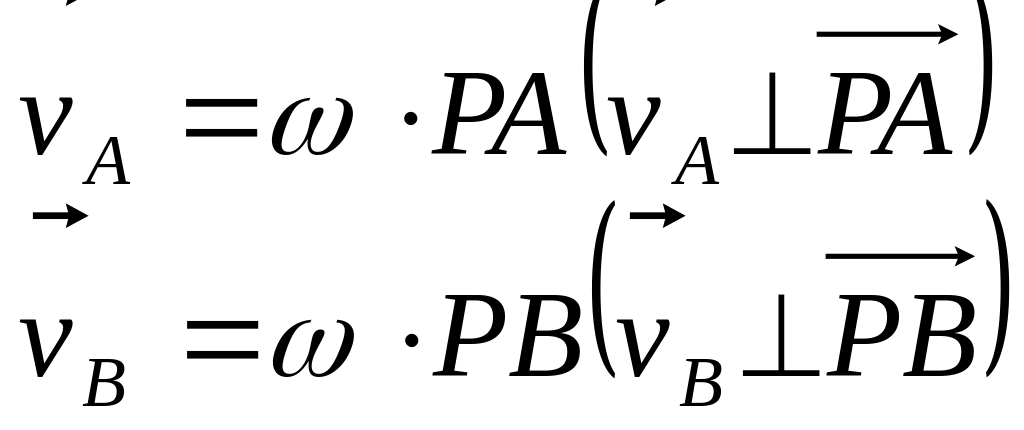, etc. (53)
It also follows from Eqs. (53) that
, (54)
i.e., that the velocity of any point of a body is proportional to its distance from the instantaneous centre of zero velocity.
These results lead to the following conclusions:
(1) To determine the instantaneous centre of zero velocity, it is sufficient to know the directions of the velocities and of any two points A and B of a section of a body (or their paths); the instantaneous centre of zero velocity lies at the intersection of the perpendiculars erected from points A and B to their respective velocities, or to the tangents to their paths.
(2)
To determine the velocity of any point of a body, it is necessary to
know the magnitude and direction of the velocity of any point A of
that body and the direction of the velocity of another point B of the
same body. Then, by erecting from points A and B perpendiculars to
and
,
we obtain the instantaneous centre of zero velocity P and, from the
direction of
,
the sense of rotation of the body. Next, knowing
,
we can find from Eq. (54) the velocity
of
any point M of the body. Vector
is perpendicular to
in the direction of the rotation.
(3) The angular velocity of a body, as can be seen from Eqs. (53), is at any given instant equal to the ratio of the velocity of any point belonging to the section S’ to its distance from the instantaneous centre of zero velocity P:
(55)
Let
us evolve another expression for ω.
It follows from Eqs. (50) and (51) that
and
whence
. (56)
When = 0 (point A is the instantaneous centre of zero velocity), Eq. (56) transforms into Eq. (55).
Fig. 23
Eqs. (55) and (56) give the same quantity, it follows that the rotation of the section S about either point A or point P takes place with the same angular velocity.
It is easy to verify that both equations give the same answer.
Let us consider some special cases of the instantaneous centre of zero velocity.
(a) If plane motion is performed by a cylinder rolling without slipping along a fixed cylindrical surface, the point of contact P (for the section shown in Fig. 23) is momentarily at rest and, consequently, is the instantaneous centre of zero velocity ( because if there is no slipping, the contacting points of both bodies must have the same velocity, and the second body is motionless). An example of such motion is that of a wheel running on a rail.
(b)
If the velocities of points A and B of the body are parallel to each
other, and AB is not perpendicular to
(Fig.
24
a)
the instantaneous centre of zero velocity lies in infinity, and the
velocities of all points are parallel to
.
From the theorem of the projections of velocities it follows that
,
i.e.,
;
the result is the same for all other points of the body.
Consequently, in this case the velocities of all points of the body
are equal in magnitude and direction at every instant, i.e., the
instantaneous distribution of the velocities of the body is that of
translation (this state of motion is also called instantaneous
translation). It will be found from Eq. (56) that the angular
velocity ω
of
the body at the given instant is zero.
Fig. 24
(c) If the velocities of points A and B are parallel and AB is perpendicular to , the instantaneous centre of zero velocity P can be located by the construction shown in Fig. 24 b. The validity of this construction follows from the proportion (54). In this case, unlike the previous ones, we have to know the magnitudes of velocities and to locate the instantaneous centre of zero velocity P.
(d)
If the velocity vector
of
a point in section S and the angular velocity ω
are known, the position of the instantaneous centre of zero velocity
P, lying on the perpendicular to
can
be immediately found from Eq. (55), which yields
.
Comprehension check.
Ex.2. Put the questions to the following answers.
It is the point belonging to section S of a body which is momentarily at rest at the given instant.
Only one.
To the velocity of its rotation about the instantaneous centre of zero velocity P.
It is proportional to the distance of a point from the instantaneous centre of zero velocity.
The directions of the velocities and of any two points A and B of a section of a body .
To the ratio of the velocity of any point belonging to the section S’ to its distance from the instantaneous centre of zero velocity P.
Ex.3.Say whether the following statements are True or False.
Angular velocity of a body depends on time, it changes with time.
The instantaneous centre of zero velocity is always at rest.
If the velocities of points A and B of the body are parallel to each other, and AB is not perpendicular to , the instantaneous centre of zero velocity lies in infinity.
Angular velocity of a body depends on the velocity of any point belonging to the section S’ and its distance from the instantaneous centre of zero velocity.
If plane motion is performed by a cylinder rolling without slipping along a fixed cylindrical surface, the instantaneous centre of zero velocity lies in infinity.
To determine the velocity of any point of a body, it is necessary to know only the magnitude and direction of the velocity of any point A of that body.
Ex.4. Find in Part B the antonyms for the words in Part A. There can be more than one antonym.
Part A. Special, visual method, point of the body, instant, at rest, fixed, unlike, same, intersection, impossible, previous, easy.
Part B. Different, common, complicated, possible, usual, like, audible method, parallelism, the whole body, eternity, subsequent, infinity, in motion, flexible, difficult, loose, real, similar.
Ex.5. Complete the following sentences with the information from the text.
To determine the instantaneous centre of zero velocity, it is sufficient …….
The instantaneous centre of zero velocity lies at the …..
By erecting from points A and B perpendiculars to and , we obtain ……
From the direction of we can obtain ……
If there is no slipping, the contacting points of both bodies ….
If the velocities of points A and B are parallel and AB is perpendicular to , the instantaneous centre of zero velocity P………
Ex.6. Match the terms and their definitions. Compose 5 sentences with any of them.
1 |
erect |
c |
to get smth that you want especially through your own effort, skill or work |
2 |
locate |
a |
to produce a result, answer or a piece of information |
3 |
obtain |
d |
to happen |
4 |
perform |
g |
to fix all the pieces of smth together and put it in an upright position |
5 |
slip |
h |
to state that smth is true, to find out if a fact is correct or true, to check |
6 |
take place |
f |
move quickly, smoothly, without any resistance |
7 |
verify |
e |
to find the exact position of smth |
8 |
yield |
b |
to work or do smth |
Ex.7. Fill in the following verbs in the appropriate form and the prepositions: