2) The verbs in the left column with the nouns in the right one.

The words in the right columns can be used more than once.

	Adjectives		Nouns			Verbs		Nouns
1	angular	a	body		1	consider	a	without motion
2	average	b	point		2	describe	b	towards the value
3	circular	c	angle		3	determine	c	in radians
4	fixed	d	velocity		4	measure	d	the position
5	positive	e	path		5	remain	e	path
6	principal	f	motion		6	specify	f	the angle
7	rigid	g	acceleration		7	tend
8	rotational	h	characteristics		8	turn through

Ex.8. Find in the text the adjectives corresponding to the following nouns :

Dimension, angle, motion, fix, rigidity, rotation, negation, correspondence, opposition, acceleration.

Ex.9. Translate the following phrases into English.

Так как расстояние между точками; очевидно, что при вращательном движении; в то время как все другие точки твердого тела; чтобы определить положение вращающегося тела; таким образом, угловая скорость тела; такой вектор одновременно указывает и на направление вращения; легко заметить, что; по аналогии с…..

Unit 8.

Velocities and Accelerations of the Points of a Rotating Body.

Learn the following words and word combinations by heart:

apply	применять, использовать
confuse (sm with sm or sb)	смешивать, спутывать
consider	рассматривать, считать, полагать
establish	устанавливать, определять, выяснять, создавать
in order to	для того, чтобы
inclination	наклон, уклон, угол наклона
investigate	исследовать, изучать, тщательно рассматривать
obtain	получать, доставать, достигать
reverse	n - обратное, противоположное чему-либо; противоположность adj - обратный, противоположный v -менять на противоположный
substitute ( for sm, sb)	заменять, подменять, замещать кого-либо, что-либо

Ex.1. Look at Appendices 1 and 2 and read the following mathematical symbols and Greek letters.

, ,

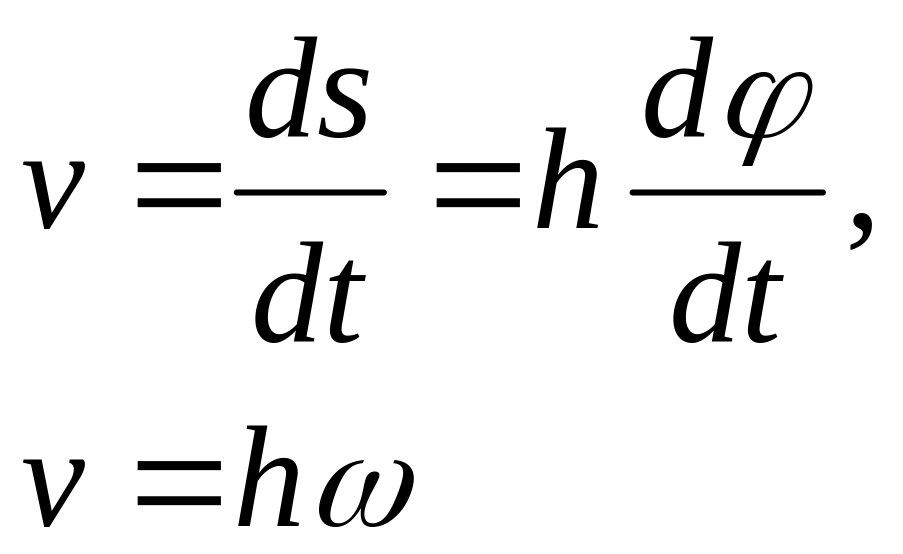
Having established the characteristics of the motion of bodies as a whole, let us now investigate the motion of the individual points of a body.

Consider a point M of a rigid body at a distance h from the axis of rotation Az (Fig. 11). When the body rotates, point M describes a circle of radius h in a plane perpendicular to the axis of rotation with its centre C on that axis. If in time dt the body makes an infinitesimal displacement through an angle d φ, point M will have made a very small displacement ds = h df along its path. The velocity of the point is the ratio of ds to dt, i.e.,

(44)

This velocity v is called the linear, or circular, velocity of the point M (not to be confused with its angular velocity).

Thus, the linear velocity of a point belonging to a rotating body is equal to the product of the angular velocity of that body and the distance of the point from the axis of rotation. The linear velocity is tangent to the circle described by point M, or perpendicular to the plane through the axis of rotation and the point M. As the value of ω at any given instant is the same for all points of the body, it follows from Eq. (44) that the linear velocity of any point of a rotating body is proportional to its distance from the axis of rotation (Fig.12).

Fig. 12

In order to determine the acceleration of point M, we apply equations

.

Substituting the expression for v from Eq. (44), we obtain

, ,

and finally

, (45)

The tangential acceleration w_t, is tangent to the path (in the direction of the rotation if it is accelerated and in the reverse direction if it is retarded); the normal acceleration w_n is always directed along the radius h towards the axis of rotation (Fig. 13a).

Fig. 13

The total acceleration of point M is

,

or

(46)

The inclination of the vector of total acceleration to the radius of the circle described by the point is specified by the angle μ, given by the equation

.

Substituting the expressions of wτ, and wn from Eqs. (45), we obtain

. (47)

Since at any given instant s and m are each the same for all the points of the body, it follows from Eqs. (46) and (47) that the accelerations of all the points of a rotating rigid body are proportional to their distance from the axis of rotation and make the same angle μ, with the radii of the circles described by them (Fig. 13b).

Eqs. (44)-(47) make it possible to determine the velocity and acceleration of any point of a body if the equation of rotation of the body and the distance of the given point from the axis of rotation is known. With these formulas, knowing the motion of any single point of a body, it is possible to determine the motion of any other point and the characteristics of the motion of the body as a whole.

Comprehension check.

Ex.2. Answer the following questions .

1. What happens when a body rotates? What path is described?

2. What is the linear velocity of a point belonging to a rotating body equal to?

3. What is the linear velocity tangent to, perpendicular to and proportional to?

4. What is the tangential acceleration w_t tangent to?

5. What is the normal acceleration w_n always directed along ?

Ex.3.Say whether the following statements are True or False.

1. When the body rotates, point M describes a circle of radius h in a plane perpendicular to the axis of rotation.

2. The circular velocity of the point M is the same as its angular velocity.

3. The linear velocity is perpendicular to the circle described by point M.

4. The linear velocity of any point of a rotating body is inversely proportional to its distance from the axis of rotation.

5. The normal acceleration w_n is tangent to the path.

6. Knowing the motion of any single point of a body, it is possible to determine the motion of any other point and the characteristics of the motion of the body as a whole.

Ex.4. Match the verbs and their synonyms. Each verb can have more than one synonym. Compose 5 sentences with any of these verbs.

Verbs: Apply, consider, describe, determine, establish, investigate, rotate, substitute.

Synonyms : alternate, examine, portray, believe, explore, depict, think, establish, look into, turn around, create, conclude, illustrate, revolve, use, decide, set up, regard as, replace with.

Ex.5. Complete the sentences with the following prepositions:

From, along, as, to, towards, for, of .

1. The normal acceleration w_n is always directed ……the radius h ……. the axis of rotation.

2. This conclusion follows …… Equation 46.

3. The acceleration of a point of a rotating rigid body is proportional …. its distance ….. the axis of rotation.

4. It is possible to determine the characteristics …… motion of the body ….a whole.

5. This point belongs …..a rotating body.

6. This value is the same …….all the points of the body.

Ex.6. Link two short sentences into one longer sentence connecting them with the following words: Since, if, when, in order to, as, while, hence.

1. The body rotates. Point M describes a circle.

2. We need to determine the acceleration of a point. We should apply this equation.

3. The angular velocity increases in magnitude. The rotation is accelerated.

4. The distance between the points of a rigid body does not change. In rotational motion all points of the body on the axis of rotation are motionless.

5. The tangential component of acceleration is equal to the rate of change of a particle speed. The normal component is equal to the square of the speed divided by the radius of curvature of the path at point P.

6. In rotational motion all points of the body on the axis of rotation are motionless. All the other points of the body describe circular paths.

7. The acceleration of a particle lies in the osculating plane. The projection of vector on the binormal is zero.

Ex.7 . Translate the following phrases into English.

Рассмотреть характеристики; описывать круг в плоскости; совершать очень малое перемещение; линейная скорость точки; произведение угловой скорости и расстояния; определить ускорение; по направлению вращения; наклон вектора к радиусу; составлять одинаковый угол.