Unit 7.

Rotational Motion of a Rigid Body. Angular Velocity and Angular Acceleration.

Learn the following words and word combinations by heart:

angle of rotation	угол вращения
appropriate sign	cоответствующий знак
axis of rotation	oсь вращения
be reduced to	быть уменьшенным до…
clockwise	по часовой стрелке
counterclockwise	против часовой стрелки
it is sufficient to know… inclination of a vector	достаточно знать… наклон ( угол наклона) вектора
infinitesimal	чрезвычайно малый; не  поддающийся  измерению; мельчайший
hence	отсюда; с этих пор; следовательно; в  результате
motionless	неподвижный
opposite sense	противоположное направление
product of	произведение ….
substitute therefore	замещать по этой причине; вследствие этого; таким  образом

Ex.1. Look at Appendices 1 and 2 and read the following mathematical symbols and Greek letters.

φ = φ (t), , , ,

Rotation of a rigid body is such a motion in which there are always two points of the body (or body extended) which remain motionless (see Fig.10). The line AB through these fixed points is called the axis of rotation.

Since the distance between the points of a rigid body does not change, it is evident that in rotational motion all points of the body on the axis of rotation are motionless, while all the other points of the body describe circular paths in the planes which are perpendicular to the axis of rotation and the centres of which lie on it.

To determine the position of a rotating body, let us pass two planes through the axis of rotation Az: plane I, which is fixed, and plane II through the rotating body and rotating with it (Fig. 10). The position of the body at any instant will be fully specified by the angle φ between the two planes, taken with the appropriate sign, which we shall call the angle of rotation of the body. We shall consider the angle positive if it is laid off counterclockwise from the fixed plane by an observer looking from the positive end of axis Az, and negative if it is laid off clockwise. Angle φ is always measured in radians.

The position of a body at any instant is completely specified if we know the angle φ as a function of time t, i.e.,

φ = φ (t). (36)

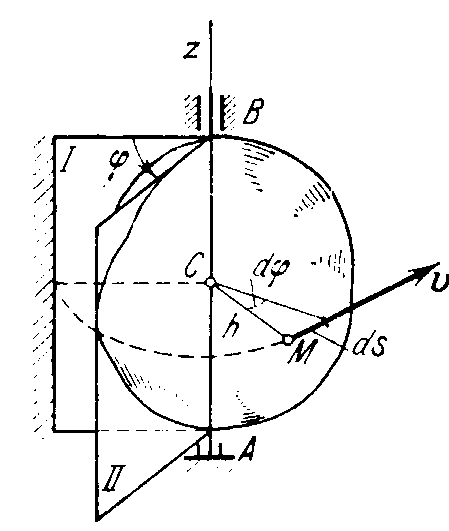
Fig. 10

Eq. (36) describes the rotational motion of a rigid body.

The principal kinematic characteristics of the rotation of a rigid body are its angular velocity and angular acceleration .

If in an interval of time ∆t = t₁ – t a body turns through an angle ∆ φ = φ ₁- φ, the average angular velocity of the body in the given time interval is

.

The angular velocity of a body at a given time t is the value towards which tends when the time interval ∆t tends to zero:

or . (37)

Thus, the angular velocity of a body at a given time is equal in magnitude to the first derivative of the angle of rotation with respect to time. Eq. (37) also shows that the value of is equal to the ratio of the infinitesimal angle of rotation d φ to the corresponding time interval dt. The sign of specifies the direction of the rotation. It will be noticed that >0 when the rotation is counterclockwise, and <0 when the rotation is clockwise. The dimension of angular velocity, if the time is measured in seconds, is

,

as the radian is a dimensionless unit.

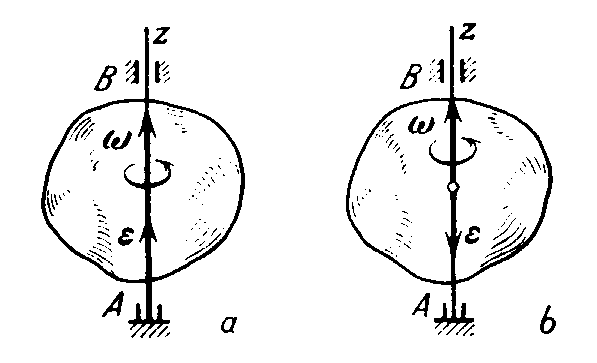
Fig. 11

The angular velocity of a body can be denoted by a vector of magnitude along the axis of rotation of the body in the direction from which the rotation is seen as counterclockwise (see Fig. 11). Such a vector simultaneously gives the magnitude of the angular velocity, the axis of rotation, and the sense of rotation about that axis.

Angular acceleration characterizes the time rate of change of the angular velocity of a rotating body.

If in a time interval ∆t=t1–t the change of angular velocity of a body is , the average angular acceleration of the body in that interval of time is .

The angular acceleration at a given time t is the value towards which tends when the time interval ∆t tends to zero. Thus,

,

or, taking into account Eq. (37)

. (38)

Thus, the angular acceleration of a body at a given time is equal in magnitude to the first derivative of the angular velocity, or the second derivative of the angular displacement, of the body with respect to time. The dimension of angular acceleration is .

If the angular velocity increases in magnitude, the rotation is accelerated, if it decreases, the rotation is retarded. It will be readily noticed that the rotation is accelerated when and are of the same sign and retarded when they are of different sign.

By analogy with angular velocity, the angular acceleration of a body can be denoted by a vector along the axis of rotation. The direction of coincides with that of when the rotation is accelerated (Fig. 11a), and is of opposite sense when the rotation is retarded (Fig. 11b).

Comprehension check.

Ex.2. Answer the following questions .

1. What is a rotation of a rigid body?

2. What line is called the axis of rotation?

3. What points of a body are motionless in rotational motion?

4. What points of a body describe circular paths in rotational motion?

5. When is the angle φ positive and when is it negative?

6. How is the angle φ measured?

7. What definition can we give to an angular velocity of a body?

8. When is >0 and when is <0?

Ex.3. Put the questions to the following answers.

1. It characterizes the time rate of change of the angular velocity of a rotating body.

2. It is equal in magnitude to the first derivative of the angular velocity.

3. The rotation is accelerated.

4. The rotation is retarded.

5. By a vector .

6. Their directions coincide.

Ex.4. Complete the following sentences with the information from the text.

1. In rotational motion all points of the body are motionless on………..

2. We should pass …… through the axis of rotation in order to ……...

3. The position of the body at any instant will be fully specified by……

4. The second plane passes through ….

5. Angular acceleration characterizes……

Ex.5. Complete the sentences with the following prepositions:

By, between, at, along, of, through, from, about, to, in.

1. This plane is perpendicular ……the axis of rotation.

2. Let’s pass the plane ……… the axis of rotation.

3. The position of the body …… any instant will be specified ……the angle φ …….the two planes.

4. Angle φ is always measured …….radians.

5. The angular velocity of a body can be denoted ….. a vector of magnitude ……. the axis of rotation of the body ….. the direction ……..which the rotation is seen as counterclockwise.

6. This vector gives the sense or rotation ……..that axis.

Ex.6. Match the terms and their definitions.

1	angle	a	the action of turning around a fixed point
2	fixed	b	a completely flat surface in geometry
3	instant	c	not moving at all
4	magnitude	d	the space between two straight lines or surfaces that touch or cross each other, measured in degrees
5	motionless	e	a moment
6	plane	f	a picture, symbol that has a particular meaning
7	rotation	g	firmly fastened to a particular position
8	sign	h	greatness of size or importance

Ex.7. Match : 1) the adjectives in the left column with the nouns in the right one;