Unit 6. Translational Motion of a Rigid Body

Learn the following words and word combinations by heart:

analysis of translational motion	анализ поступательного движения
arbitrary point	произвольная точка
assume	полагать, предполагать
be evident	являться очевидным, явным
coincide	совпадать
consider	рассматривать
consideration (of)	рассмотрение, изучение чего-либо
definition	определение
differentiate	различать; отличать; дифференцировать; разграничивать
evidently	очевидно
in particular	в частности, в особенности
it follows from an equation	из уравнения следует….
regard all solids as remain	рассматривать все твердые тела как … оставаться, пребывать
superimpose	накладывать друг на друга, совмещать; перекрывать
translation	поступательное движение

Ex.1. Look at Appendix 1 and read the following mathematical symbols.

, ,

In kinematics, as in statics, we shall regard all solids as rigid bodies, i.e., we shall assume that the distance between any two points of a body remains the same during the whole period of motion.

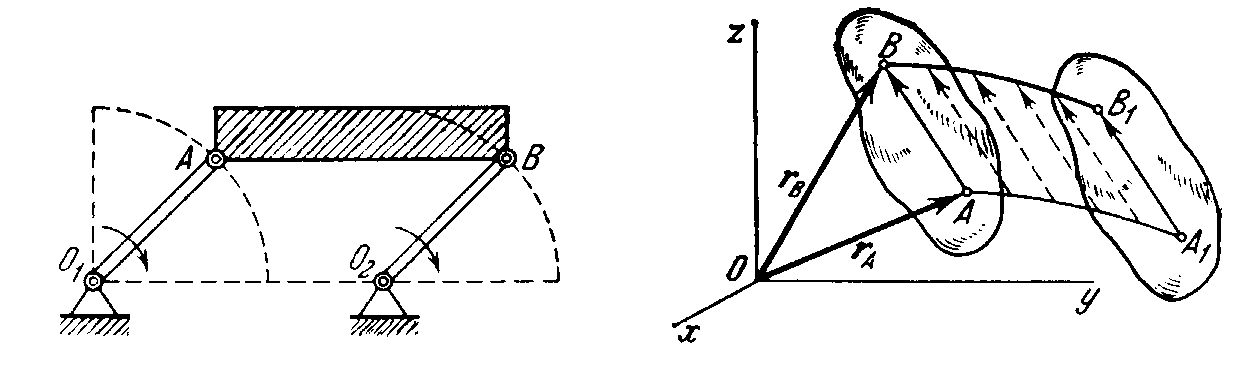
Fig. 8 Fig. 9

Problems of kinematics of rigid bodies are basically of two types: (1) definition of the motion and analysis of the kinematics characteristics of the motion of a body as a whole; (2) analysis of the motion of every point of the body in particular. We shall begin with the consideration of the motion of translation of a rigid body.

Translation of a rigid body is such a motion in which any straight line through the body remains continually parallel to itself.

Translation should not be confused with rectilinear motion. In translation the particles of a body may move on any curved paths.

The properties of translational motion are defined by the following theorem: In translational motion, all the particles of a body move along similar paths (which will coincide if superimposed) and have at any instant the same velocity and acceleration. To prove the theorem, consider a rigid body translated with reference to a system of axes Oxyz. Take two arbitrary points A and B on the body whose positions at time t are specified by radius vectors and (Fig. 9). Draw a vector joining the two points. It is evident that

(35)

The length of is constant, being the distance between two points of a rigid body, and the direction of is constant by virtue of the translational motion of the body. Thus, the vector is constant throughout the motion of the body ( = const.). It follows then from Eq.(35) (and the diagram) that the path of particle B can be obtained by a parallel displacement of all the points of the path of particle A through a constant vector . Hence, the paths of particles A and B are identical curves, which will coincide if superimposed.

To determine the velocities of points A and B, we differentiate both parts of Eq. (35) with respect to time. We have

.

But the derivative of the constant vector is zero while the derivatives of vectors and with respect to time give the velocities of points A and B. Thus we find that

,

i.e., at any instant the velocities of points A and B are equal in magnitude and direction.

Again, differentiating both sides of the equation with respect to time, we obtain

or .

Hence, at any instant the accelerations of A and B are equal in magnitude and direction.

As points A and B are arbitrary, it follows that the paths and the velocities and accelerations of all the points of a body at any instant are the same, which proves the theorem.

It follows from the theorem that the translational motion of a rigid body is fully described by the motion of any point belonging to it. Thus, the analysis of translational motion of a rigid body is reduced to the methods of particle kinematics examined before.

The common velocity of all the points of a body in translational motion is called the velocity of translation, and the common acceleration w is called the acceleration of translation. Vectors and can, obviously, be shown as applied at any point of the body.

Comprehension check.

Ex.2. Answer the following questions .

1. What does a rigid body imply? What are its main characteristics?

2. What are the problems of kinematics of rigid bodies?

3. What is translation?

4. What is the difference between translation and rectilinear motion?

5. What theorem defines the properties of translational motion?

6. Why is the length and direction of constant?

7. What definitions can we give to the velocity and the acceleration of translation?

Ex.3 .Say whether the following statements are True or False.

1. The distance between any two points of a rigid body constantly changes during the whole period of motion.

2. Analysis of the motion of every point of the body in particular is one of the problems of kinematics of rigid bodies.

3. In translational motion, all the particles of a body move along similar paths.

4. Translation is another word for denoting rectilinear motion.

5. The accelerations of points A and B of a rigid body change in magnitude and direction all the time.

6. Translational motion of a rigid body is fully described by the motion of any point belonging to it.

7. In translational motion, if we superimpose the paths along which all the particles of a body move, the paths will be different.

Ex.4. Match the terms and their definitions.

1	body	a	a quality or feature of sth that is typical of it and easy to recognize
2	curved	b	formed or moving in a straight line or consisting of straight lines
3	characteristic	c	a quality or power that belongs naturally to sth
4	determine	d	the science dealing with the forces that produce balance in objects that are not moving
5	path	e	an object that is separated from other objects
6	property	f	a firm object or substance that has a fixed shape, unlike a gas or liquid
7	rectilinear	g	having a shape that is rounded and not straight
8	solid	h	the direction or line along which sb or sth moves
9	statics	i	to find out the exact details or fact about sth

Ex.5. Fill in the words from the text.

1. In kinematics we shall regard all solids as ….. bodies.

2. In translational motion, all the particles of a body move …. ……. paths.

3. Let’s take two ……points A and B on the body.

4. The length of is ……., because it is the distance between ……. …… of a rigid body.

5. The paths of particles A and B are …. …….. They will …… if superimposed.

Ex.6. Complete the following table:

Noun	Verb	Adjective
assumption
	define
		analytical
	move
consideration
		translational
straightness
		curved /curvy
	coincide

Ex.7. Translate into English.

1. Траектория, скорость и ускорение всех точек твердого тела одинаковы в любой момент времени.

2. Скорость поступательного движения - это общая скорость всех точек тела при поступательном движении.

3. Расстояние между любыми 2 точками твердого тела не изменяется в процессе перемещения.

4. Поступательное и прямолинейное движение являются различными типами движения.

5. Тело перемещается относительно системы координат.