Unit 5. Tangential and Normal Accelerations of a Particle.

Learn the following words and word combinations by heart:

by virtue of the definition be determined from	на основании определения быть определенным из
denote	означать, обозначать
draw a line through a point include	провести линию через точку включать
instant of time	момент времени
in terms of	с точки зрения…
limits of each of the cofactors inside the brackets	пределы каждого алгебраического дополнения в скобках
multiply	умножить
product of….by right –hand side of the equation stationary coordinate axes	произведение …на правая сторона уравнения неподвижная система координат
sweep around	колебаться, развертываться вокруг
sweep of tangent	колебание, развертывание касательной
value of the velocity	значение скорости

Ex.1. Look at Appendix 1 and read the following mathematical symbols and Greek letters.

τ, w, Δφ, ., sin , wn>0,

We can already compute the acceleration vector according to its projections on stationary coordinate axes Oxyz. In the natural method of describing motion, vector is determined from its projections on a set of coordinate axes Mτ nb whose origin is at M and who move together with the body (Fig. 6).

The acceleration of a particle lies in the osculating plane, i.e., plane Mτn, hence the projection of vector on the binormal is zero (wb = 0).

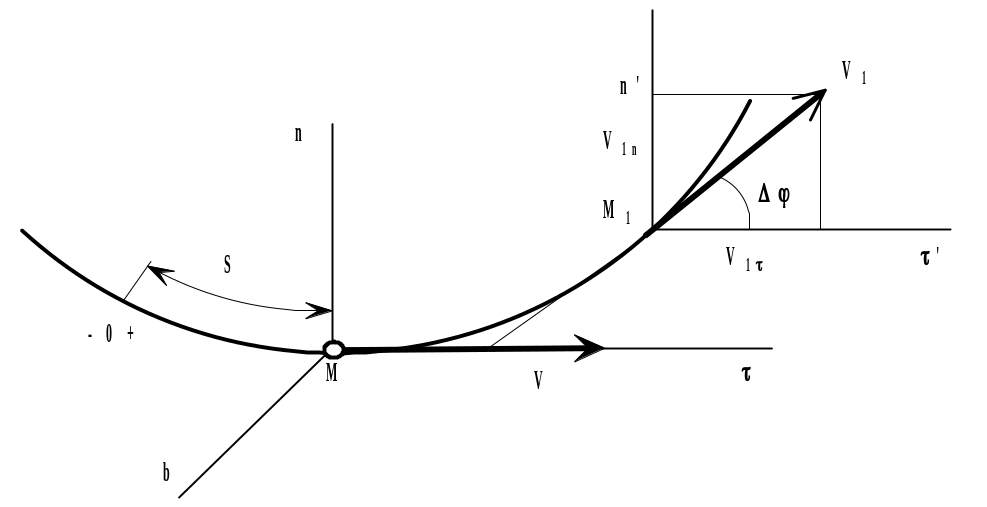
Fig. 6

Let us calculate the projection of on the other two axes. Let the particle occupy a position M and have a velocity at any time t, and at time t₁=t+Δt let it occupy a position M₁ and have a velocity . Then, by virtue of the definition,

Let us now express this equation in terms of the projections of the vectors on the axes Mτ and Mn through point M (see Fig. 6). From the theorem of the projection of a vector sum (or difference) on an axis we obtain:

, .

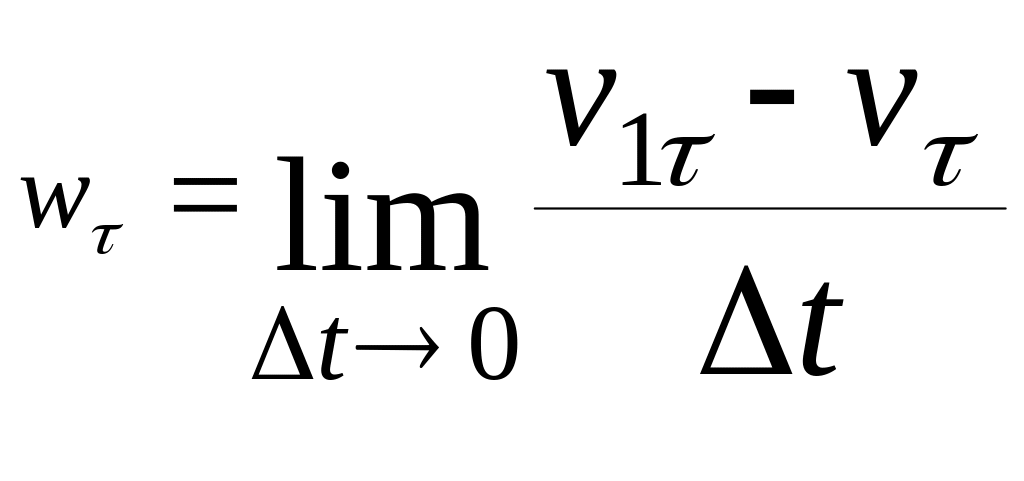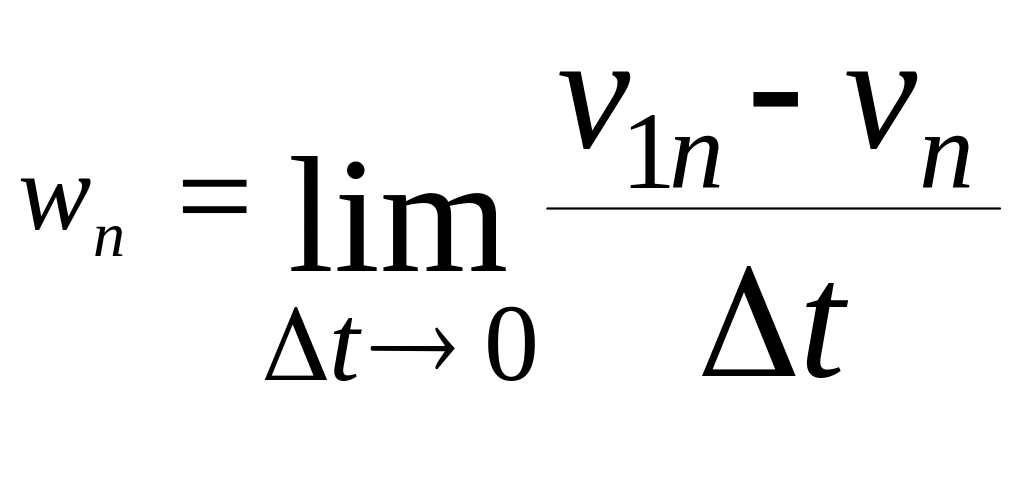Noting that projections of a vector on parallel axes are equal, draw through point M₁ axes Mτ' and Mn' parallel to Mτ and Mn respectively, and denote the angle between the direction of vector and the tangent Mτ by the symbol Δφ. This angle between the tangents to the curve at points M and M1 is called the angle of contiguity.

It will be recalled that the limit of the ratio of the angle of contiguity Δφ to the arc = s defines the curvature k of the curve at the point M. As the curvature is the inverse of the radius of curvature  at M, we have:

.

From the diagram in Fig. 6, we see that the projections of vectors and on the axes M and Mn are

v = v, vn = 0,

v1 = v1 cos , v1n = sin ,

where v and v₁ are the numerical values of the velocity of the particle at instants t and t₁. Hence,

, .

It will be noted that when , point M1 approaches M indefinitely, simultaneously , and .

Hence, taking into account that , we obtain for w the expression

.

We shall transform the right-hand side of the equation for wn in such a way so that it includes ratios with known limits. For this purpose, multiplying the numerator and denominator of fraction under the limit sign by s, we find:

, (23)

since, when , the limits of each of the cofactors inside the brackets are as follows:

.

Finally we obtain

, . (24)

We have thus proved that the projection of acceleration of a particle on tangent to the path is equal to the first derivative of numerical value of the velocity, or the second derivative of the displacement (the arc coordinate) s, with respect to time; the projection of the acceleration on the principal normal is equal to the second power of the velocity divided by the radius of curvature of the path at the given point of curve, the projection of acceleration on the binormal is zero (wb = 0). This is an important theorem of particle kinematics.

When particle M is moving in one plane, the tangent M sweeps around the binormal Mb with an angular velocity . By introducing this quantity into Eq. (23) we can obtain one more equation for calculating wn that is frequently used in practice:

Wn = v (24.1)

i.e. normal acceleration equals the product of a particle’s velocity by angular velocity of the sweep of tangent to the path.

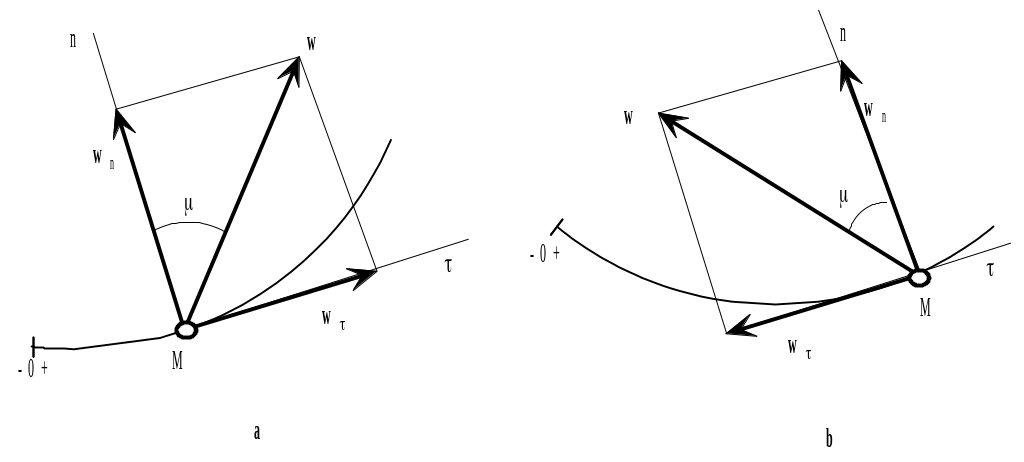
Fig. 7

Lay off vectors and , i.e. the normal and tangential components of the acceleration, along the tangent M and the principal normal Mn, respectively (Fig. 7). The component is always directed along the inward normal, as wn>0, while the component can be directed either in the positive or in the negative direction of axis M, depending on the sign of the projection w (see Figs. 7 a and b).

The acceleration vector is the diagonal of a parallelogram constructed with the components and as its sides. As the components are mutually perpendicular, the magnitude of vector and its angle  to the normal Mn are given by the equations:

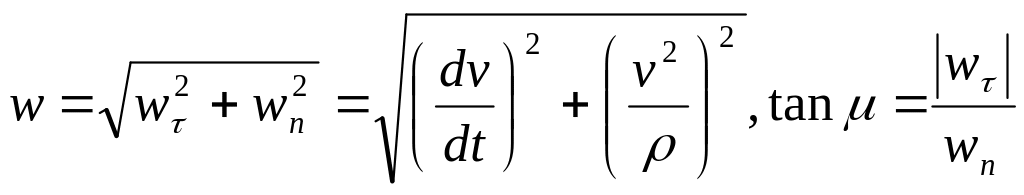(25)

Thus, if the motion of a particle is described by the natural method and the path (and, consequently, the radius of curvature at any point) and the equations of motion (20) are known, from Eqs. (22), (24), and (25) we can determine the magnitude and direction of the velocity and acceleration vectors of the particle for any instant.

Comprehension check.

Ex.2. Put the questions to the following answers.

1. It happens when Δt tends to zero.

2. To the first derivative of numerical value of the velocity.

3. It sweeps around the binormal Mb with an angular velocity .

4. It equals the product of a particle’s velocity by angular velocity of the sweep of tangent to the path.

5. Along the inward normal.

6. Either in the positive or in the negative direction of axis M.

Ex.3 .Say whether the following statements are True or False.

1. The curvature is the inverse of the radius of curvature at the definite point.

2. The projection of acceleration of a particle on tangent to the path is equal to the second power of the velocity divided by the radius of curvature of the path at the given point of curve.

3. Normal acceleration equals sum of a particle velocity and angular velocity of the sweep of tangent to the path.

4. The component is always directed along the inward normal.

5. The acceleration vector is the diagonal of a parallelogram constructed with the components and as its sides.

Ex.4. Complete the following sentences with the information from the text.

1. The limit of the ratio of the angle of contiguity…

2. V and V₁ are the numerical values of …

3. The projection of the acceleration on the principal normal is equal …

4. Noting that projections of a vector on parallel axes are equal, draw…

5. When particle M is moving in one plane, the tangent…

Ex.5. Match the words from the left column with those in the right one. The words in the right column can be used more than once.

1	stationary	a	of contiguity
2	method of	b	with known limits
3	set of	c	the definition
4	lie	d	coordinate axes
5	projection on	e	in terms of
6	by virtue of	f	in the osculating plane
7	express	g	the curvature of the curve
8	the angle	h	describing motion
9	define	i	of curvature
10	radius
11	ratio

Ex.6. Fill in the corresponding verbs in a suitable form and particles .