Тема 3. Побудова лінійної множинної регресійної моделі
Лінійна множинна регресія. Математична модель.
У багатьох випадках на результативну ознаку впливає не один, а кілька факторів. Між факторами існують складні взаємозв'язки, тому їхній вплив на результативну ознаку є комплексним, а не просто сумою ізольованих впливів.
Багатофакторний аналіз дає змогу оцінити міру впливу на досліджуваний результативний показник кожного із введених у модель факторів при фіксованому положенні на середньому рівні інших факторів. Важливою умовою є відсутність функціонального зв'язку між факторами.
Математично завдання зводиться до знаходження аналітичного виразу, який якнайкраще відображував би зв'язок факторних ознак з результативною, тобто знайти функцію:
=f(X1,X2,X3,...
,Хk).
Найскладнішою проблемою є вибір форми зв'язку аналітичного виразу. На підставі чого за наявними факторами визначають результативну ознаку-функцію. Ця функція має краще за інші відображати реальні зв'язки між досліджуваним показником і факторами. Емпіричне обґрунтування типу функції за допомогою графічного аналізу зв'язків для багатофакторних моделей майже непридатне. Форму зв'язку можна визначати добиранням функцій різних типів, але це пов'язане з великою кількістю зайвих розрахунків. Зважаючи на те, що будь-яку функцію багатьох змінних шляхом логарифмування або заміни змінних можна звести до лінійного вигляду, рівняння множинної регресії можна виразити у лінійній формі:
Y= 0 + 1X1 +2X2 + …+kXk.
Інформація про значення Y, X1,..., Xn міститься у відповідних статистичних даних, n спостереженнях (вимірюваннях) кожного показника.
Кожний коефіцієнт рівняння вказує на ступінь впливу відповідного фактора на результативний показник при фіксованому положенні решти факторів, тобто як зі зміною окремого фактора на одиницю змінюється результативний показник Вільний член рівняння множинної регресії економічного змісту не має.
Запишемо математичну модель множинної лінійної регресії, основану на незалежності ВВ (факторів) Xj, j=1…k, які мають нормальний розподіл і за припущенням впливають на залежну змінну Y. Це дозволяє провести статистичний аналіз, тобто записати інтервальні оцінки для параметрів k множинної функції регресії і перевірку статистичних гіпотез про значення цих параметрів, основану на t – розподілі Стьюдента.
Номер досліду |
Результати досліду |
||||
X1 |
X2 |
... |
Xk |
Y |
|
1 |
x11 |
x12 |
... |
x1k |
y1 |
2 |
X21 |
X22 |
... |
X2k |
y2 |
... |
... |
... |
... |
... |
... |
n |
Xn1 |
Xn2 |
... |
Xnk |
yn |
Позначимо X – (n(k+1)) - мірна таблиця незалежних змінних (X01 – змінна при 0).
X=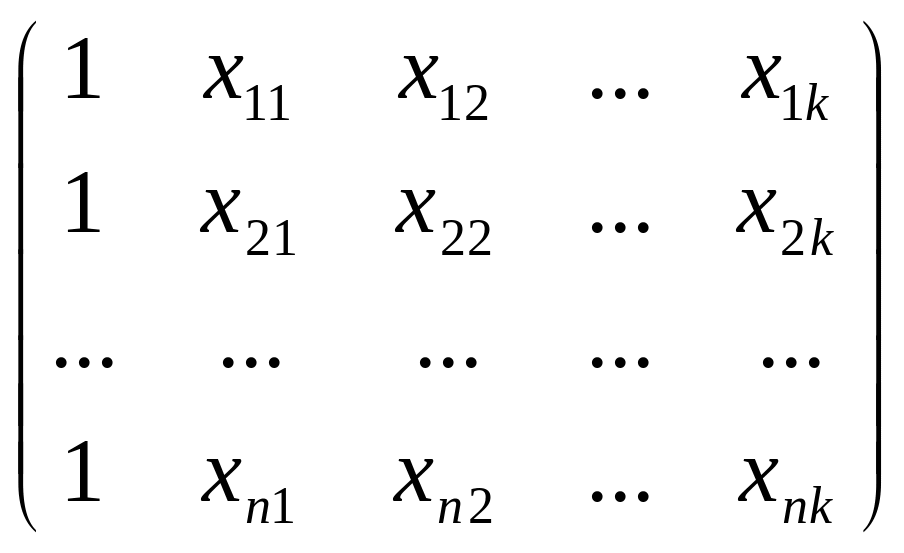
; y=
;
=
; 
.
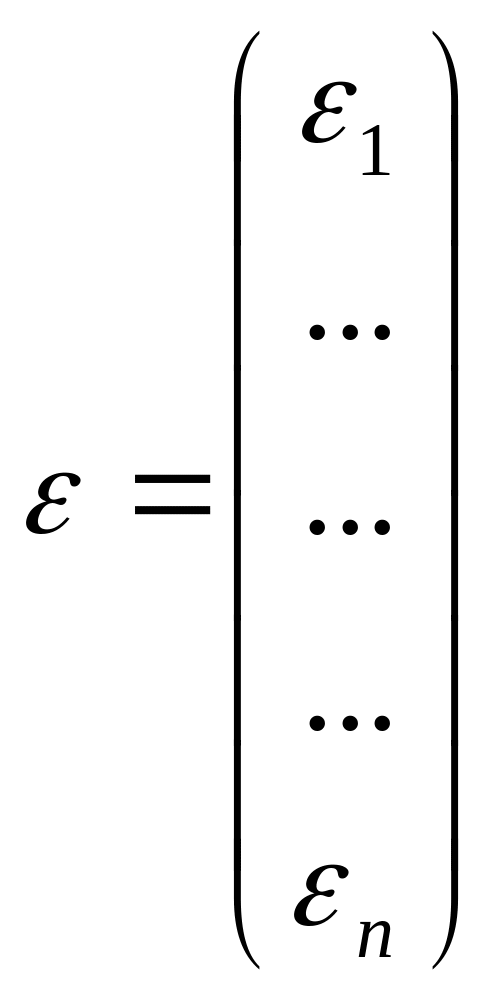де Y – n - мірний вектор – стовпець спостережень залежної змінної, - (k+1)-мірний стовпець параметрів, - n – мірний випадковий вектор, складові якого є випадковими похибками.
Припустимо:
Y= X+ , де X – матриця спостережень незалежних змінних.
Випадковий вектор – стовпець похибок (n – мірна ВВ) визначається густиною ймовірності:
f()=
,
тобто
має нормальний розподіл з нульовим
вектором математичних очікувань і
ковариційно – дисперсійною матрицею
,
де Е
– одинична матриця порядку n.
Матриця спостережень X незалежних змінних має ранг rang(X)=k+1 n.
Умова 1 означає лінійну залежність між змінною Y і змінними (факторами) X, які впливають на розсіювання Y. Дана лінійна залежність справедлива з точністю до випадкового j.
Умова 2 означає, що випадкові похибки j є незалежними випадковими величинами, які мають нормальний розподіл N(0,) з нульовим математичним очікуванням і одним і тим же середнім квадратичним відхиленням . Як правило, дисперсія 2 випадкового j невідома, то залишається невідомою і ковариційно – дисперсійна матриця випадковго вектора похибки j. Тому її необхідно оцінити.
Умова 3 означає, що матриця спостережень X не є випадковою. Її стовпці складають систему (k+1) лінійно – незалежних векторів, причому число стрічок матриці не менше числа її стовпців, тобто не менше числа параметрів j.
Із умов 1-3 слідує: M(|X)=0, M(Y|X)=X, (Y|X)=2E,
де M(|X) – умовне математичне очікування доданку при фіксованому векторі спостережень незалежних змінних.
Необхідно оцінити вектор параметрів лінійного рівняння регресії і дисперсію ВВ , побудувати довірчі інтервали для параметрів j, j =0…k, гіперплощини регресії, перевірити адекватність моделі (множинна лінійна регресія) даним експерименту.
Параметри
j,
j
=0…k,
оцінюються за МНК, при умові, що сума
квадратів відхилень спостережуваних
значень залежної змінної Y
від
гіперплощини регресії X
мінімальна.
Тобто необхідно підібрати вектор оцінок
b,
при
якому функція S,
яка
визначається рівністю S=
досягала б мінімуму; =Y-
- емпіричне
рівняння регресії.
Формули для обчислення оцінок параметрів множинної лінійної регресії:
.
Обернена симетрична матриця існує в силу умови 3 математичної моделі.
Незміщена оцінка дисперсії 2 ВВ :
s2=
.
Ковариційно – дисперсійна матриця вектора оцінок
:
(b)=
2(XTX)-1.Довірчий інтервал для довільного коефіцієнта j:
,
де
- квантиль розподілу Стьюдента, відповідний
довірчій ймовірності P=1-
і
числу степеней вільності =n-k-1;
bj
– точкова оцінка j
- складової
вектора
;
sbj=s
,
– -j-ий
діагональний елемент ковариційно-дисперсійної
матриці
.
Коефіцієнт множинної кореляції R, який вимірює степінь тісноти лінійної залежності ВВ Y від факторів Xj:
R=
,
де
=2/D(Y),
-
коефіцієнт сходження;
2
– дисперсія
випадкового доданку ,
D(Y)
– дисперсія
ВВ Y.
0R1.
Якщо
R=0,
то
змінна Y
лінійно
незалежна від змінних X,
якщо
R=1,
то
змінна Y
знаходиться
в лінійній функціональній залежності
від X.
Оцінка множинного коефіцієнта кореляції називається емпіричним коефіцієнтом множинної кореляції:
В матричній формі:
Щоб перевірити, який з факторів Xj, j=1…k не має суттєвого впливу на Y, перевіряють нульову гіпотезу про те, що коефіцієнт регресії j при факторі Xj рівний нулю, тобто гіпотезу H0: j=0 проти гіпотези H1: j0. Якщо гіпотеза H0 відхиляється, то вважається, що фактор Xj має вплив на Y. Якщо гіпотеза H0 приймається, то вважається, що фактор Xj не має суттєвого впливу на Y.
Перевірка гіпотези H0 проти гіпотези H основана на обчисленні статистики (критерію Стьюдента): t=bj/sbj. Статистика t при умові справедливості гіпотези H0: j=0 має розподіл Стьюдента з v=n-k-1 степенями вільності. Із таблиць Стьюдента по заданому рівні значущості (як правило =0,05) і числу степенем вільності v=n-k-1 знаходять критичне значення статистики t табл. Якщо |tнабл|>tтабл, H0 гіпотеза відхиляється, якщо |tнабл|tтабл, то приймається. Незначні фактори Xj, при яких коефіцієнти j несуттєво відрізняються від нуля, необхідно із моделі виключити, тобто побудувати заново лінійну множинну регресій ну модель з меншим числом факторів.
Як
правило модель вважається адекватною,
якщо
,
тобто,
.
Якщо
отримаємо
,
має
зміст побудувати нелінійну модель.
Приклад
Стаж роботи, тарифний розряд і денна заробітна плата десяти робітників підприємства характеризуються певними даними (табл.) Треба встановити залежність заробітної плати Y від двох факторів, стажу роботи робітників X1, і тарифного розряду Х2. Заповнимо розрахункову таблицю.
Припустимо, що між Y i факторами X1 X2 є лінійний зв’язок (з точністю до ВВ ), запишемо:
Y=0+1X1+2X2+,
рівняння регресії:
=b0+b1X1+b2X2,
де
Y
– фактичне
значення заробітної плати,
- розрахункове
значення заробітної плати; 0,
1,
2
– параметри
моделі, які треба оцінити; b0,
b1,
b2
– відповідні оцінки параметрів моделі,
Х=
Y=
.
=
.
=
.
=
.
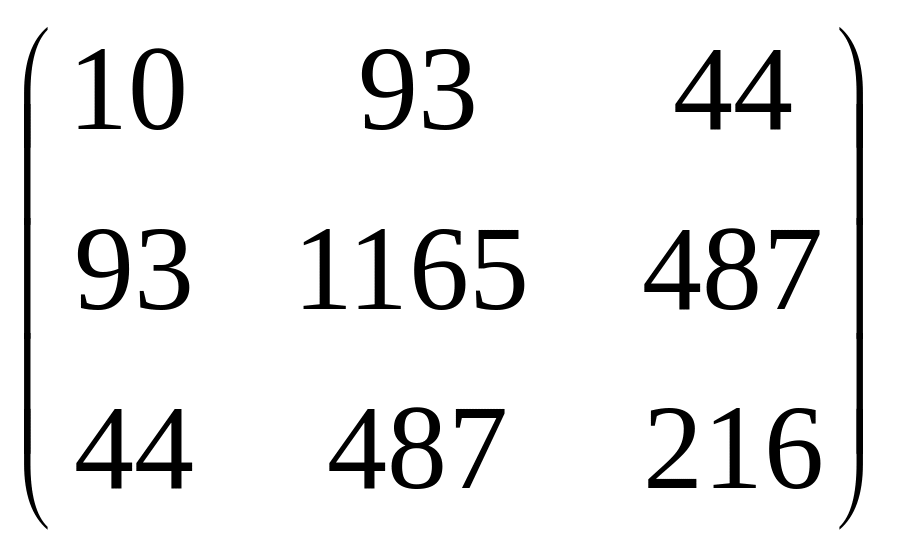точкова
оцінка вектора
:
=
.
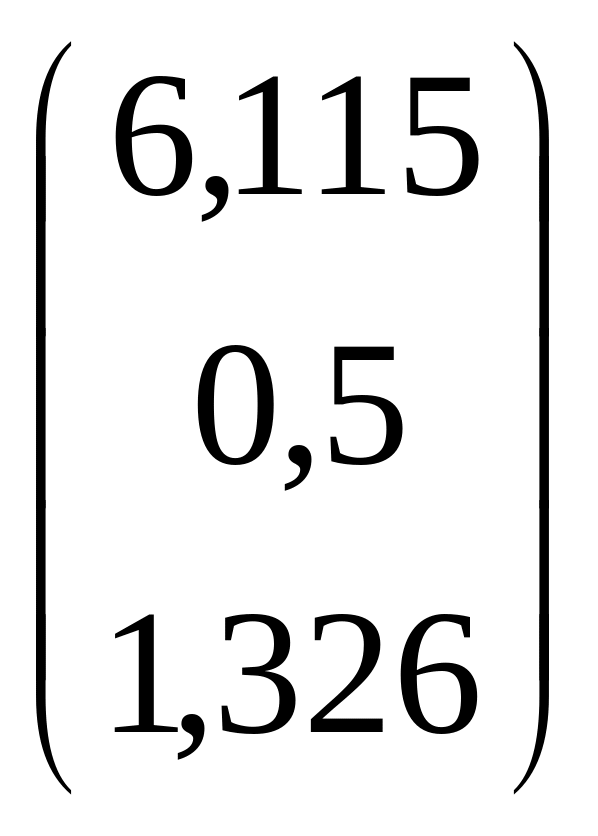Множинна лінійна функція регресії з врахуванням оцінок коефіцієнтів моделі:
=6,115+0,5x1+1,326x2.
Точкова оцінка коефіцієнтів означає, що із збільшенням стажу роботи робітника на 1 рік денна заробітна плата підвищується на 0,5 грн. (при інших незмінних умовах), а при підвищенні тарифного розряду на одиницю денна заробітна плата зростає на 1,326 грн. (при інших незмінних умовах).
Підставивши в рівняння значення X1 і Х2, отримаємо відповідні значення змінної середньої (остання графа табл. ), які досить близько відтворюють фактичні рівні заробітної плати. Це свідчить про правильний вибір форми математичного вираження кореляційного зв'язку між трьома досліджуваними ознаками.
Однак
на підставі коефіцієнтів регресії не
можна судити, яка з факторних ознак
найбільше впливає на результативну,
оскільки коефіцієнти регресії між собою
непорівняльні, адже їх виражено різними
одиницями. З метою виявлення порівняльної
сили впливу окремих факторів та їхніх
резервів, статистика обчислює часткові
коефіцієнти еластичності
:
де
bі
—
коефіцієнт регресії при і-му
факторі;
— середнє
значення і-го
фактора;
— середнє
значення результативної ознаки;
Часткові коефіцієнти еластичності показують, на скільки процентів у середньому зміниться результативна ознака при зміні на 1% кожного фактора та фіксованому положенні інших факторів.
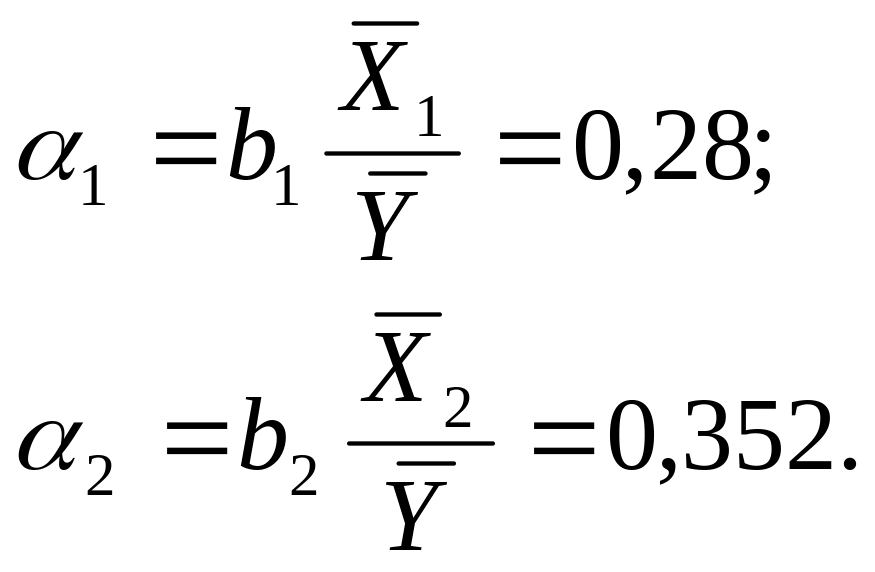
Аналіз часткових коефіцієнтів еластичності показує, що за абсолютним приростом найбільший вплив на заробітну плату робітників має тарифний розряд – фактор Х2, зі збільшенням якого на 1% заробіток підвищується на 0,352 %, а при збільшенні стажу роботи на 1% заробітна плата підвищується на 0,28 %
Загальна еластичність Y від всіх факторів =і =0,632 показує, що денна заробітна плата збільшиться на 0,63%, якщо одночасно збільшити на 1% всі фактори.
Завдання.
На основі абстрактних статистичних даних про роздрібний товарообіг необхідно побудувати множинну регресійну модель залежності роздрібного товарообігу (Y) від кількості підприємств роздрібної торгівлі (X1), всіх наданих платних послуг (X2) та обсягу укладених угод на біржах (X3).
Перевірити адекватність математичної моделі експериментальним даним (xi,yi).
|
Варіант1 |
|
|
Варіант2 |
||||||
|
X1 |
X2 |
X3 |
Y |
|
|
X1 |
X2 |
X3 |
Y |
1 |
15,86 |
3,48 |
33,25 |
33,18 |
|
1 |
7,38 |
9,48 |
6,37 |
45,91 |
2 |
14,57 |
4,05 |
43,15 |
30,45 |
|
2 |
9,4 |
10,5 |
8,4 |
49,34 |
3 |
15,31 |
5,03 |
41,05 |
37,77 |
|
3 |
11,4 |
11,9 |
9,1 |
52,34 |
4 |
14,85 |
6,26 |
40,65 |
40,59 |
|
4 |
10,25 |
9,08 |
5,8 |
47,95 |
5 |
18,18 |
6,2 |
49,3 |
41,07 |
|
5 |
12,3 |
12,4 |
8,4 |
67,34 |
6 |
19,64 |
7,76 |
56,1 |
44,1 |
|
6 |
11,28 |
20,18 |
15,7 |
70,35 |
7 |
17,22 |
9,06 |
57,6 |
43,65 |
|
7 |
12,49 |
15,67 |
10,4 |
80,25 |
8 |
18,99 |
8,45 |
51,1 |
52,5 |
|
8 |
10,4 |
13,9 |
10,6 |
86,14 |
9 |
21,51 |
9,88 |
60,65 |
52,92 |
|
9 |
11,6 |
14,5 |
11,4 |
91,34 |
10 |
23,7 |
9,56 |
61,95 |
60,6 |
|
10 |
9,8 |
14,7 |
10,1 |
97,34 |
11 |
24,052 |
12,82 |
57,2 |
55,95 |
|
11 |
8,05 |
11,37 |
8,4 |
95,02 |
12 |
24,56 |
11,56 |
59,35 |
57,02 |
|
12 |
10,7 |
19,8 |
9,4 |
110,35 |
13 |
24,27 |
11,58 |
60,21 |
57,52 |
|
13 |
11,8 |
15,9 |
10,8 |
124,69 |
14 |
26,32 |
12,95 |
61,25 |
59,6 |
|
14 |
12,7 |
16,2 |
11,5 |
119,34 |
15 |
25,99 |
12,35 |
63,36 |
61,15 |
|
15 |
13,7 |
16,8 |
9,4 |
134,27 |
16 |
27 |
13,65 |
64,02 |
62,54 |
|
16 |
14,73 |
18,36 |
13,1 |
142,17 |
|
|
|
|
|
|
17 |
14,9 |
17,9 |
12,9 |
147,37 |
|
|
|
|
|
|
18 |
13,01 |
15,27 |
18,4 |
138,05 |
|
Варіант3 |
|
|
Варіант4 |
||||||
|
X1 |
X2 |
X3 |
Y |
|
|
X1 |
X2 |
X3 |
Y |
1 |
9,68 |
13,38 |
8,87 |
51,25 |
|
1 |
8,38 |
9,48 |
6,37 |
39,91 |
2 |
10,1 |
10,5 |
10,9 |
54,68 |
|
2 |
9,4 |
10,4 |
8,4 |
49,34 |
3 |
12,1 |
11,9 |
11,6 |
57,68 |
|
3 |
10,28 |
11,08 |
10,1 |
60,27 |
4 |
10,95 |
12,8 |
8,3 |
53,29 |
|
4 |
10,25 |
9,08 |
5,8 |
47,95 |
5 |
13 |
12,4 |
10,9 |
72,68 |
|
5 |
12,3 |
12,4 |
8,4 |
67,64 |
6 |
11,98 |
12,7 |
18,2 |
75,69 |
|
6 |
11,28 |
20,18 |
15,7 |
70,35 |
7 |
13,19 |
14,4 |
12,9 |
85,59 |
|
7 |
12,49 |
15,67 |
10,4 |
80,25 |
8 |
11,1 |
13,9 |
13,1 |
91,48 |
|
8 |
10,4 |
13,9 |
10,6 |
86,14 |
9 |
12,3 |
14,5 |
13,9 |
96,68 |
|
9 |
11,6 |
14,5 |
11,4 |
91,34 |
10 |
10,5 |
14,7 |
12,6 |
102,68 |
|
10 |
9,8 |
14,7 |
10,1 |
97,34 |
11 |
8,75 |
14,8 |
10,9 |
100,36 |
|
11 |
9,81 |
10,8 |
9,4 |
105,02 |
12 |
11,4 |
9,4 |
11,9 |
115,69 |
|
12 |
10,7 |
1908 |
9,4 |
110,35 |
13 |
12,5 |
15,9 |
13,3 |
130,03 |
|
13 |
11,8 |
15,9 |
10,8 |
124,69 |
14 |
13,4 |
16,2 |
14 |
124,68 |
|
14 |
12,7 |
16,2 |
11,5 |
119,34 |
15 |
14,4 |
16,8 |
11,9 |
139,61 |
|
15 |
13,7 |
16,8 |
9,4 |
134,27 |
16 |
15,43 |
17,5 |
15,6 |
147,51 |
|
16 |
12,08 |
15,2 |
11,5 |
130,21 |
17 |
15,6 |
17,9 |
15,4 |
152,71 |
|
17 |
14,9 |
17,9 |
12,9 |
147,37 |
18 |
13,71 |
18,4 |
20,9 |
143,39 |
|
18 |
13,01 |
15,27 |
18,4 |
138,05 |
|
Варіант5 |
|
|
Варіант6 |
||||||
|
X1 |
X2 |
X3 |
Y |
|
|
X1 |
X2 |
X3 |
Y |
1 |
9,68 |
13,38 |
8,87 |
51,25 |
|
1 |
9,21 |
11,01 |
6,3 |
52,27 |
2 |
10,1 |
10,5 |
10,9 |
54,68 |
|
2 |
9,4 |
10,5 |
8,4 |
49,34 |
3 |
10,98 |
11,9 |
12,6 |
65,61 |
|
3 |
10,28 |
11,08 |
10,1 |
60,27 |
4 |
10,95 |
12,8 |
8,3 |
53,29 |
|
4 |
10,45 |
10,08 |
7,8 |
45,95 |
5 |
13,2 |
12,4 |
10,9 |
72,68 |
|
5 |
12,3 |
12,4 |
8,4 |
67,34 |
6 |
9,98 |
12,7 |
18,2 |
75,69 |
|
6 |
11,28 |
20,18 |
15,7 |
70,35 |
7 |
13,19 |
14,4 |
12,9 |
85,59 |
|
7 |
11,45 |
10,69 |
11,5 |
77,28 |
8 |
11,1 |
13,9 |
13,1 |
91,48 |
|
8 |
10,4 |
13,9 |
10,6 |
86,14 |
9 |
12,3 |
14,5 |
13,9 |
96,68 |
|
9 |
11,6 |
14,5 |
11,4 |
91,34 |
10 |
13,5 |
14,7 |
12,6 |
102,68 |
|
10 |
9,8 |
14,7 |
10,1 |
97,34 |
11 |
10,51 |
14,8 |
11,9 |
110,36 |
|
11 |
9,81 |
10,8 |
9,4 |
105,02 |
12 |
11,4 |
9,4 |
11,9 |
115,69 |
|
12 |
10,7 |
19,8 |
9,4 |
110,35 |
13 |
12,5 |
15,9 |
13,3 |
130,03 |
|
13 |
9,84 |
13,27 |
10,8 |
111,04 |
14 |
13,4 |
16,2 |
14 |
124,68 |
|
14 |
12,7 |
16,2 |
11,5 |
119,34 |
15 |
14,4 |
16,8 |
11,9 |
139,61 |
|
15 |
13,7 |
16,8 |
9,4 |
134,27 |
16 |
12,78 |
17,5 |
14 |
135,55 |
|
16 |
13,08 |
17,2 |
13,5 |
135,21 |
17 |
15,6 |
17,9 |
15,4 |
152,71 |
|
17 |
14,9 |
17,9 |
12,9 |
147,37 |
18 |
13,71 |
18,4 |
20,9 |
141,41 |
|
18 |
14,05 |
15,27 |
20,3 |
141,62 |
|
Варіант7 |
|
|
Варіант8 |
||||||
|
X1 |
X2 |
X3 |
Y |
|
|
X1 |
X2 |
X3 |
Y |
1 |
11,51 |
12,01 |
8,8 |
50,61 |
|
1 |
8,21 |
10,71 |
7,3 |
50,27 |
2 |
10,1 |
10,5 |
10,9 |
54,68 |
|
2 |
9,4 |
10,5 |
8,4 |
49,34 |
3 |
10,98 |
11,9 |
12,6 |
65,61 |
|
3 |
10,28 |
11,08 |
10,1 |
60,27 |
4 |
12,05 |
10,8 |
9,3 |
59,29 |
|
4 |
13,25 |
10,08 |
6,9 |
50,95 |
5 |
13 |
12,4 |
10,9 |
72,68 |
|
5 |
12,3 |
12,4 |
8,4 |
67,34 |
6 |
11,98 |
12,7 |
18,2 |
75,69 |
|
6 |
11,57 |
20,01 |
16,7 |
72,35 |
7 |
12,15 |
14,4 |
14 |
82,62 |
|
7 |
11,45 |
10,69 |
11,5 |
77,28 |
8 |
11,1 |
13,9 |
13,1 |
91,45 |
|
8 |
10,4 |
13,9 |
10,6 |
86,14 |
9 |
12,3 |
14,5 |
13,9 |
96,68 |
|
9 |
11,6 |
14,5 |
11,4 |
91,34 |
10 |
10,5 |
14,7 |
12,6 |
102,68 |
|
10 |
9,8 |
14,7 |
10,1 |
97,34 |
11 |
10,51 |
14,8 |
11,9 |
110,36 |
|
11 |
9,81 |
10,8 |
9,4 |
105,02 |
12 |
11,4 |
9,4 |
11,9 |
115,69 |
|
12 |
10,7 |
19,5 |
9,4 |
110,35 |
13 |
10,54 |
15,9 |
13,3 |
116,38 |
|
13 |
9,84 |
13,27 |
10,8 |
111,04 |
14 |
13,4 |
16,2 |
14,21 |
124,68 |
|
14 |
12,7 |
16,2 |
11,5 |
119,34 |
15 |
14,4 |
16,8 |
11,9 |
139,61 |
|
15 |
13,7 |
16,8 |
9,4 |
134,27 |
16 |
15,78 |
20,5 |
15,31 |
140,55 |
|
16 |
12,08 |
15,2 |
11,5 |
130,21 |
17 |
15,6 |
17,9 |
15,4 |
152,71 |
|
17 |
14,2 |
18,9 |
11,9 |
148,37 |
18 |
14,75 |
18,4 |
22,8 |
146,96 |
|
18 |
14,05 |
15,27 |
20,3 |
141,62 |
|
Варіант9 |
|
|
Варіант 10 |
||||||
|
X1 |
X2 |
X3 |
Y |
|
|
X1 |
X2 |
X3 |
Y |
1 |
10,51 |
14,61 |
9,8 |
55,61 |
|
1 |
8,21 |
10,71 |
7,3 |
47,27 |
2 |
10,1 |
10,5 |
11,9 |
54,68 |
|
2 |
10,37 |
11,08 |
9,8 |
50,25 |
3 |
10,98 |
11,9 |
12,6 |
65,61 |
|
3 |
10,28 |
11,08 |
10,1 |
60,27 |
4 |
10,95 |
12,8 |
8,3 |
55,29 |
|
4 |
10,25 |
9,08 |
5,8 |
47,95 |
5 |
13,8 |
12,4 |
11,9 |
72,68 |
|
5 |
12,3 |
12,4 |
8,4 |
67,34 |
6 |
11,02 |
12,5 |
15,7 |
73,69 |
|
6 |
11,28 |
20,18 |
15,7 |
70,35 |
7 |
12,05 |
14,4 |
14 |
82,62 |
|
7 |
11,45 |
10,69 |
11,5 |
77,28 |
8 |
11,1 |
13,9 |
13,1 |
91,48 |
|
8 |
10,4 |
13,9 |
10,6 |
86,14 |
9 |
12,3 |
14,5 |
13,9 |
96,68 |
|
9 |
11,6 |
14,5 |
11,4 |
91,34 |
10 |
10,5 |
14,7 |
12,6 |
102,68 |
|
10 |
9,8 |
14,7 |
10,1 |
97,34 |
11 |
10,51 |
14,8 |
11,9 |
110,36 |
|
11 |
9,81 |
10,8 |
9,4 |
105,02 |
12 |
11,4 |
9,4 |
11,9 |
115,69 |
|
12 |
8,9 |
15,06 |
8,1 |
99,27 |
13 |
10,54 |
15,9 |
13,3 |
116,38 |
|
13 |
9,04 |
12,27 |
11,8 |
105,04 |
14 |
13,4 |
16,2 |
14 |
124,68 |
|
14 |
12,7 |
16,2 |
11,5 |
119,34 |
15 |
14,4 |
16,8 |
11,9 |
139,61 |
|
15 |
13,7 |
16,8 |
9,4 |
134,27 |
16 |
12,78 |
17,5 |
14 |
135,55 |
|
16 |
12,08 |
15,2 |
11,5 |
130,21 |
17 |
15,74 |
17,5 |
11,3 |
161,71 |
|
17 |
14,9 |
17,9 |
12,9 |
147,37 |
18 |
19,75 |
21,4 |
29,8 |
178,96 |
|
18 |
16,7 |
20,34 |
22,3 |
161,27 |