5. Оцінка достовірності моделі

Стандартна похибка оцінювання за рівнянням регресії (похибка визначення точкових оцінок коефіцієнтів b₀ і b₁) характеризує точність апроксимації вихідних даних лінійною функцією.

де n – кількість спостережень, m – кількість параметрів моделі.

Чим менша величина S_e, тим міцніший зв'язок між змінними y та x (тобто, тим краще підібрана функція регресії відповідає дослідним даним).

Стандартна похибка оцінювання за рівнянням регресії має таку саму одиницю вимірювання, що й початкові дані результуючої змінної (в нашому прикладі – в тис. грн.).

Якщо S²_e=0, то всі фактичні дані збігаються з теоретичними ( ), тобто початкові спостереження лежать на лінії регресії і взаємозв’язок є функціональним. Тоді коефіцієнт кореляції дорівнює одиниці.

Функція СТОШУХ обчислює стандартну похибку регресії.

Для нашого прикладу:

Якщо відстані на кореляційній діаграмі між лініями довіри та лінією регресії дорівнюють подвійній стандартній похибці оцінювання:

то між цими лініями повинно розміщуватися 95 % спостережень. За межами трьох стандартних відхилень від лінії регресії:

практично не повинно бути жодного спостереження.

Інтервальні статистичні оцінки для теоретичних коефіцієнтів b₀ і b₁.

1. Матриця коефіцієнтів системи нормальних рівнянь:

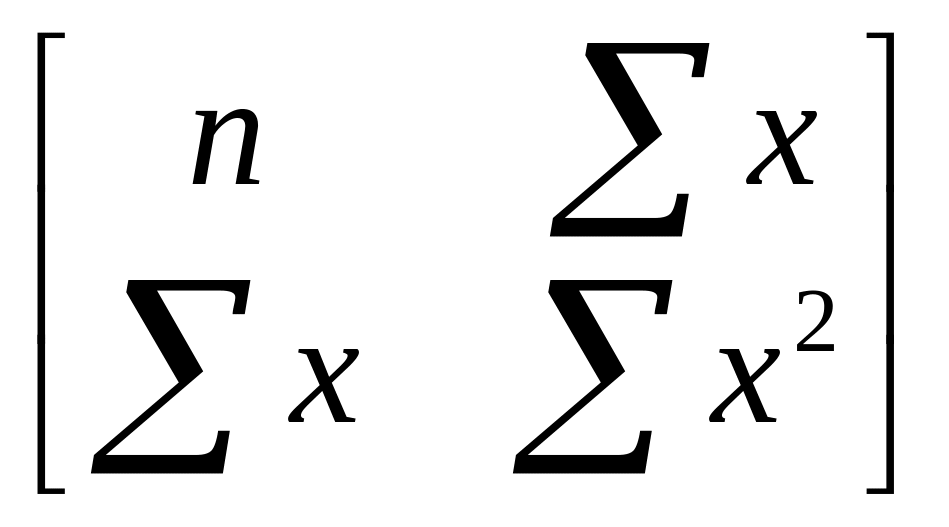
2. Ковариційно-дисперсійна матриця коефіцієнтів рівняння регресії:

3. Стандартна похибка оцінки параметра моделі:

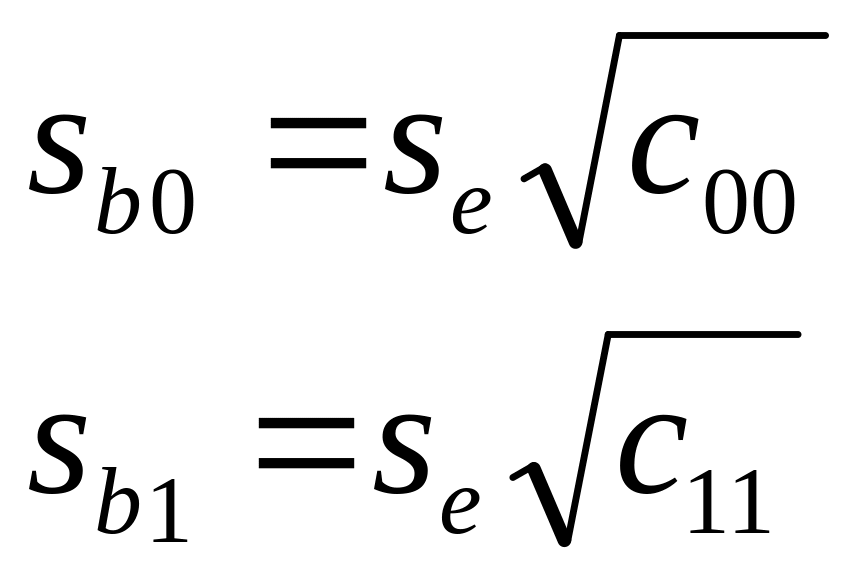де с_00, с₁₁-діагональні елементи ковариційно – дисперсійної матриці.

4. Інтервал, в якому з ймовірністю P=1-=0,95 знаходиться невідоме значення параметра b:

де – критичне значення t-статистики при =n-2 ступенях вільності. Значення визначають з таблиці.

Якщо в границі довірчого інтервалу попадає нуль, тобто нижня границя від’ємна, а верхня – додатна, то оцінюючий параметр приймається нульовим, оскільки він не може одночасно приймати і додатні, і від’ємні значення.

Для нашого прикладу:

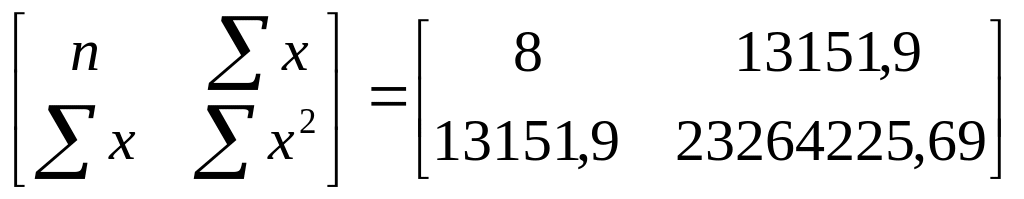
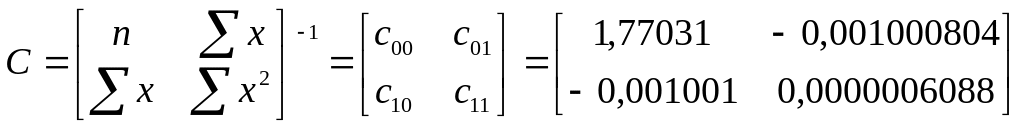
Відповідно

З таблиці Стьюдента для заданої довірчої ймовірності P=1-=1-0,05=0,95 і числа ступенів вільності =n-2=8-2=6 визначимо :

Обчислимо значення t – критерію для параметра b₁:

t₁=

Обчислене значення статистики порівнюємо з критичним значенням t- розподілу з n-k ступенями вільності ( ), знайденим за таблицями Стьюдента.

Якщо , то відповідна оцінка параметра моделі b є достовірною. Отже, з ймовірністю 95% гіпотезу про те, що коефіцієнт регресії генеральної сукупності дорівнює нулю, відхиляємо на основі нашої вибірки.

Оскільки для нашого прикладу фактичне значення t- статистики є більшим за табличне значення ( ), то параметр b₁ не випадково відрізняється від нуля, а є статистично значимий. Отже, з ймовірністю 95 % коефіцієнт рівняння b₁ лінійної регресії за межами діапазону, по якому були зібрані експериментальні дані буде відмінний від нуля.

На основі t-критерію та стандартної похибки можна побудувати довірчі інтервали для параметра

Інтервальні оцінки коефіцієнтів регресії:

Отже, з ймовірністю 95 % в інтервалі [0,780;0,880] буде знаходитися оцінювальний теоретичний параметр .

Отже, якщо наші спостереження (прибуток і дохід) є результатом випадкового вибору з деякої генеральної сукупності, розподіленої за законом Гауса, то з ймовірністю P=0,95 можна стверджувати, що істинний коефіцієнт регресії набуватиме значень не менших від 0,780 і не більших від 0,880. Тобто, кожна тисяча гривень доходу сприятиме приросту прибутку не менше, ніж на 0,780 і не більше, ніж на 0,880 тис грн.

Коефіцієнт кореляції

Коефіцієнти різних рівнянь регресії при неоднакових одиницях вимірювання результуючої або факторної змінної не можна порівнювати. На практиці часто виникає необхідність порівняння двох чи декількох рівнянь регресії та оцінювання міцності їхнього зв’язку. Таке порівняння різних рівнянь регресії можливе на основі певних безрозмірних одиниць вимірювання.

Для лінійної форми зв’язку між результуючою і факторною змінними найчастіше використовують коефіцієнт кореляції r - безрозмірний показник, що характеризує міцність і напрям лінійної залежності між змінними X i Y.

Коефіцієнт кореляції обчислюють т. ч.:

Функція КОРРЕЛ(масив1;масив2) обчислює оцінку коефіцієнта кореляції випадкових величин X i Y.

Коефіцієнт кореляції – використовується для оцінки ступеня лінійної залежності між двома змінними X та Y. Може приймати значення від -1 до +1. При додатних значеннях коефіцієнта кореляції із зростанням факторної змінної x збільшується середнє значення результуючої змінної y; при від’ємних – із зростанням факторної змінної x середнє значення результуючої змінної зменшується y.

Знак коефіцієнта кореляції збігається із знаком коефіцієнта регресії .

Якщо значення коефіцієнта кореляції дорівнює за модулем одиниці, то це означає, що між результуючою і факторною змінними існує функціональний зв'язок. Чим ближче до одиниці, тим сильніший лінійний зв’язок між змінними x і y.

Якщо коефіцієнт кореляції близький до нуля ( ), то зв'язок між змінними x та y відсутній (говорять, що випадкові величини x та y некорельовані, але це не означає, що вони незалежні).

В економічних дослідженнях при значеннях коефіцієнта кореляції 0,7-0,9 зв'язок вважають міцним (сильним), 0,9-0,99 – дуже міцним.

Якщо , то немає змісту шукати пряму, яка найкращим чином описує експериментальні дані.

Така оцінка є експертною і наближеною. Для точнішої оцінки міцності зв’язку необхідно ще враховувати зміст і мету дослідження, обсяг початкових спостережень тощо.

Приклади, як можуть виглядати різні кореляції щодо міцності і напрямку взаємозв’язку.

r=+0,85	r=-0,52
r=+1	r=-1

Діаграми розсіювання з різними кореляціями

Властивості коефіцієнта кореляції:

Кореляція не має одиниць вимірювання. Це означає, що якщо поміняти одиниці вимірювання x та y, то кореляція не зміниться.

Значення x та y в наборі даних можна поміняти місцями, кореляція при цьому не зміниться.

Для нашого прикладу:

Значення коефіцієнта кореляції свідчить про те, що зв'язок між доходом і чистим прибутком фірми є досить міцним.

Оскільки коефіцієнт кореляції високий ( ), то пряма лінія найкращим чином підходить експериментальним даним.

Оскільки між x та y спостерігається кореляція, то між ними існує лінійна залежність. Це означає, що таку залежність можна представити у вигляді прямої лінії. Якщо нам відомі b₀, b₁ то ми можемо підставити значення x і спрогнозувати середнє значення y.

Кореляція вимірює строгість лінійної залежності між числовими змінними.

Якщо між двома змінними існує кореляція, то це не обов’язково означає, що між ними є ще і причинно-наслідковий взаємозв’язок.

Оцінку якості побудованої моделі дає коефіцієнт детермінації R².

Коефіцієнт детермінації дає відповідь на питання, чи справді зміна значення у лінійно залежить саме від зміни значення х, а не відбувається під впливом інших випадкових факторів.

Значення коефіцієнта детермінації набуває значень від 0 до 1 ( .) і характеризує, якою мірою варіація (зміна) залежної змінної y визначається варіацією незалежної змінної x. Чим ближчий він до 1, тим більше варіація залежної змінної визначається варіацією незалежної змінної.

Як правило вважається, якщо , то побудована модель є адекватною реальній дійсності.

Якщо , то залежність між у та x є недостатньою для прийняття моделі. Тоді модель не можна використовувати для економічного аналізу і знаходити значення прогнозу

Для нашого прикладу R²=0,9964. Отже, впливом доходу пояснюється близько 99,64 % варіації прибутку.

Висновок про адекватність лінійного рівняння регресії експериментальним даним робимо на основі критерію Стьюдента.

Обчислимо t-статистику: =40,622

Якщо , то коефіцієнт кореляції генеральної сукупності відмінний від нуля, а кореляційний зв'язок є значним з надійністю 0,95.

Якщо , то модель підібрана невдало, так як вона не узгоджується з експериментальними даними

Отже, вплив доходу на прибуток є значним.

За критерієм Стьюдента і надійністю Р=0,95 модель можна вважати адекватною експериментальним даним (якісною). Коефіцієнт детермінації статистично значимий і включені у регресію фактори достатньо пояснюють стохастичну залежність показника.

Зауваження. Дана формула застосовується, для вибірки, коли n<50.

Якщо n>100, використовується формула: . Величина t має розподіл близький до розподілу Стьюдента (t-розподілу).

Висновки.

Економетрична модель кількісно описує зв'язок чистого прибутку і доходу фірми.

Коефіцієнт b₀=-0,233 економічного змісту не має.

Коефіцієнт регресії b₁=0,831 показує, що при збільшенні доходу фірми на 1 тис. грн. середнє значення чистого прибутку фірми буде збільшуватися на 0,831 тис. грн., тобто на 831 грн.

Коефіцієнт еластичності чистого прибутку залежно від доходу фірми:

EY / X=b₁: = 0,831: =0,7

Отже, із збільшенням доходу фірми на 1 % чистий прибуток зростає на 0,7 %.

Коефіцієнт кореляції R=0,9982 свідчить про досить тісний зв’язок між прибутком та основними фондами.

Значення коефіцієнта детермінації R²=0,9964 показує, що зміна (коливання) значення чистого прибутку фірми на 99,64 % залежить від зміни (коливання) значення доходу і на 0,36 % залежить від зміни значень інших факторів, які в цій регресійній моделі не розглядалися.

З надійністю P=0,95 можна вважати, що отримана модель адекватна до експериментальних даних і на підставі прийнятої моделі проводити економічний аналіз і знаходити значення прогнозу.

Оптимальна пряма для прогнозування прибутку від доходу

Завдання Спрогнозувати прибуток, якщо дохід x=2000.

Ми можемо припустити, що очікуваний (прогнозований) прибуток при доході x=2000 за даною моделлю становить

Моделювання діяльності підприємств у пакеті MS Excel

Побудова моделі парної лінійної регресії в MS Excel

В електронних таблицях MS Excel є декілька способів побудови регресійної моделі:

1. Спосіб: Побудова ГРАФІКА емпіричної і теоретичної лінії регресії (за допомогою майстра діаграм ).

2. Спосіб: Застосування функції ЛИНЕЙН (LINEST);

3. Спосіб: Виконання вбудованого модуля REGRESSION (СервисАнализ данных).

За допомогою цих способів у табличному процесорі MS Excel розраховують:

• оцінки параметрів моделі лінійної регресії, тобто вільний член рівняння і коефіцієнти рівняння регресії;

• оцінка моделі та адекватність до початкових даних за критерієм Фішера;

• значення парних і множинних коефіцієнтів кореляції і детермінації;

• оцінки коефіцієнтів рівняння на статистичну вірогідність за критерієм Стьюдента;

• довірчі інтервали для коефіцієнтів рівняння регресії з ймовірністю p=0,95 і ймовірністю, заданою користувачем;

• результати дисперсійного аналізу (суми квадратів відхилень теоретичних та емпіричних значень результуючої (залежної) ознаки від середнього значення показника, середні значення цих сум).

Статистична функція ЛИНЕЙН ( StatisticalLINEST)

Застосовуючи МНК, дана функція розраховує коефіцієнти лінійної регресії, яка найкращим чином апроксимує дані, а також може обчислити деякі статистичні характеристики цих коефіцієнтів і всього рівняння в цілому.

Синтаксис функції:

=ЛИНЕЙН(значения_Y; значения_X; константа; статистика).

Аргумент константа – логічне значення, яке вказує, чи повинен коефіцієнт b₀ бути рівним 0.

Якщо даний аргумент пропущений, чи має логічне значення ИСТИНА чи будь-яке ненульове числове значення, то коефіцієнт b₀ обчислюється як звичайно.

Якщо аргумент має логічне значення ЛОЖЬ чи 0, то b₀ приймається рівним нулю.

Аргумент статистика приймає логічне значення, яке вказує, чи потрібно розрахувати додаткові статистичні характеристики регресії.

Якщо цей аргумент – логічне значення ИСТИНА чи будь – яке ненульове числове значення, то функція розраховує і виводить ці додаткові характеристики.

Якщо аргумент статистика має логічне значення ЛОЖЬ, 0 чи пропущений, то функція повертає лише значення коефіцієнтів .

Виконання вбудованого модуля регресійного аналізу