Вступ

Економетрія – це напрямок економічної науки, що утворився від поєднання теоретичної економіки, математики та статистики.

Економетрія – це сукупність економічних досліджень, що здійснюються з використанням математичних методів.

Слово “економетрія” означає вимірювання в економіці.

Об’єктом економетрії є економічні системи різного рівня складності: від окремого підприємства чи фірми до економіки галузей, регіонів, держави, світу.

Предмет економетрії – це методи побудови та дослідження математико-статистичних моделей економіки, проведення кількісних досліджень економічних явищ, прогнозування розвитку економічних процесів.

Предметом економетричного дослідження діяльності підприємств є прикладні стохастичні економічні моделі, тобто економічні моделі, в яких параметри набувають конкретних числових значень залежно від використовуваної статистичної інформації.

Метою економетричного дослідження є аналіз економічних систем і процесів, що в них відбуваються, за допомогою економетричних методів і моделей, їх застосування при прийнятті управлінських рішень.

Основне завдання економетрії – оцінити параметри моделей з урахуванням особливостей вхідної економічної інформації, перевірити відповідність моделей досліджуваному явищу і спрогнозувати розвиток економічних процесів.

Основні етапи економетричного аналізу:

1. вибір конкретної форми аналітичної залежності між економічними показниками (специфікація моделі);

2. збір та підготовка статистичної інформації;

3. оцінка параметрів моделі;

4. перевірка адекватності моделі та достовірності її параметрів за допомогою відповідних статистичних критеріїв;

5. застосування моделі для прогнозування розвитку економічних процесів з метою подальшого керування ними.

Ми будемо розглядати економетричне моделювання діяльності підприємств, тобто будемо аналізувати діяльність підприємств за допомогою економетричних моделей.

Тема 1. Побудова простої однофакторної економетричної моделі

1. Поняття простої економетричної моделі та етапи її побудови.

2. Оцінка параметрів економетричної моделі методом найменших квадратів (1 МНК).

3. Оцінка достовірності моделі

Поняття простої економетричної моделі та етапи її побудови.

Означення

Економетрія – це розділ економічної науки, в якому вивчаються методи кількісного вимірювання взаємозв’язків між економічними показниками.

Економетрична модель – це математична функція (вираз), яка найкращим чином описує реально існуючі взаємозв’язки між економічними показниками.

Загальний вигляд економетричної моделі:

Y =f(X,e)

де X – вхідні економічні показники (незалежні (екзогенні) змінні, фактори), Y –  залежна (ендогенна) змінна (результативна ознака) e – випадкова або стохастична складова (похибка), що виявляє відхилення реальних даних від теоретичної моделі регресії (залишки моделі, що містять ту частину зміни Y, яка не пояснюється впливом факторних ознак x_1, x_{2, …} x_n і має випадковий характер).

Складова e – випадкова змінна, а оскільки залежна змінна Y залежить від e, вона теж стохастична.

Аналітична форма цієї моделі може бути різною. Найпоширенішими є такі форми моделей:

де b₀, b₁ – невідомі параметри моделі, e – стохастична (статистична, випадкова) складова, - фактичне значення результуючої ознаки.

Оцінка параметрів економетричної моделі методом найменших квадратів

Нехай при дослідженні деякого економічного явища отримаємо n значень (x_i,y_i). Результати спостережень записані у вигляді таблиці:

Таблиця 1

x	x1	x2	…	xi	…	xn
y	y1	y2	…	yi	…	yn

де y_i, x_i – фактичні значення і-го спостереження, i – номер спостереження, n –  кількість усіх спостережень.

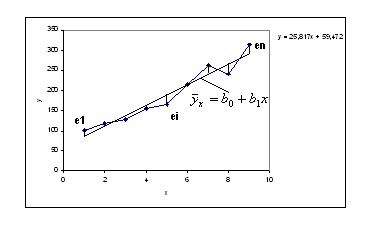
За цими даними необхідно визначити вигляд функціональної залежності між x та y, тобто від табличної форми представлення функціональної залежності необхідно перейти до аналітичної форми її представлення, виду Y =f(X,e) або M(Y/X)= ₀+₁x.

Для визначення функціональної залежності:

1. зображаємо графічно точки (x_i,y_i) i=1…n;

2. по характеру розташування точок вибираємо форму залежності між x та y (лінійну, параболічну, гіперболічну, показникову). На цьому етапі параметри b₀, b₁ – невідомі.

Нам потрібно знайти пряму, яка б найкраще відображала закономірність зв’язку середнього значення результуючої змінної з факторною – пряма регресії повинна розташовуватися якнайближче до всіх точок із координатами (x_i, y_i).

Припустимо, що точки (x_i, y_i) i=1…n, на кореляційному полі групуються навколо прямої лінії. .

Розглядаємо лінійну економетричну модель, де стохастична складова e має нульове математичне сподівання і постійну дисперсію.

(1)

Сполучаючи отримані точки (x_i,y_i) i=1…n відрізками прямої, отримуємо ламану лінію – лінію емпіричної регресії. Похибкою емпіричної регресії є стрибкоподібність (нерівномірність) зміни результуючої ознаки при збільшенні факторної змінної, що не відображає реальної залежності Y від X.

Емпірична лінія регресії відображає не лише основну закономірність, але і різні відхилення від неї. Це обумовлює доцільність побудови не ламаної лінії регресії, а прямої чи неперервної кривої, яка б відображала загальну закономірність зв’язків, не залежних від випадкових впливів. Таку пряму (криву) лінію називають лінією теоретичної регресії, а рівняння, яке її описує – рівнянням регресії (кореляційне рівняння чи рівняння зв’язку).

Регресія – це залежність середнього значення певної величини від деякої іншої величини або кількох величин. Залежність між економічними показниками часто описують лінійним рівнянням регресії.

Завдання полягає в знаходженні невідомих параметрів _0,, ₁. Але справжні значення одержати неможливо, оскільки ми спираємось на обмежену вибірку. Тому знайдені значення параметрів b₀, b₁ будуть статистичними оцінками справжніх (невідомих нам) параметрів. Отже, рівняння парної регресії: , де характеризує деяке середнє значення для даного значення .

Залежність між двома змінними може бути функціональною або статистичною.

При функціональній залежності кожному значенню незалежної змінної відповідає єдине строго визначене значення залежної змінної. Як показує досвід, функціональні співвідношення між соціально – економічними показниками (за винятком тих випадків, коли вони встановлюються за означенням) практично не існують. Для соціально – економічної сфери характерні такі зв’язки, коли кожному значенню випадкової незалежної змінної (ознаки) відповідає певна множина результуючої ознаки. Такі зв’язки називаються стохастичними (статистичні, випадкові), вони можуть мати різний характер. Ми будемо розглядати лише кореляційний зв'язок.

3. для оцінки параметрів модельного рівняння регресії b₀, b₁ застосовують метод найменших квадратів.

Умова методу найменших квадратів для знаходження параметрів b₀ та b₁ має вигляд:

- умова мінімуму суми квадратів відхилень табличних (спостережуваних) даних (точок (x_i,y_i)) від вибраної функціональної залежності (лінії регресії),

де i – номер спостереження, n –  кількість усіх спостережень, - фактичні (експериментальні) дані, - теоретичні (розрахункові) значення

Функція буде мати мінімальне значення, коли відповідні часткові похідні дорівнюють нулю:

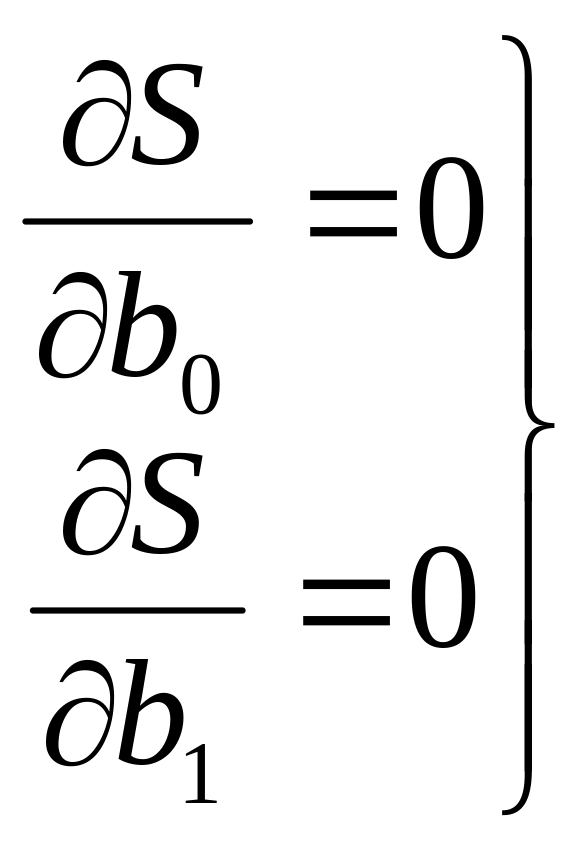(1)

Розв’язуючи систему (1) матричним способом, знаходимо:

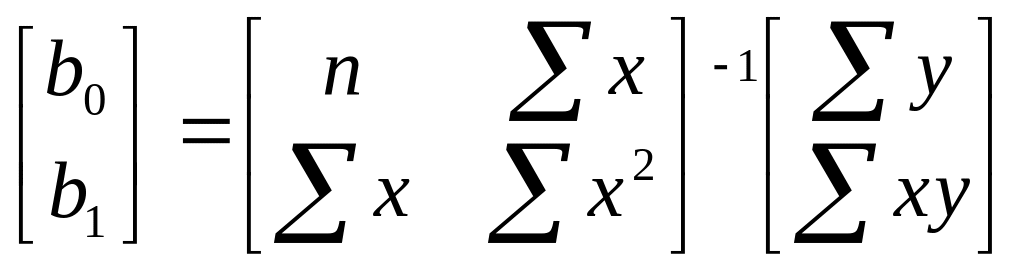, де

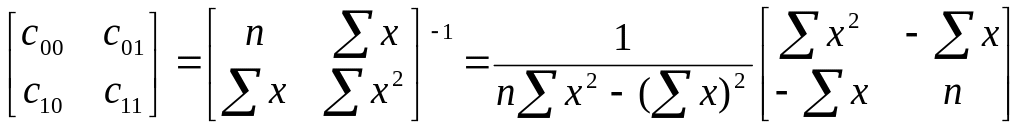С= (2)

(2) – ковариційно – дисперсійна матриця системи нормальних рівнянь (1).

Тоді розв’язком є значення коефіцієнтів b₀ і b₁.

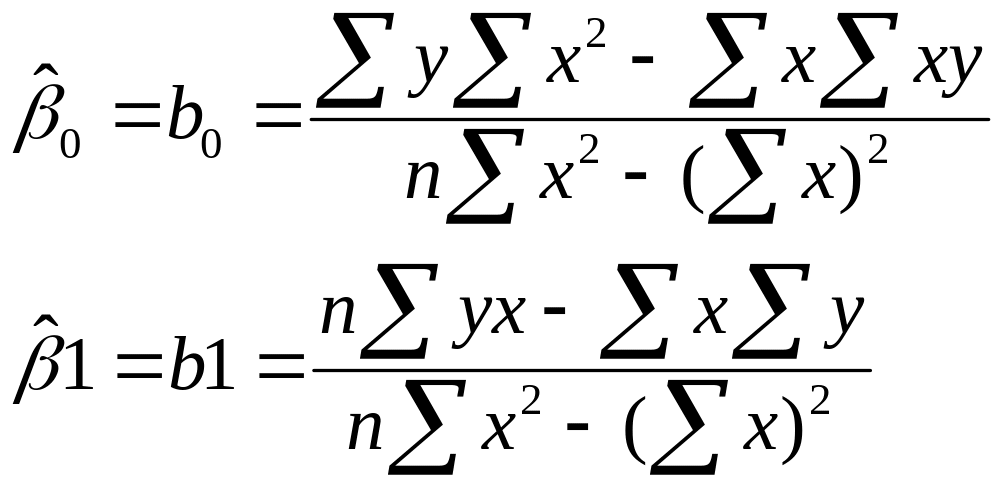
Метод найменших квадратів можна реалізувати за допомогою програми MS Excel.

Точкові оцінки невідомих параметрів модельної лінії регресії не дозволяють безпосередньо дати відповідь на питання, яке відхилення здійснюється, якщо замість точного значення невідомого параметра b приймається його наближене значення.

Щоб охарактеризувати, наскільки оптимально отримана функція регресії відображає залежність між середніми значеннями Y і фіксованими значеннями x, перевіряємо адекватність прийнятої моделі (лінійної функції регресії) експериментальним даним (x_i, y_i) i=1…n.

Оцінка достовірності моделі

На попередньому етапі ми отримали конкретні значення невідомих коефіцієнтів b₀ та b₁. Але ці значення ми отримали для деякої вибірки спостережень. Тому потрібно перевірити, чи ці значення узгоджуються з відповідними коефіцієнтами генеральної сукупності, тобто перевірити їхню статистичну значущість. Для цього використовують t-критерій Стьюдента.

Також на цьому етапі необхідно перевірити статистичну значущість показників, які визначають міцність зв’язку між ендогенною змінною (Y) та екзогенними змінними (X), тобто множинних коефіцієнтів детермінації і кореляції. Статистичну значущість коефіцієнта множинної кореляції перевіряють за допомогою t-критерію Стьюдента, а множинного коефіцієнта детермінації – за допомогою F-критерію Фішера. Якщо коефіцієнт детермінації є статистично значущим, то побудована модель (1) є адекватною експериментальним даним.

Після того, як вибрано модель, і встановлено, що вона є адекватною за F-критерієм, її можна використовувати для прогнозу.

Приклад

За допомогою електронних таблиць MS Excel побудувати лінійну однофакторну модель залежності чистого прибутку (тис. грн.) фірми від доходу (тис. грн.).

Роки	Дохід, тис. грн	Чистий прибуток, тис.грн
2004	2181,3	1835,7
2005	2171,9	1826,6
2006	2128,3	1713,6
2007	1741,5	1451,2
2008	1401,1	1167,6
2009	905,4	745,5
2010	1362,2	1135
2011	1260,2	1050,5

На основі отриманих результатів зробити висновки:

1. ідентифікувати змінні;

2. побудувати точкову діаграму;

3. побудувати графік емпіричної і теоретичної лінії регресії;

4. оцінити параметри моделі, використовуючи метод найменших квадратів;

5. провести перевірку адекватності моделі за допомогою відповідних статистичних критеріїв.

Розв’язок