
- •Учебно-методические указания
- •Учебно-методические указания
- •Самостоятельная работа студентов. Практические занятия. Модуль 1. Дифференциальное исчисление
- •Тема 1.1. Числовые последовательности и функции
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий
- •III.Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 1.2. Предел и непрерывность функции.
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий
- •III.Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •Тема 1.3. Дифференциальное исчисление функции одной переменной
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий
- •III.Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 1.4. Применение дифференциального исчисления для исследования функций и построения графиков
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий
- •III.Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 1.5. Функции нескольких переменных.
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий (3 час.)
- •III. Рекомендации по выполнению заданий
- •§ 1, § 2 Главы 9 учебника [1] , в главе 15 учебника [2]
- •Основная литература
- •Дополнительная литература
- •Тема 1.6. Экстремумы функций двух переменных.
- •Основная литература
- •Дополнительная литература
- •Тема 2.1. Неопределенный интеграл
- •II. Планы практических занятий (4 ч.)
- •III. Рекомендации по выполнению заданий и подготовке
- •Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 2.2. Определенный интеграл
- •1. Задания для самостоятельной работы
- •II. Планы практических занятий (4 ч.)
- •III. Рекомендации по выполнению заданий и подготовке
- •§ 11.6 Учебника [1] и главе 7, § 7.4-7.6 задачника [2]
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 3.1. Дифференциальные уравнения первого порядка
- •1. Задания для самостоятельной работы
- •II. Планы практических занятий (3 час.)
- •III. Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 3.2. Линейные дифференциальные уравнения второго порядка
- •1. Задания для самостоятельной работы
- •II. Планы практических занятий (3 час.)
- •III. Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Тема 3.3. Числовые ряды.
- •I. Задания для самостоятельной работы
- •II. Планы практических занятий (3 час)
- •III. Рекомендации по выполнению заданий и подготовке
- •IV. Рекомендуемая литература Основная литература
- •Дополнительная литература
- •Тема 3.4. Степенные ряды.
- •Основная литература
- •Дополнительная литература
- •V. Контрольные вопросы для самопроверки
- •Примерная тематика контрольных работ
- •Вопросы для подготовки к экзамену
Тема 3.4. Степенные ряды.
I. Задания для самостоятельной работы
1. Изучить теоретический материал по вопросам:
1.1. Понятие степенного ряда. Интервал сходимости степенного ряда.
1.2. Теорема Абеля. Нахождение радиуса сходимости.
1.3. Свойства степенных рядов.
1.4. Понятие о рядах Тейлора, Маклорена.
2. Выполнить задания:
2.1. № 1-15, стр. 49 из учебного пособия [1].
2.2. № 1-8, стр. 68-69 из учебного пособия [2].
II. Планы практических занятий (3 час)
ТЕМА. Определение области сходимости степенного ряда (2 часа).
1. Область сходимости степенного ряда.
2. Радиус сходимости.
3. Исследование в граничных точках.
ТЕМА. Ряды Тейлора и Маклорена (1 часа)
1. Ряды Тейлора.
2. Ряды Маклорена для элементарных функций. Конкретные разложения.
III. Рекомендации по выполнению заданий и подготовке
к практическому занятию
1. Теоретический материал и примеры решения типовых задач по теме «Область сходимости степенного ряда» изложены в учебном пособии [1] в главе 3.
2. Теоретический материал и примеры решения типовых задач по теме «Ряды Тейлора и Маклорена» изложены в главе 4 учебного пособия [1].
IV. Рекомендуемая литература
Основная литература
1. Виленкин И.В. Числовые и степенные ряды: учебное пособие / И.В. Виленкин , В.М. Гробер . –Ростов н/Д: РИО Ростовского филиала РТА, 2004.
2. Кремер, Н. Ш. Высшая математика для экономистов : учебник / Н. Ш. Кремер, Б. А. Путко, И. М. Фридман. – М.: Банки и биржи, ЮНИТИ, 2007.
3. Ермаков, В. И. Общий курс высшей математики для экономистов: учебник / В. И. Ермаков, Б. М. Рудык. – М.: ИНФРА-М, 2008.
Дополнительная литература
Бугров Я.С., Дифференциальные уравнения. Кратные интегралы. Ряды : учебник /Я.С. Бугров, С.М. Никольский. – М.: Наука, 2006.
V. Контрольные вопросы для самопроверки
1. Какой ряд называют степенным рядом?
2. Что называется радиусом сходимости степенного ряда?
3. Как определяется радиус сходимости степенного ряда?
4. Какие ряды называют рядами Тейлора и Маклорена?
5. Какой вид имеют ряды Маклорена для функций у = ех, y = sinx, y = cosx,
y = (1 + x)m ?
Примерная тематика контрольных работ
Первый семестр
Вычисление пределов и производных.
Исследование функций.
Вычисление неопределённых и определенных интегралов.
4. Функции многих переменных: частные производные, экстремумы.
5. Дифференциальные уравнения первого порядка. Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами.
6. Числовые и степенные ряды.
Темы курсовых работ по математическому анализу
Гиперболические функции.
Исследование функций
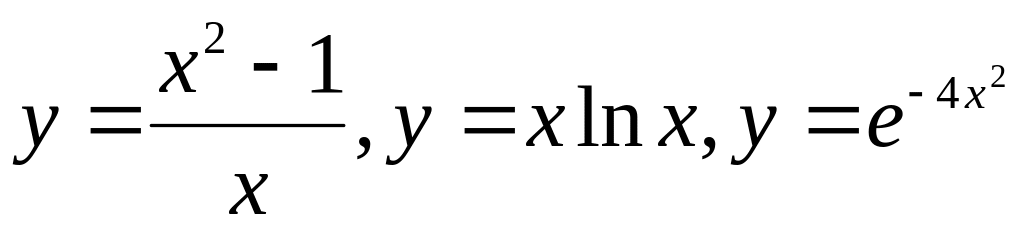 и построение их графиков.
и построение их графиков.Исследование функций
 и построение их графиков.
и построение их графиков.Исследование функций
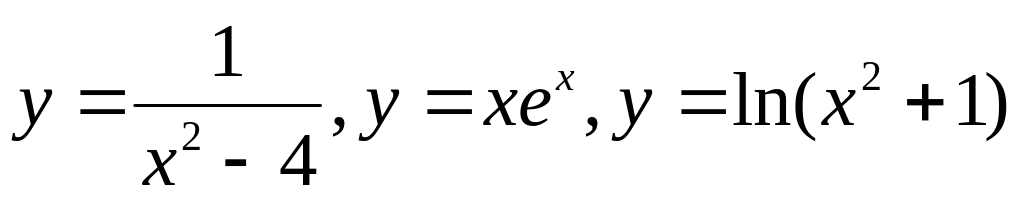 и построение их графиков.
и построение их графиков.Исследование функций
 и построение их графиков.
и построение их графиков.Исследование функций
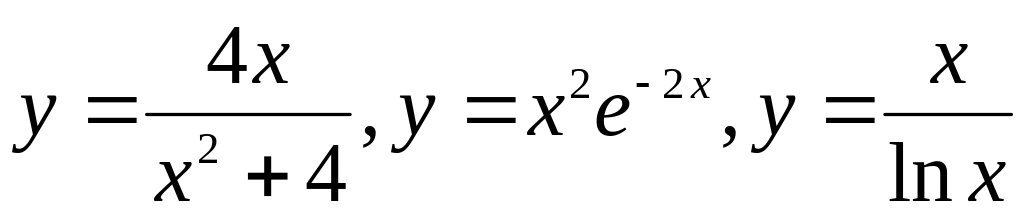 и построение их графиков.
и построение их графиков.Исследование функций
 и построение их графиков.
и построение их графиков.Исследование функций
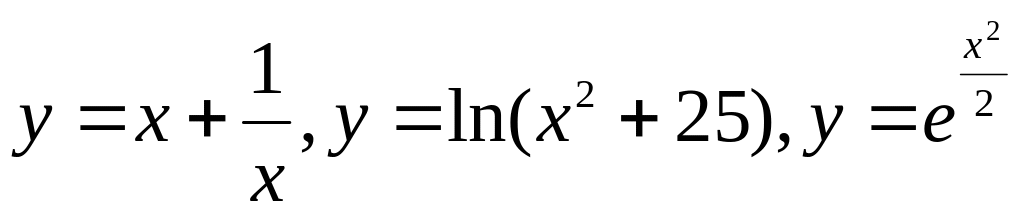 и построение их графиков.
и построение их графиков.Исследование функций

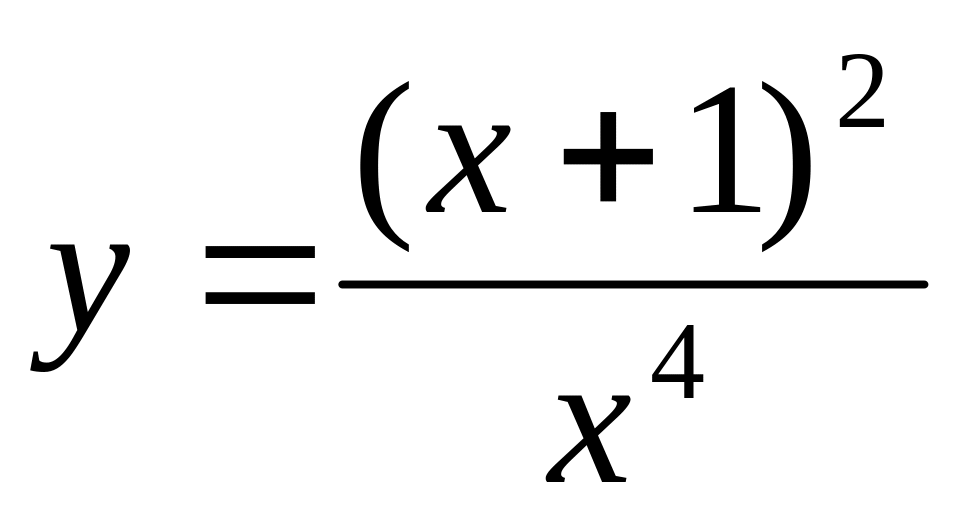 и построение их графиков.
и построение их графиков.Исследование функций
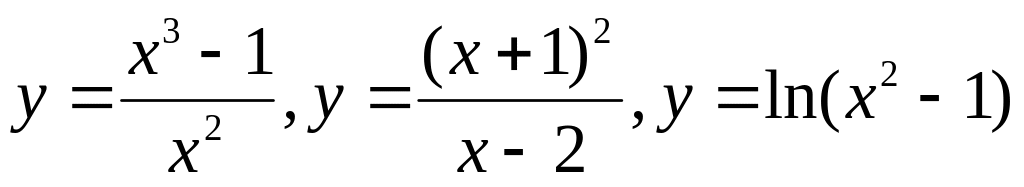 и построение их графиков.
и построение их графиков.Исследование функций
 и построение их графиков.
и построение их графиков.Исследование функций
 и построение их графиков.
и построение их графиков.Исследование функций
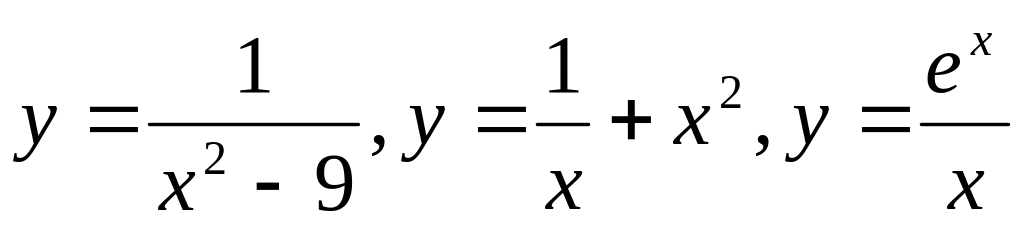 и построение их графиков.
и построение их графиков.Исследование функций
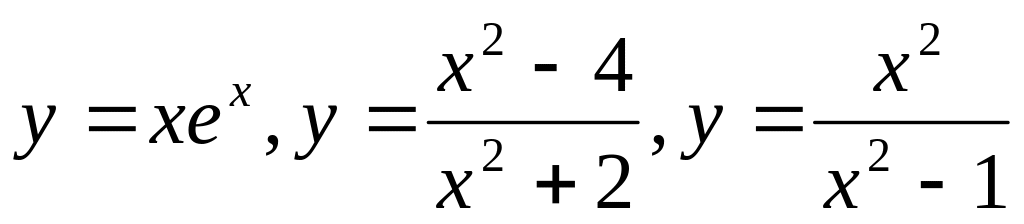 и построение их графиков.
и построение их графиков.Эластичность функций одной и нескольких переменных.
Условный экстремум, метод множителей Лагранжа.
Частные производные и дифференциалы высших порядков.
Интегрирование рациональных дробей.
Интегрирование некоторых иррациональных выражений.
Двойной интеграл и его приложения.
Приближенные методы вычисления определенного интеграла.
Несобственные интегралы.
Разложение функций
 в степенной ряд. Приближенные вычисления
с помощью этих рядов.
в степенной ряд. Приближенные вычисления
с помощью этих рядов.Разложение функций
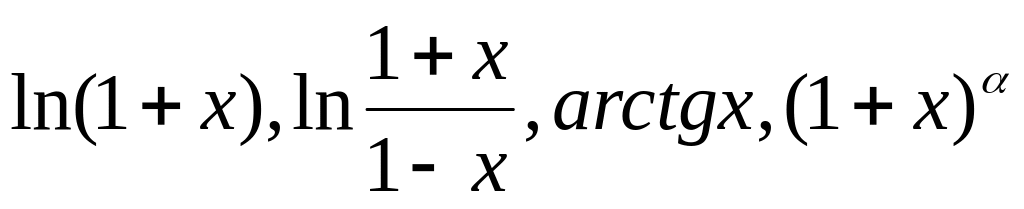 в степенной ряд. Приближенные вычисления
с помощью этих рядов.
в степенной ряд. Приближенные вычисления
с помощью этих рядов.Линейные дифференциальные уравнения с постоянными коэффициентами.
Приложения определенного интеграла.
Функции многих переменных, их дифференцирование.
Интегрирование тригонометрических функций.
Задача потребительского выбора.
Производственные функции.
