4.2Коллизия

Коллизия - это когда на входе хеш-функции разные тексты (строки), а на выходе - одинаковые хеш-значения.

Коллизии дают возможность некоторых махинаций с электронными документами. Допустим, документы контролируются по хешам. Тогда можно составить два документа с одинаковым хешем и в нужный момент сделать подмену. Вышеприведенный пример Штирлица подвержен коллизии первого рода, в силу того, что по знанию количеству букв «а= », «б= », «в= », … , «я= » можно составить другой документ на 10 страниц, но по этим буквам, практически невозможно восстановит оригинал документа.

Другой пример, когда коллизии могут навредить, - это применение хеш-функций для контроля целостности файлов, сетевых сообщений и т.п. Файл (сообщение) проверяется на наличие искажения с помощью хеш-функции. Если у него новый хеш - искажение было. Если хеш тот же, то может быть, что искажение было, но вышло так, что хеш-функция дала для обеих версий одинаковое значение.

Разрешение коллизий

Это специальный алгоритм, который используется каждый раз при размещении новой записи или при поиске существующей, если возникла коллизия.

В системах БД рехеширование выполняется одним из следующих способов:

1. Открытая адресация: новая запись размещается вслед за последней записью на данной странице или на следующей, если страница заполнена.

2. Использование коллизионных страниц: новая запись размещается на одной из коллизионных страниц, относящихся к таблице (в области переполнения). Для ускорения поиска рехешированных записей может использоваться связанная область переполнения, для которой на странице хранится ссылка на коллизионную страницу. Нулевое значение такой ссылки говорит об отсутствии коллизий для данных, размещённых на этой странице.

3. Многократное хеширование. Заключается в том, что при возникновении коллизии для поиска другого адреса (возможно, на коллизионных страницах) применяется другая функция хеширования.

Сильная устойчивость к коллизиям (1-го рода): для нарушителя

вычислительно неосуществимо найти x' такое, чтобы x и x' образовали коллизию (т. е.

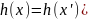, в т.ч. при данных и

Слабая устойчивость к коллизиям (2-го рода): для нарушителя

вычислительно неосуществимо построить второй вход x' такой, ч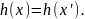то Это

подразумевает, что при данном неосуществимо найти любой x', такой что

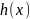
(т. е. h является однонаправленной функцией).

4.4Пример простого хеширования

Для легкого усвоения материала данного раздела мы приведем достаточно простой пример хеш-функции на маленьких числах. Скажем, используя данные задачи необходимо получить хеш-код 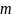для некоторого сообщения 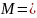«ИНТЕГРАЛ» при помощи хеш-функции H. Выберем вектор инициализации 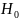равным нулю.

Хеш-функцию можно записать следующим образом:

,

где ;

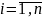Н₀ – вектор инициализации;

М_i=М₁, М₂, … , М_n – длина блока.

Все блоки делят пополам и к каждой половине прибавляют равноценное количество единиц. С образованными таким образом блоками производят итерационные действия.

Нам необходимо получить хеш-значение сообщения ИНТЕГРАЛ при помощи хеш-функции с параметрами 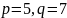. «И–10=1010₂», «Н–15=1111₂», «Т–20=10100₂»…, «Л–13=1101₂» порядковый номер буквы в алфавите.

Вычислим хеш-код:

00001010:00001111:00010100:00000110:00000100:00010010:00000001:00001101

1. рассчитаем значение модуля n = p*q = 35;

2. представим сообщение в виде номеров букв русского алфавита в десятичном и двоичном видах (байтах):

И	Н	Т	Е	Г	Р	А	Л
10	15	20	6	4	18	1	13
0000:1010	0000:1111	0001:0100	0000:0110	0000:0100	0001:0010	0000:0001	0000:1101

3. разобьем байты пополам, добавив в начало полубайт равный 0100 и получим хешируемые блоки М_i:

M1	M2	M3	M4	M5	M6	M7	M8
0100:0000	0100:1010	0100:0000	0100:1111	0100:0001	0100:0100	0100:0000	0100:0110
M9	M10	M11	M12	M13	M14	M15	M16
0100:0000	0100:0100	0100:0001	0100:0010	0100:0000	0100:0001	0100:0000	0100:1101

4. выполним итеративные шаги:

первая итерация

М₁ = 01000000

Н₀ = 00000000

Н₀ М₁ = 01000000 = 64₁₀

[(H₀ M₁)²] (mod 35) = 64²(mod 35) = 1₁₀

H₁ = 1₁₀ = 00000001₂

вторая итерация

М₂ = 01001010

Н₁ = 00000001

Н₁ М₂ = 01001011 = 75₁₀

[(H₁ M₂)²] (mod 35) = 75²(mod 35) = 25₁₀

H₂ = 25₁₀ = 00011001₂

третья итерация

М₃ = 01000000

Н₂ = 00011001

Н₂ М₃ = 01011001 = 89₁₀

[(H₂ M₃)²] (mod 35) = 89²(mod 35) = 11₁₀

H₃ = 11₁₀ = 00001011₂

четвертая итерация

М₄ = 01001111

Н₃ = 00001011

Н₃ М₄ = 01000100 = 68₁₀

[(H₃ M₄)²] (mod 35) = 68²(mod 35) = 4₁₀

H₄ = 4₁₀ = 00000100₂

пятая итерация

М₅ = 01000001

Н₄ = 00000100

Н₄ М₅ = 01000101 = 69₁₀

[(H₄ M₅)²] (mod 35) = 69²(mod 35) = 1₁₀

H₅ = 1₁₀ = 00000001₂

шестая итерация

М₆ = 01000100

Н₅ = 00000001

Н₅ М₆ = 01000101 = 69₁₀

[(H₅ M₆)²] (mod 35) = 69²(mod 35) = 1₁₀

H₆ = 1₁₀ = 00000001₂

седьмая итерация

М₇ = 01000000

Н₆ = 00000001

Н₆ М₇ = 01000001 = 65₁₀

[(H₆ M₇)²] (mod 35) = 65²(mod 35) = 25₁₀

H₇ = 25₁₀ = 00011001₂

восьмая итерация

М₈ = 01000110

Н₇ = 00011001

Н₇ М₈ = 01011111 = 95₁₀

[(H₇ M₈)²] (mod 35) = 95²(mod 35) = 30₁₀

H₈ = 30₁₀ = 00011110₂

девятая итерация

М₉ = 01000000

Н₈ = 00011110

Н₈ М₉ = 01011110 = 94₁₀

[(H₈ M₉)²] (mod 35) = 94²(mod 35) = 16₁₀

H₉ = 16₁₀ = 00010000₂

десятая итерация

М₁₀ = 01000100

Н₉ = 00010000

Н₉ М₁₀ = 01010100 = 84₁₀

[(H₉ M₁₀)²] (mod 35) = 84²(mod 35) = 21₁₀

H₁₀ = 21₁₀ = 00010101₂

одиннадцатая итерация

М₁₁ = 01000001

Н₁₀ = 00010101

Н₁₀ М₁₁ = 01010100 = 84₁₀

[(H₁₀ M₁₁)²] (mod 35) = 84²(mod 35) = 21₁₀

H₁₁ = 21₁₀ = 00010101₂

двенадцатая итерация

М₁₂ = 01000010

Н₁₁ = 00010101

Н₁₁ М₁₂ = 01010111 = 87₁₀

[(H₁₁ M₁₂)²] (mod 35) = 87²(mod 35) = 9₁₀

H₁₂ = 9₁₀ = 00001001₂

тринадцатая итерация

М₁₃ = 01000000

Н₁₂ = 00001001

Н₁₂ М₁₃ = 01001001 = 73₁₀

[(H₁₂ M₁₃)²] (mod 35) = 73²(mod 35) = 9₁₀

H₁₃ = 9₁₀ = 00001001₂

четырнадцатая итерация

М₁₄ = 01000001

Н₁₃ = 00001001

Н₁₃ М₁₄ = 01001000 = 72₁₀

[(H₁₃ M₁₄)²] (mod 35) = 72²(mod 35) = 4₁₀

H₁₄ = 4₁₀ = 00000100₂

пятнадцатая итерация

М₁₅ = 01000000

Н₁₄ = 00000100

Н₁₄ М₁₅ = 01000100 = 68₁₀

[(H₁₄ M₁₅)²] (mod 35) = 68²(mod 35) = 4₁₀

H₁₅ = 4₁₀ = 00000100₂

шестнадцатая итерация

М₁₆ = 01001101

Н₁₅ = 00000100

Н₁₅ М₁₆ = 01001001 = 73₁₀

[(H₁₅ M₁₆)²] (mod 35) = 73²(mod 35) = 9₁₀

H₁₆ = 9₁₀ = 00001001₂

Таким образом, исходное сообщение «интеграл» имеет хеш-код m = 9.

Для вычисления цифровой подписи используем следующую формулу:

= 9⁵ mod (35) = 4.

Пара (M, S) передается получателю как электронный документ М, подписанный цифровой подписью S, причем подпись S сформирована обладателем секретного ключа d.

Получив пару (M, S), получатель вычисляет хеш-код сообщения М двумя способами:

1. восстанавливает хеш-код m^/, применяя криптографическое преобразование S с использованием открытого ключа e:

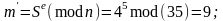
2. находит результат хеширования принятого сообщения с помощью той же хеш-функции:

m = H(M) = 9.

При равенстве вычисленных значений m и m^/ получатель признает пару (M, S) подлинной, т.е. сообщение – оригинальным.