
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ХАРКІВСЬКИЙ НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ РАДІОЕЛЕКТРОНІКИ
Лекція 5 Тема: " Розфарбування графів. Хроматичне число. Хроматичний клас " Дисципліна : "Дискретна математика"
Викладач: Гусарова І. Г.
Харків 2014
ЗМІСТ
Хроматичне число……………………………………………………..3
Хроматичний клас……………………………………………………..5
Число внутрішньої стійкості…………………………………………6
Запитання для перевірки…………………………………………......9
1.Хроматичне число
Розфарбуємо
кожну вершину (відповідно, кожне ребро)
графа
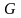 в який-небудь
колір.
в який-небудь
колір.
Визначення. Розфарбування вершин (ребер) графа називається правильним, якщо ніякі дві суміжні вершини (два суміжних ребра) не пофарбовані в той самий колір.
Означення.
Граф
називається
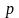 -хроматичним,
якщо він допускає правильне вершинне
фарбування у
фарб.
-хроматичним,
якщо він допускає правильне вершинне
фарбування у
фарб.
Правильне розфарбування вершин звичайно називають просто розфарбуванням графа.
Визначення.
Найменше число кольорів
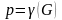 ,
якими можна розфарбувати граф, називається
хроматичним
числом
цього графа.
,
якими можна розфарбувати граф, називається
хроматичним
числом
цього графа.
Наприклад, граф, показаний на малюнку 5.1, є 5-хроматичним,
4- хроматичним, 3-хроматичним.
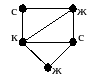
Рис. 5.1
Його хроматичне число 3.
Теорема 1 (Кеніг). Для того, щоб граф був біхроматичним, необхідно й досить, щоб він не мав циклів непарної довжини.
Достатність.
Нехай
– граф без циклів непарної довжини,
 – довільна його вершина. Пофарбуємо її
в червоний колір. Всі суміжні з нею
вершини пофарбуємо в сині кольори. Всі
вершини, суміжні з пофарбованими синім,
пофарбуємо в червоні кольори й т.д. при
цьому ніяка вершина
– довільна його вершина. Пофарбуємо її
в червоний колір. Всі суміжні з нею
вершини пофарбуємо в сині кольори. Всі
вершини, суміжні з пофарбованими синім,
пофарбуємо в червоні кольори й т.д. при
цьому ніяка вершина
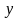 не може виявитися й червоної, і синьої,
тому що це означало б, що існує два
ланцюги, що з'єднують
й
,
з яких один – парної довжини, а інший –
непарної (якщо об'єднаємо їх у цикл, то
одержимо цикл непарної довжини,
протиріччя).
не може виявитися й червоної, і синьої,
тому що це означало б, що існує два
ланцюги, що з'єднують
й
,
з яких один – парної довжини, а інший –
непарної (якщо об'єднаємо їх у цикл, то
одержимо цикл непарної довжини,
протиріччя).
Необхідність.
Нехай
– біхроматичний граф. Розфарбуємо його
вершини в червоний і синій кольори так,
щоб ніякі дві суміжні вершини не були
пофарбовані в один кольори. Нехай
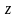 – деякий цикл графа
.
При його обході червоні й сині вершини
будуть чергуватися. Отже, загальне число
вершин циклу, а значить і ребер, парно.
– деякий цикл графа
.
При його обході червоні й сині вершини
будуть чергуватися. Отже, загальне число
вершин циклу, а значить і ребер, парно.
Нижче приведемо один зі способів знаходження хроматичного числа.
1.
Довільним образом правильно розфарбуємо
граф
кольорами
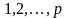 .
.
2.
Вибираємо деякий колір
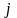 в якості «критичного» і намагаємося
виключити його. Нехай
– деяка вершина кольору
,
в якості «критичного» і намагаємося
виключити його. Нехай
– деяка вершина кольору
,
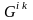 – підграф графа
,
породжений вершинами кольорів
– підграф графа
,
породжений вершинами кольорів
 ,
відмінних від
,
,
відмінних від
,
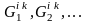 – компоненти зв’язности
графа
;
– компоненти зв’язности
графа
;
 – множина всіх суміжних з
вершин у компоненті
– множина всіх суміжних з
вершин у компоненті
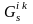 .
Якщо не всі множини
однокольорові, то якщо буде потреба
поміняємо в
між собою кольори
так, щоб всі
були пофарбовані в один колір, наприклад
.
Якщо не всі множини
однокольорові, то якщо буде потреба
поміняємо в
між собою кольори
так, щоб всі
були пофарбовані в один колір, наприклад
 .
Після цього вершину
перефарбуємо в колір
.
Після цього вершину
перефарбуємо в колір
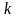 .
Розфарбування вершин графа при цьому
залишається правильним.
.
Розфарбування вершин графа при цьому
залишається правильним.
3. Якщо залишилися вершини, що мають обраний раніше критичний колір, то повторюємо крок 2 для цього кольору. Якщо ні, то вибираємо в якості критичного інші кольори. Повторюємо крок 2 доти, поки це можливо.
Приклад. На мал. 5.2 наведений граф, пофарбований в 4 кольори (їм відповідають цифри 1,2,3,4).
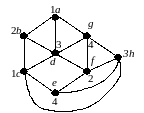
Рис. 5.2
Виберемо
в якості критичного кольору колір 1. Їм
пофарбовані вершини
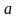 й
й
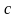 .
Розглянемо компоненти зв’язності
.
Розглянемо компоненти зв’язності
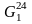 й
й
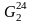 .
Перша з них породжена вершинами
.
Перша з них породжена вершинами
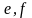 й
й
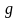 ,
друга вершиною
,
друга вершиною
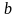 .
У кожній компоненті тільки одна вершина
суміжна з вершиною
,
.
У кожній компоненті тільки одна вершина
суміжна з вершиною
,
 .
Міняємо в компоненті
кольори 2 й 4 між собою. У результаті
одержимо розфарбування, показане на
мал. 5.3.
.
Міняємо в компоненті
кольори 2 й 4 між собою. У результаті
одержимо розфарбування, показане на
мал. 5.3.
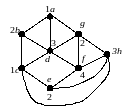
Рис. 5.3
Тепер вершини й пофарбовані в колір 4 (мал. 5.4).
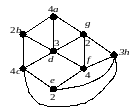
Рис. 5.4
Граф виявляється пофарбованим в 3 кольори. Тому що він містить цикли непарної довжини, то меншим числом фарб його розфарбувати не можна. Отже, його хроматичне число 3.
Помітимо, що описаний вище спосіб не завжди приводить до відшукання хроматичного числа графа. У книзі Крістофідеса “Теорія графів” наведені й інші способи знаходження хроматичного числа графа, у тому числі й позбавлені зазначеного недоліку - вони завжди приводять до шуканого результату.
