3.2. Момент силы относительно точки и оси
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис.3.3).
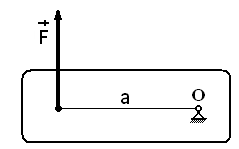
Рис.3.3
При закреплении тела в точке О сила F стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а называется плечом силы относительно центра момента. Момент силы F относительно точки О определяется произведением силы на плечо
М0 = F·a.
Измеряют моменты сил в ньютон-метрах (Н м) или в соответствующих кратных и дольных единицах, как и моменты пар.
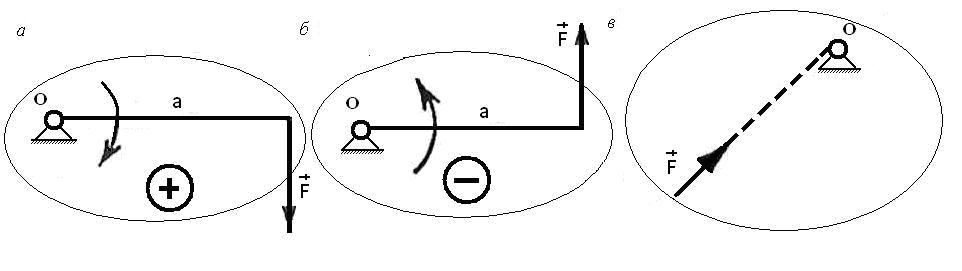
Рис. 3.4
Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке (рис. 3.4, а), а отрицательным - против часовой стрелки (рис. 3.4, б). Когда линия действия силы проходит через данную точку, момент силы относительно этой точки равен нулю, так как в рассматриваемом случае плечо а = 0 (рис. 3.4, в).
Для определения момента силы относительно оси нужно спроецировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью (рис. 31).
МОО (F) = пр F а ,(рис. 3.5)
где а — расстояние от оси до проекции F;
пр F — проекция силы на плоскость, перпендикулярную оси 00;
пр F = F cos a; Mоo (F) = F cos α a.
.
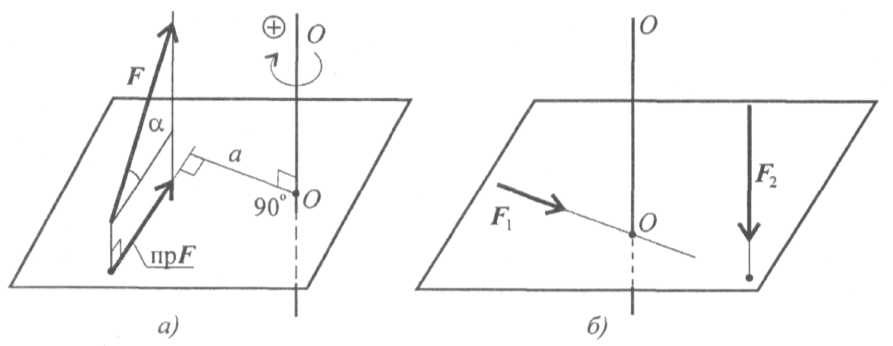
Рис. 3.5
3.3. Приведение произвольной системы сил к заданному центру
Приведем систему трех произвольно расположенных сил F1, F2 и F3, приложенных к твердому телу в точках А1, А2 и А3, к заданному центру О.
Получим три силы F1'', F2" и F3'', приложенные в центре О, и три присоединенные пары сил F1, F1', F2, F2'и F3, F '3 (рис.3.6). Складывая силы F1'', F2" и F3'' по правилу многоугольника, получим их равнодействующую R*, равную геометрической сумме заданных сил и приложенную в центре приведения О:
R* = F1''+F2''+F3'' = F1+F2+F3.
Геометрическая сумма всех сил системы называется главным вектором системы сил и в отличие от равнодействующей R обозначается R*.
Рис. 3.6
Складывая пары F1 F1 ', F2, F '2; F3, F '3, получим эквивалентную им пару сил. Момент каждой присоединенной пары сил равен моменту соответствующей силы относительно центра приведения:
M1 = M10 = r1×F1; M2 = M20 = r2×F2; M3 = M30 = r3×F3.
Момент пары сил, эквивалентной трем присоединенным парам сил, равен геометрической сумме моментов этих пар.
Строя многоугольник моментов присоединенных пар, находим
M = M1+M2+M3 = M10+M20+M30 = M0 ,
т. е. момент пары сил, эквивалентной трем присоединенным парам, равен главному моменту этих трех сил относительно центра приведения.
Распространяя полученные результаты на любое число сил, произвольно расположенных в пространстве, имеем
R*=
.
Этот результат можно сформулировать следующим образом: силы, произвольно расположенные в пространстве, можно привести к одной силе, равной их главному вектору и приложенной в центре приведения, и к паре сил с моментом, равным главному моменту всех сил относительно центра приведения.
Выбор центра приведения не отражается на модуле и направлении главного вектора R*, но влияет на модуль и направление главного момента Мо.
Пользуясь методом приведения произвольной системы сил к заданному центру, рассмотрим вопросы, связанные с системами сил, произвольно расположенных на плоскости.
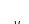
Рис. 3.7
Для вычисления главного вектора R* системы сил, произвольно расположенных на плоскости, воспользуемся методом проекций. На рис. 3.7 показано приведение к центру О трех сил F1 F2, F3. Известно, что
R*=F1+F2+…+Fn .
Обозначив Rx, Ry проекции главного вектора на оси координат, получим
Rx =F1x+F2x+…+Fnx
Ry =F1y+F2y+…+Fny
где F1x, F2x, ..., Fnx; F1y, F2y, Fny – проекции сил F1, F2, …, Fn соответственно на оси x и y.
Модуль и направление главного вектора R* определяются по формулам
.
Все присоединенные пары сил лежат в одной плоскости.
Момент эквивалентной им пары сил, равный главному моменту системы сил относительно центра приведения, определяется согласно как алгебраическая сумма моментов сил относительно этого центра.
М
= М0=
.