10. Теорема о среднем значении функции:
Если функция f(x) интегрируема на отрезке [a, b] и удовлетворяет на этом отрезке неравенствам m f(x) M , то существует число μ, m M, такое, что
.
Доказательство:
1) Пусть a < b , тогда по свойству 9
.
Разделим все части неравенств на
>0:
.
Обозначим число
за ,
то есть
=
.
Тогда m M и .
2) Пусть теперь b < a. Тогда по доказанному выше
или
или
.
Следствие: Если функция f(x) непрерывна на отрезке [a, b], то на этом отрезке найдется хотя бы одна точка с, такая что
.
Доказательство:
Так как функция f(x)
непрерывна на отрезке [a,
b], то по второй
теореме Вейерштрасса она достигает на
этом отрезке своего наибольшего М
и наименьшего m
значений. Это значит, что
,
m
f(x)
M
. В этом случае выполнены все условия
теоремы о среднем, и по этой теореме
найдется число
, m
M, такое что
.
Так как промежуточное значение между m и M , а f(x) непрерывна на отрезке [a, b], то по второй теореме Больцано-Коши найдется хотя бы одна точка с, такая что f(с)= . Подставив это в последнее равенство, получим:
.
Замечание: Теорема о среднем в исходной формулировке допускает следующее геометрическое истолкование.
Пусть f(x) 0 на [a, b].
численно равен площади криволинейной
трапеции.
Рассмотрим прямоугольник abBA
с тем же основанием, что и у криволинейной
трапеции, и высотой, равной значению
функции, определенному по теореме о
среднем. Произведение
численно равно площади прямоугольника
abBA. Следовательно,
криволинейная трапеция равновелика
прямоугольнику с тем же основанием, а
высотой, равной значению подынтегральной
функции в «средней» точке с.
§ 8. Интеграл как функция верхнего предела. Существование первообразной от непрерывной функции
Отметим, что значение определенного интеграла не зависит от обозначения переменной интегрирования, то есть
Это свойство становится особенно ясным, если трактовать определенный интеграл как площадь. Площадь криволинейной трапеции не зависит от наименования координат, к системе которых отнесен график подынтегральной функции.
Пусть функция f(x) интегрируема на [a, b] и х - произвольная точка, принадлежащая отрезку [a, b]. По свойству 3 определенного интеграла функция f(x) будет интегрируема и на отрезке [a, х].
Рассмотрим
.
Ясно, что при изменении верхнего предела
х будет меняться величина интеграла,
то есть интеграл является функцией
своего верхнего предела х. Обозначим
его через Φ (х), то есть
Φ (х)= .
Изучим свойства этого интеграла.
Теорема 1:
Если
функция f(x)
интегрируема на отрезке [a,
b], то функция
Φ (х)=
непрерывна
на этом отрезке.
Доказательство:
Возьмем любой
,
придадим х приращение х
такое, что х+х
.
Рассмотрим приращение DΦ:
.
Таким образом,
=
(1)
Функция f(t)
интегрируема на отрезке [x,
x+x],
следовательно, она будет и ограничена
на этом отрезке. Это значит, что для всех
t из
этого отрезка,
.
Тогда выполняются все условия теоремы
о среднем. Применив ее, получим
Если Dх→0, то с изменением отрезка [x, x+x] будут меняться числа m/ и M / , поэтому и будет меняться.
Пока трудно сказать, как будет вести себя правая часть равенства (1).
Заметим, что если
M
и m
– ТВГ и ТНГ
множества значений {f(x)}
функции y=f(x)
на отрезке [a,
b], то M
M
/
, m
m/.
Поэтому
,
то есть - величина
ограниченная. Если Dх→0,
то Dх→0,
тогда и
→0.
Значит
непрерывна
в точке х, а так как х произвольная
точка отрезка [a, b],
то это и доказывает теорему.
Теорема 2:
Если функция f(x) интегрируема на отрезке [a, b], то функция Φ(х) дифференцируема на этом отрезке и ее производная равна значению подынтегральной функции в точке, равной верхнему пределу, то есть
.
Доказательство:
Придадим х приращение Φ(х),
по определению производной
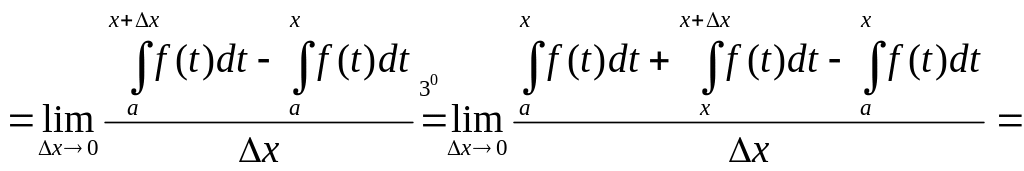
Например:
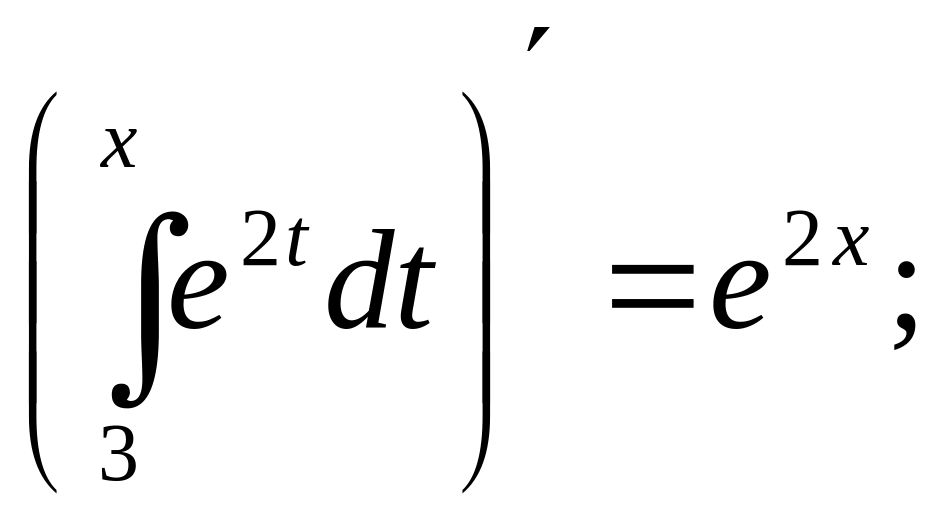
Таким образом интеграл с переменным верхним пределом является одной из первообразных подынтегральной функции.
Следствие: Если f(x)
непрерывна на [a, b],
то она имеет на этом отрезке первообразную.
Такой первообразной является, например,
.
Замечание: Аналогичными свойствами
обладает интеграл как функция нижнего
предела, то есть
.
В этом случае имеем
