67

Федеральное агентство по образованию Государственное образовательное учреждение

высшего профессионального образования

«Бийский педагогический государственный университет

имени В. М. Шукшина»

Кафедра математики и

методики обучения математике

В.Г. Заворуева, А.А. Сироткина, Р.А. Комаров

Определенный интеграл

Методические рекомендации

для студентов педвузов

Бийск

БПГУ им. В. М. Шукшина

2008

ББК 22.1

З 13

Печатается по решению редакционно-издательского совета

Бийского педагогического государственного университета

им. В.М. Шукшина

Рецензенты:

канд. физ.-мат. наук, доцент кафедры высшей математики

и математической физики БТИ Л.В. Китаева (г. Бийск);

канд. физ.-мат. наук, доцент кафедры

математики и методики обучения математике

БПГУ Т. Д. Васильева (г. Бийск).

З 13 Заворуева, В. Г.

Определенный интеграл [Текст]: методические рекомендации для студентов педвузов / В. Г. Заворуева, А. А. Сироткина, Р. А. Комаров; Бийский пед. гос. ун-т им. В. М. Шукшина. – Бийск: БПГУ им. В. М. Шукшина, 2008. – 65 с. - 100 экз.

Методические рекомендации содержат краткий теоретический материал и решение конкретных примеров по теме «Определенный интеграл». Во второй части рекомендаций предлагается 27 вариантов индивидуального задания.

Методические рекомендации предназначены для студентов физико-математического факультета специальностей 050201.65, 050203.65.

© БПГУ им. В. М. Шукшина, 2008.

§ 1. Задачи, приводящие к понятию определенного интеграла

1). Площадь криволинейной трапеции.

Пусть требуется найти площадь фигуры, ограниченной сверху непрерывной кривой у=f(х), снизу – осью ОХ, слева и справа – прямыми х=а, x=b (такая фигура называется криволинейной трапецией).

Разобьем отрезок [a, b] произвольным образом на n частей точками деления x₁ , x₂ ,…, x_n-1, причем

a=x₀<x₁ <…<x_n=b.

Проведем через точки деления прямые, параллельные оси ОУ. Таким образом мы разбили криволинейную трапецию на n элементарных криволинейных трапеций. Площадь данной криволинейной трапеции равна сумме площадей всех n элементарных криволинейных трапеций. Поэтому, если обозначить через S площадь данной криволинейной трапеции, а через S_i – площадь i-ой элементарной криволинейной трапеции с основанием на отрезке [x_i-1, x_i], где i=1, 2,…n, то S=S₁+S₂+…+S_n .

Но вычислить площадь элементарных трапеций так же трудно, как и данной. Поэтому поступим следующим образом: на каждом отрезке [x_i-1, x_i] (i=1, 2,…,n) выберем произвольную точку ξ_i ( ) и найдем в этой точке значение функции f(ξ_i). Заменим теперь каждую элементарную криволинейную трапецию с основанием

[x_i-1, x_i] (i=1,…,n) прямоугольником с тем же основанием, а высотой равной f(ξ_i). Площадь i-го прямоугольника будет равна:

f(ξ_i)(x_i – x_i-1 ).

Причем площадь этого прямоугольника заменяет приближенно значение площади элементарной криволинейной трапеции, то есть

S_i  f(ξ_i)(x_i – x_i-1 ).

Заменив площадь каждой элементарной криволинейной трапеции площадью прямоугольника с тем же основанием и высотой, равной ординате кривой в некоторой произвольной точке основания, получим ступенчатую фигуру. Площадь этой ступенчатой фигуры дает нам приближенное значение площади S криволинейной трапеции:

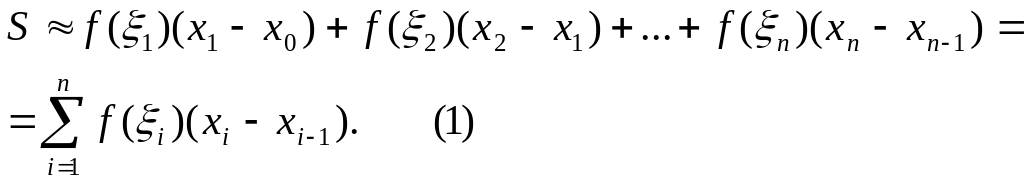
Обозначим за λ наибольшую из длин элементарных отрезков разбиения, то есть

.

С уменьшением λ точность приближенной формулы (1) увеличивается. Поэтому вполне естественно за точное значение площади S криволинейной трапеции принять предел последовательности площадей ступенчатых фигур при условии, что наибольшее из длин λ элементарных отрезков стремится к нулю, таким образом

.

Если обозначить x_i – x_i-1 =∆x_i , то последняя формула примет вид:

.