8. Дать оценку влияния факторов на результат с помощью коэффициентов эластичности, бета– и дельта– коэффициентов.

Средние коэффициенты эластичности в случае линейной модели определяются формулами

, j = 1, 2, … ,

где - выборочные средние признаков X_j и Y; - коэффициенты регрессии.

Подготовим (функция СРЗНАЧ)

и найдем , .

Следовательно, при увеличении цены нового автомобиля Х₁ на 1% и неизменном уровне срока эксплуатации цена реализации Y увеличивается в среднем на 1,18%.

Увеличение срока эксплуатации Х₂ на 1% приводит к снижению цены реализации Y в среднем на 0,25% (при неизменной цене нового автомобиля).

Бета-коэффициенты определяются формулами

,

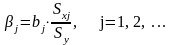где - выборочные средние квадратичные (стандартные) отклонения признаков X_j и Y; - коэффициенты регрессии.

Подготовим

(функция СТАНДОТКЛОН) и рассчитаем ,

Таким образом, при увеличении только фактора Х₁ на одно свое стандартное отклонение результат Y увеличивается в среднем на 0,86 своего стандартного отклонения S_y, а при увеличении только фактора Х₂ на одно его стандартное отклонение – уменьшается на 0,19 S_y.

Дельта-коэффициенты определяются формулами

,

где - соответствующие выборочные коэффициенты парной корреляции.

Коэффициенты парной корреляции и найдены с помощью программы КОРРЕЛЯЦИЯ (п.1 данной задачи), коэффициент детерминации определен для рассматриваемой двухфакторной модели программой РЕГРЕССИЯ.

Вычислим дельта-коэффициенты

.

Значит, по уравнению полученной линейной двухфакторной модели (2) изменение результирующего фактора Y (цены реализации) на 91% объясняется воздействием фактора Х₁ (цена нового автомобиля) и на 9% влиянием фактора Х₂ (срок эксплуатации).

Задача 2

В таблице приведены данные по мировым ценам на нефть марки UK Brent ( в долл. за баррель) за 11 лет

t	1	2	3	4	5	6	7	8	9	10	11
Y	10,00	13,60	17,20	18,20	15,50	17,50	18,50	24,00	21,10	27,20	33,30

Требуется:

1. Построить линейную модель временного ряда , параметры которой оценить мнк. Пояснить смысл коэффициента регрессии.

С помощью программы «РЕГРЕССИЯ» найдем

	Коэффициенты
Y-пересечение	8,889091
t	1,792727

Таким образом, ; .

Модель построена, ее уравнение имеет вид .

Коэффициент регрессии показывает, что с каждым годом цена на нефть увеличивается в среднем на 1,79 долл. за баррель.

2. Оценить адекватность построенной модели, используя свойства случайности, независимости и соответствия остаточной компоненты нормальному закону распределения.

Проверка перечисленных свойств состоит в исследовании Ряда остатков , который содержится в таблице «Вывод остатка» итогов РЕГРЕССИИ.

Наблюдение	Предсказанное Y	Остатки
1	10,68182	-0,68182
2	12,47455	1,125455
…	…	…
10	26,81636	0,383636
11	28,60909	4,690909

Для проверки свойства случайности остаточной компоненты используем критерий поворотных точек (пиков), основой которого является определение количества поворотных точек для ряда остатков.

С помощью Мастера диаграмм построим график остатков .

Поворотными считаются точки максимумов и минимумов на этом графике (в данном случае – третья, пятая, шестая, седьмая, восьмая и девятая). Их количество .

По формуле при вычислим критическое значение .

Сравним значения p и p_кр и сделаем вывод согласно схеме:

> , следовательно, свойство случайности для ряда остатков выполняется.

Для проверки свойства независимости остаточной компоненты используем критерий Дарбина-Уотсона.

Согласно этому критерию вычислим по формуле статистику

.

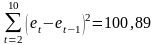Подготовим для вычислений: (функция СУММКВ), (функция СУММКВРАЗН).

Таким образом, .

По таблице d – статистик Дарбина – Уотсона (Приложение 4) определим критические уровни: нижний d₁ = 0,93 и верхний d₂ = 1,32.

Сравним полученную фактическую величину d с критическими уровнями d₁ и d₂ и сделаем вывод согласно схеме:

, следовательно, свойство независимости остатков для построенной модели выполняется.

Для проверки соответствия ряда остатков нормальному закону распределения используется R/S критерий.

В соответствии с этим критерием вычислим по формуле статистику

.

Подготовим для вычислений:

- максимальный уровень ряда остатков (функция МАКС);

- минимальный уровень ряда остатков (функция МИН);

- стандартная ошибка модели (таблица «Регрессионная статистика» вывода итогов РЕГРЕССИИ).

Получим .

По таблице критических границ отношения R/S (Приложение 5) определим критический интервал. При можно использовать .

Сопоставим фактическую величину R/S с критическим интервалом и сделаем вывод согласно схеме:

, значит, для построенной модели свойство нормального распределения остаточной компоненты выполняется.

Проведенная проверка показывает, что для построенной модели выполняются все свойства. Таким образом, данная трендовая модель является адекватной реальному ряду наблюдений, её можно использовать для построения прогнозных оценок.