2. Построить модель парной регрессии с наиболее информативным фактором; дать экономическую интерпретацию коэффициента регрессии.

Для построения парной линейной модели используем программу РЕГРЕССИЯ (Данные / Анализ данных). В качестве «входного интервала Х» покажем значения фактора Х₁.

Результаты вычислений представлены в таблицах:

ВЫВОД ИТОГОВ
Регрессионная статистика
Множественный R			0,910987272
R-квадрат			0,82989781
Нормированный R-квадрат			0,815722627
Стандартная ошибка			2,221570556
Наблюдения			14
Дисперсионный анализ
	df	SS		MS		F	Значимость F
Регрессия	1	288,9456626		288,9456626		58,54583	5,91E-06
Остаток	12	59,22450883		4,935375735
Итого	13	348,1701714

	Коэффициенты	Стандартная ошибка	t - статистика	P-зна-чение	Нижние 95%	Верхние 95%
Y-пересечение	-3,709033	2,513834	-1,47544	0,16584	-9,1862	1,76814
X	0,840183	0,109806	7,65152	5,91E-06	0,60093	1,07942

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y		Остатки
1	8,045121		0,284879
2	12,296445		-1,896445
3	10,876537		-0,276537
4	17,295531		-0,715531
5	17,673614		3,266386
6	23,017175		-3,887175
7	15,220280		-1,340280
8	9,935532		-1,135532
9	10,187587		3,702413
10	12,288043		-1,258043
11	15,287495		-0,407495
12	19,446399		0,983601
13	15,203477		-0,403477
14	22,966764		3,083236

Коэффициенты модели содержатся в третьей таблице итогов РЕГРЕССИИ (столбец Коэффициенты).

Таким образом, модель парной регрессии (модель 1) построена, ее уравнение имеет вид

.

Коэффициент регрессии , следовательно, при увеличении цены нового автомобиля (Х₁) на 1 тыс.у.е. цена реализации (Y) увеличивается в среднем на 0,84 тыс.у.е.

Свободный член в данном уравнении не имеет реального смысла.

3. Оценить качество модели с помощью средней относительной ошибки аппроксимации, коэффициента детерминации и F – критерия Фишера (принять уровень значимости α=0,05).

Для вычисления средней относительной ошибки аппроксимации рассмотрим остатки модели , содержащиеся в столбце Остатки итогов программы РЕГРЕССИЯ (таблица «Вывод остатка»). Дополним таблицу столбцом относительных погрешностей, которые вычислим по формуле 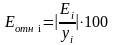с помощью функции ABS.

ВЫВОД ОСТАТКА
Наблюдение	Предсказанное Y	Остатки	Отн. погр-ти
1	8,045121	0,284879	3,419912
2	12,296445	-1,896445	18,235049
…	…	…	…
13	15,203477	-0,403477	2,726195
14	22,966764	3,083236	11,835840

По столбцу относительных погрешностей найдем среднее значение 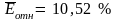(функция СРЗНАЧ).

Оценим точность построенной модели в соответствии со схемой:

– модель (1) имеет удовлетворительную точность.

Коэффициент детерминации R-квадрат определен программой РЕГРЕССИЯ (таблица «Регрессионная статистика») и составляет

Таким образом, вариация (изменение) цены реализации Y на 82,99% объясняется по уравнению модели вариацией цены нового автомобиля Х₁.

Проверим значимость полученного уравнения с помощью F – критерия Фишера.

F – статистика определена программой РЕГРЕССИЯ (таблица «Дисперсионный анализ») и составляет F = 58,55.

Критическое значение F_кр= 4,75 найдено для уровня значимости =5% и чисел степеней свободы k₁=1, k₂=12 (Приложение 2 или функция FРАСПОБР).

Схема проверки:

Сравнение показывает: F = 58,55 > F_кр = 4,75; следовательно, уравнение модели является значимым, его использование целесообразно, зависимая переменная Y достаточно хорошо описывается включенной в модель факторной переменной Х₁.

4. С доверительной вероятностью γ=90% осуществить прогнозирование среднего значения показателя Y в предположении, что прогнозное значение фактора Х увеличится на 20% от его среднего значения. Представить графически фактические и модельные значения Y, результаты прогнозирования.

Согласно условию задачи прогнозное значение факторной переменной Х₁ составляет . Рассчитаем по уравнению модели прогнозное значение показателя Y:

.

Таким образом, если цена нового автомобиля увеличится на 20% от среднего значения и составит 26,69 тыс.у.е., то ожидаемая цена реализации будет около 18,72 тыс.у.е.

Зададим доверительную вероятность и построим доверительный прогнозный интервал для среднего значения Y.

Для этого нужно рассчитать стандартную ошибку прогнозирования для среднего значения результирующего признака

.

Предварительно подготовим:

- стандартную ошибку модели (таблица «Регрессионная статистика» итогов РЕГРЕССИИ);

- по столбцу исходных данных Х₁ найдем среднее значение (функция СРЗНАЧ) и определим (функция КВАДРОТКЛ);

- (Приложение 1 или функция СТЬЮДРАСПОБР).

Следовательно, стандартная ошибка прогнозирования для среднего значения составляет

.

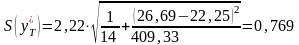Размах доверительного интервала для среднего значения

.

Границами прогнозного интервала будут

;

.

Таким образом, с надежностью 90% можно утверждать, что если цена нового автомобиля увеличится на 20% от среднего значения и составит 26,69 тыс.у.е., то ожидаемая средняя цена реализации будет от 17,35 тыс.у.е. до 20,09 тыс.у.е.

Для построения чертежа используем Мастер диаграмм (точечная) – покажем исходные данные (поле корреляции).

Затем с помощью опции Добавить линию тренда… построим линию модели:

тип → линейная; параметры → показывать уравнение на диаграмме.

Покажем на графике результаты прогнозирования. Для этого в опции Исходные данные добавим ряды:

Имя → прогноз; значения Х → х^*; значения Y → у^*;

Имя → нижняя граница; значения Х → х^*; значения Y → U_нижн;

Имя → верхняя граница; значения Х → х^*; значения Y → U_верх.