2.4. Формула Эйлера. Показательная форма комплексного числа.

Введём следующее обозначение:

e^i=cos+isin. (2.4.1).

Формула (2.4.1) называется формулой Эйлера. Тогда комплексное число =||(cos+isin) запишется в виде

=||e^i. (2.4.2)

Формула (2.4.2) называется показательной формой комплексного числа .

2.4.1. Упражнение. Представить в показательной форме комплексные числа из упражнения 2.3.1.

Решение. б) Мы видели, что 4=4(cos+isin.). Поэтому 4=4e^i.

з) Так как 1+ i=2(cos +isin ), то 1+ i=2 .

Ответ: б) 4=4e^i; з) 1+ i=2 .

2.5. Корни из комплексного числа и их вычисление.

2.5.1. Определение. Пусть n  натуральное число. Корнем n-й степени из комплексного числа  называется такое комплексное число , что =.

Корень n-й степени из комплексного числа  обозначается через .

2.5.2. Теорема. Существует в точности n различных значений корня n-й степени из комплексного числа . Они вычисляются по формуле

= (cos +isin ), (2.5.1)

где r  модуль числа ,   его аргумент, l  произвольное целое число, k пробегает все значения от 0 до n1.

Таким образом, множество значений корня n-й степени  следующее

= (cos +isin . (2.5.2)

2.5.3. Упражнение. Вычислить:

а) ; б) ; в) ; г) ; д) ; е) ;

ж) ; з) .

Решение. б) Найдём тригонометрическую форму числа 1: 1= =cos+isin. Тогда по (2.5.2) имеем

={_k=cos +i sin | k=0, 1, 2, 3}.

Найдём каждое значение _k в отдельности:

₀=cos +i sin = + i;

₁=cos +i sin =cos +i sin =  + i;

₂=cos +i sin =cos +i sin =   i;

₃=cos +i sin =cos +i sin =  i;

Ответ: б) ={ + i,  + i,   i,  i}.

2.5.4. Вычисление квадратного корня из комплексного числа в большинстве случаев удобно производить по следующей схеме. Пусть требуется найти . Будем искать в виде x+yi:

=x+yi. (2.5.3).

Возведём обе части (2.5.3) в квадрат: a+bi=(x²y²)+2xyi. Теперь, приравняв в обеих частях действительные и мнимые части, приходим к системе

решая которую, находим x и y.

Например, пусть требуется найти . Положим = =x+yi, откуда получаем 28+8i=(x²y²)+2xyi и приходим к системе

Выражая из второго уравнения y через x (y= ) и подставляя его в первое, приходим к уравнению x² =28, которое приводится к виду x⁴+28x²16=0. Оно  биквадратное. Положим t=x² и решим полученное квадратное уравнение t²+28t16=0. Получаем решения: t₁=14+2 и t₁=142 . Второе отбрасываем из рассмотрения, так как x= должен быть действительным. Поэтому x_1,2= . Отсюда y_1,2= , то есть

={ + i,   i}.

2.5.5. Упражнение. Вычислить , , , .

2.5.6. Можно показать, что квадратное уравнение ax²+bx+c=0, где a, b, cC, имеет корни .

2.5.7. Упражнение. Решить уравнения:

а) x²1=0; б) x²+2=0; в) x²2i=0; г) x²+2x+2=0;

д) x²+(2+i)x+(32i)=0; е) 4x²(2i)x+(62i)=0.

Решение. д) Корнями являются числа

x_1,2= .

Найдём отдельно выражение под корнем:

(2+i)²4(32i)=4+4i112+8i=8+12i.

Поэтому = . Этот корень будем искать по правилу, изложенному в 2.5.4:

8+12i=(x²y²)+2xyi, откуда Далее, опуская комментарии, имеем y= , x² =8, x⁴+8x²36=0, t=x², t²+8t36=0, D=8²4(36)=208=1613, t=2 4, t_{1, 2}= =42 , x= , y= , =( + i). Теперь

x_1,2= = =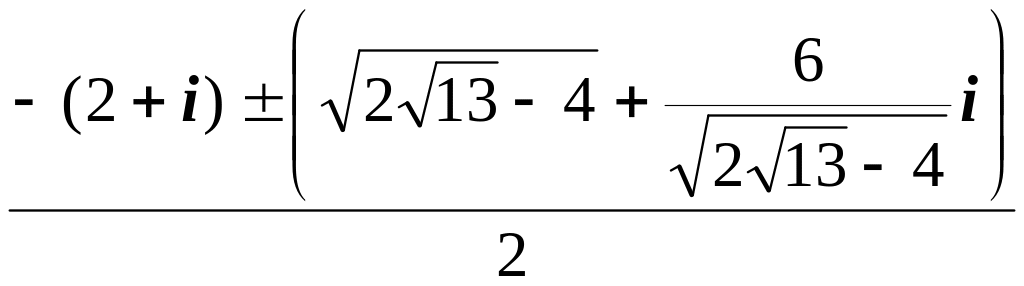

= =

= .

Ответ. x₁= ,

x₂= .

1 Понятие «множество», другие понятия и обозначения,связанные с ним, см. Приложение 3.

2 Ниже в угловых скобках мелким шрифтом приводятся комментарии к преобразованиям