Практическая работа №2 по теме 1.2 Системы линейных уравнений

Содержание учебного материала. Решение системы линейных уравнений методом определителей (по правилу Крамера), методом обратной матрицы и методом Гаусса.

Цель работы: закрепить знания, умения и навыки по решению систем линейных уравнений методом (СЛУ и СЛОУ) определителей (по правилу Крамера), методом обратной матрицы и методом Гаусса.

Литература:

[ ОЛ-1 ] Глава 2, § 2.4, стр. 37 - 52,

[ ОЛ-2 ] Глава 2, § 2.3, стр. 13 - 19

Вопросы для повторения:

1. Определение СЛУ и СЛОУ.

2. Матрица, ступенчатая матрица.

3. Определитель.

4. Ранг матрицы.

5. Сущность метода определителей (правила Крамера) в решении СЛУ.

6. Сущность метода обратной матрицы в решении СЛУ.

7. Сущность метода Гаусса в решении СЛУ.

Указания к выполнению работы: используя матрицы, предложенные в варианте, запишите предварительно систему в виде где матрицы A, B и X имеют вид: , , .

Задания:

1. Решить СЛУ методом определителей (по правилу Крамера).

2. Решить СЛУ методом обратной матрицы.

3. Решить СЛУ методом Гаусса.

Вариант	Матрица А	Матрица В	Вариант	Матрица А	Матрица В
1			6
2			7
3			8
4			9
5			10

Практическая работа №3 по теме 2.1 Теория пределов. Непрерывность функции

Содержание учебного материала. Вычисление пределов с помощью замечательных пределов, раскрытие неопределенностей. Вычисление односторонних пределов, классификация точек разрыва.

Цель работы: закрепить знания, умения и навыки по применению замечательных пределов к решению пределов другого вида, по раскрытию неопределенностей вида 0/0 и ∞/∞, по решению односторонних пределов; закрепить умение определять вид точек разрыва.

Литература:

[ ОЛ-1 ] Глава 2, § 5.1 – 5.5, стр. 97 - 115,

[ ОЛ-2 ] Глава 5, § 5.1 – 5.2, стр. 53 - 58

[ ОЛ-3 ] Глава 6, § 1 - 6, стр. 76 – 86

Вопросы для повторения:

1. Определение предела.

2. Свойства предела.

3. Определение бесконечно малой и бесконечно большой величины.

4. Замечательные пределы.

5. Односторонние пределы.

6. Определение функции, непрерывной в точке и на промежутке.

7. Определение точки разрыва функции.

8. Классификация точек разрыва функции.

Указания к выполнению работы: составьте предел или функцию, используя предложенные в варианте параметры.

Вариант	Параметры			Вариант		Параметры
	a	b	c			a	b	c
1	1	-15	1		6		4	-12	7
2	-1	15	2		7		-4	12	8
3	2	-14	3		8		5	-11	9
4	-2	14	4		9		-5	11	10
5	3	-13	5		10		6	-10	11

Задания:

1. Вычислить предел.

а)		з)
б)		и)
в)		к)
г)		л)
д)		м)
е)		н)	.
ж)		о)

2. Исследовать функцию на непрерывность в точке или на промежутке, определить вид точек разрыва функции при их наличии. В задании г) постройте график функции

а) , ; б) ;

в) ; г)
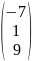