5 Приложения методов финансовой математики в финансово-кредитных операциях

5.1 Методы расчета лизинговых платежей.

Под лизингом (leasing) понимают вид предпринимательской деятельности, который заключается в инвестировании финансовых средств путем приобретения производственного имущества для последующей сдачи в аренду. Лизинг - это специального вида аренда имущества производственного назначения.

В любом лизинговом контракте участвуют, как минимум, две стороны – лизингодатель и лизингополучатель.

Лизингодатель (арендодатель , less or) передает право пользования имуществом на фиксированный в контракте срок. Лизингополучатель (арендатор, lessee) платит оговоренные арендные или лизинговые платежи.

По способу приобретения объекта лизинга различают:

• прямой лизинг (direct lease) – оборудование приобретается за собственные средства, по согласованной цене.

• leveraged lease – приобретается оборудование за счет привлеченных средств.

Лизинг также бывает финансовый или оперативный.

Финансовый или капитальный лизинг (finance, capital lease). Данный вид аренды предусматривает полное возмещение всех расходов лизингодателя на приобретение имущества и его передачу для производственного использования лизингополучателю.

Частным случаем финансового лизинга является возвратный лизинг (sale and leaseback). Он предполагает продажу объекта лизинга и получение его обратно у нового владельца в порядке финансового лизинга. Вместе с отказом от права собственности бывший владелец получает средства для финансирования других своих нужд. Кроме того, арендатор имеет возможность сократить налоговые выплаты, связанные со стоимостью арендованного имущества.

Оперативный лизинг (operating lease). Оперативный лизинг характеризуется короткими сроками, что предполагает возможность неоднократной сдачи объекта лизинга в аренду.

При математическом анализе лизинговой операции необходимо определить размер лизинговых платежей, а следовательно, финансовую эффективность операции.

Лизингодатель заинтересован в том, чтобы лизинговые платежи полностью покрыли его издержки: расходы по закупке оборудования, кредитованию, страхованию, по подготовке контракта, а также и прибыль.

Способы оплаты по лизинговым контрактам могут быть различны, так например, авансовые платежи, периодические выплаты, выкупная сумма.

Потоки лизинговых платежей есть не что иное, как финансовая рента; поэтому основой методов расчетов является теория финансовых рент (Раздел 4).

Лизинговые платежи различаются

по применяемой процентной ставке – сложная, простая, постоянная, переменная;

по сумме платежа – постоянная, переменная;

по сроку платежа – пренумерандо, постнумерандо;

по принадлежности – ежемесячно, ежеквартально и др.

Общее для всех схем является равенство настоящей стоимости лизингового потока затратам на приобретение объекта лизинга. Эта финансовая эквивалентность обязательств записывается уравнением

,

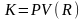где 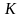– стоимость имущества для лизингодателя (с учетом таможенных сборов, страховых расходов и т.д.),

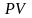- оператор определения современной стоимости,

- платежи по лизингу.

Рассмотрим методику расчета при различных видах лизинговых платежей.

• Платежи постоянны по времени и погашают всю стоимость имущества, причем выплаты постнумерандо.

В этом случае стоимость имущества для лизингодателя равна

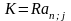
или 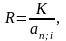где

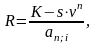
R – размер постоянного платежа по лизингу;

n –общее число платежей, (срок лизинга в месяцах, кварталах, годах);

i – процентная ставка ;

s – доля остаточной стоимости в первоначальной стоимости объекта лизинга;

a_n;I – коэффициент приведения постоянной ренты постнумерандо.

В практических расчетах часто применяют коэффициенты рассрочки платежей, показывающие долю стоимости оборудования, погашаемую при каждой выплате.

Коэффициент рассрочки в случае сложных процентов для постоянных рент постнумерандо обозначают

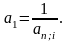или

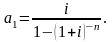
Коэффициент рассрочки в случае сложных процентов для постоянных рент пренумерандо обозначают

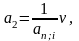где 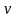-дисконтный множитель по ставке i

Размер лизингового платежа по лизингу равен

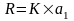(постнумерандо) или

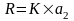(пренумерандо)

Замечание. Значения коэффициентов рассрочки при равных платежах при определенных сроках лизинга приведены в Приложении D.

• Пусть теперь первый платеж будет в k раз больше остальных (удвоен или утроен), причем соответственно сокращается число остальных платежей.

Тогда условие финансовой эквивалентности обязательств удовлетворяется следующими равенствами:

д ля выплат постнумерандо

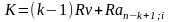
и для платежей пренумерандо

.

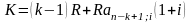Тогда лизинговые платежи

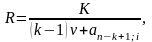
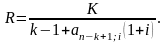
• Пусть предусмотрен авансовый платеж а.

Для лизинговых платежей постнумерандо и пренумерандо соответственно получим следующие уравнения эквивалентности:

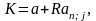(постнумерандо)

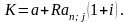(пренумерандо)

Для расчета лизинговые платежи R применим коэффициенты рассрочки.

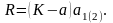
• Пусть предусмотрен

выкуп имущества по остаточной стоимости s , то уравнение эквивалентности при платежах постнумерандо имеет вид

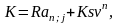
откуда

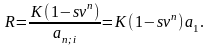
Аналогично для платежей пренумерандо получим

,

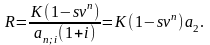где s – доля остаточной стоимости в первоначальной стоимости оборудования;

• Пусть имеет место авансовый платеж и выкуп имущества.

В этом случае для последовательностей платежей постнумерандо и пренумерандо имеем

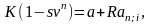
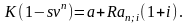
Соответственно, получим

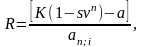или

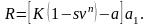
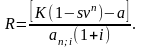
ПРИМЕР 35. Составить лизинговые контракты на три года, если стоимость оборудования равна 2000 у.е. под 2% в месяц; платежи постнумерандо, причем контракт предусматривает

а) полное погашение стоимости оборудования,

б) удвоенный взнос в первом месяце, освобождение от взноса в последнем

в) авансовый платеж 200 у.е.,

г) право выкупа в конце срока по цене 400 у.е.,

д) аванс и право выкупа.

Решение:

По условию задачи k = 2000,

n = 36 месяцев (3 года),

j = 2% в месяц,

тогда

а) по формуле 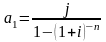найдем коэффициент рассрочки .

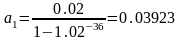Тогда размер ежемесячного платежа ,

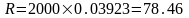В этом случае, сумма платежа за весь срок аренды составит

2824,56 у.е.

Прибыль лизингодателя составит 824,56 у.е.

Если платежи вносятся в начале месяца, то

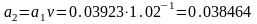
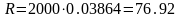, в этом случае прибыль в месяц

составит 2,13%.

б) удвоенный взнос в первом месяце (к=2).

Для взносов в конце периодов получим по формуле

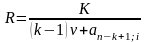
получим

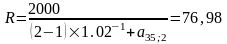
и первый взнос равен 2R=153,96 , остальные платежи вносятся ежемесячно по 76,98

в) Согласно условию в начале срока лизинга производится авансовый платеж в сумме 200 у.е.

Для расчета лизинговых платежей используем формулу

,

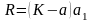Получим

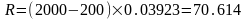
Таким образом, аванс – 200, остальные платежи по 70,614

г) Арендатор имеет право выкупить имущество к конце срока по цене 400 у.е.

Используем формулу

По условию нашей задачи сумма выкупа 400,

тогда 400/2000= 0.2, итак s=0,2 , ( )

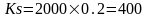и ежемесячные платежи составят

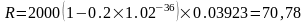
д) Если платежи арендатора следующие: аванс а=200 и выкупная цена 400, тогда по формуле

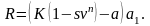
где s =0,2

находим