Практическая работа №10 по теме 3.3 Интегральное исчисление функции

Содержание учебного материала. Вычисление с помощью определенных интегралов площадей плоских фигур, объёмов тел вращения, длины дуги, площади поверхности тела вращения.

Цель работы: закрепить знания, умения и навыки по практическому применению интегралов.

Литература:

[ ОЛ-1 ] Глава 7, § 7.7, стр. 169 - 173,

[ ОЛ-2 ] Глава 7, § 7.3, стр. 84 - 88

[ ОЛ-3 ] Глава 13, § 1 - 6, стр. 212 – 227

Вопросы для повторения:

1. Определенный интеграл. Формула Ньютона-Лейбница

2. Криволинейная трапеция

3. Геометрический смысл определенного интеграла

4. Свойства определенного интеграла

Указания к выполнению работы: составьте интеграл, используя параметры своего варианта.

Вариант	Параметры			Вариант		Параметры
	a	b	с			a	b	с
1	2	3	1		6		2	3	-1
2	1	3	2		7		1	3	-2
3	1	2	1		8		3	4	-1
4	2	3	2		9		1	4	-2
5	2	4	2		10		2	3	-2

Задания

1. Вычислить площадь фигуры, ограниченной линиями:

а) , , , .

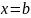б) , .

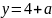2. Вычислить объем тела, полученного вращением вокруг оси Ох плоской фигуры, ограниченной линиями:

а) , , , .

б) ,

3. Вычислить длину дуги кривой от х = a до х = b .

Практическая работа №11 по теме 3.4 Дифференциальное исчисление функции нескольких действительных переменных

Содержание учебного материала. Нахождение области определения и вычисление пределов для функции нескольких переменных

Цель работы: закрепить знания, умения и навыки по нахождению области определения и вычислению пределов функции двух переменных.

Литература:

[ ОЛ-1 ] Глава 8, § 8.1 – 8.3, стр. 180 - 192,

[ ОЛ-2 ] Глава 8, § 8.1, стр. 92

[ ОЛ-3 ] Глава 29, § 2, стр. 438-439

Вопросы для повторения:

1. Функция нескольких переменных.

2. Частные производные функции нескольких переменных.

3. Частные дифференциалы функции нескольких переменных. Полный дифференциал.

Указания к выполнению работы: составьте функцию, используя параметры своего варианта.

Вариант	Параметры			Вариант		Параметры
	a	b	с			a	b	с
1	9	64	1		6		64	4	-1
2	25	16	2		7		16	16	-2
3	36	49	1		8		49	81	-1
4	49	9	2		9		9	25	-2
5	64	4	2		10		4	9	-2

Задания

1. Найти область определения функции:

а) 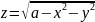; б)

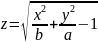
2. Найти частное значение функции:

а) в точке (4; с);

б) в точке (с; -3)

3. Вычислить предел функции: