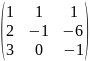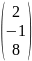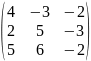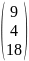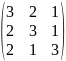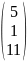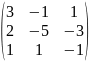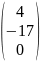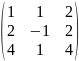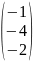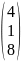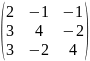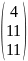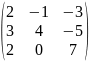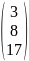Практическая работа №2 по теме 1.2 Системы линейных уравнений

Содержание учебного материала. Решение системы линейных уравнений методом определителей (по правилу Крамера), методом обратной матрицы и методом Гаусса.

Цель работы: закрепить знания, умения и навыки по решению систем линейных уравнений методом (СЛУ и СЛОУ) определителей (по правилу Крамера), методом обратной матрицы и методом Гаусса.

Литература:

[ ОЛ-1 ] Глава 2, § 2.4, стр. 37 - 52,

[ ОЛ-2 ] Глава 2, § 2.3, стр. 13 - 19

Вопросы для повторения:

1. Определение СЛУ и СЛОУ.

2. Матрица, ступенчатая матрица.

3. Определитель.

4. Ранг матрицы.

5. Сущность метода определителей (правила Крамера) в решении СЛУ.

6. Сущность метода обратной матрицы в решении СЛУ.

7. Сущность метода Гаусса в решении СЛУ.

Указания к выполнению работы: используя матрицы, предложенные в варианте, запишите предварительно систему в виде где матрицы A, B и X имеют вид: , , .

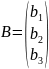Задания:

1. Решить СЛУ методом определителей (по правилу Крамера).

2. Решить СЛУ методом обратной матрицы.

3. Решить СЛУ методом Гаусса.

Вариант	Матрица А	Матрица В	Вариант	Матрица А	Матрица В
1			6
2			7
3			8
4			9
5			10

Практическая работа №3 по теме 2.1 Прямая на плоскости. Кривые второго порядка

Содержание учебного материала. Составление уравнений прямых и кривых 2-го порядка, их построение.

Цель работы: закрепить знания, умения и навыки по решению задач на составление уравнений прямых, по решению задач на взаимное расположение прямых в пространстве, по решению задач на составление уравнений кривых второго порядка, их построение.

Литература:

[ ОЛ-1 ] Глава 3, § 3.2 – 3.5, стр. 60 – 75

[ ОЛ-1 ] Глава 3, § 3.2 – 3.5, стр. 27 – 40

[ ОЛ-3 ] Глава 18, 19 § 1 - 10, стр. 286 – 326

Вопросы для повторения:

1. Общее уравнение прямой

2. Каноническое уравнение прямой

3. Уравнение прямой с нормальным вектором

4. Уравнение прямой, проходящей через две точки

5. Уравнение прямой в отрезках

6. Уравнение прямой с угловым коэффициентом

7. Взаимное расположение прямых на плоскости

8. Параллельность и перпендикулярность прямых на плоскости.

9. Окружность. Уравнение окружности с центром в начале координат и смещенным центром. Каноническое уравнение окружности.

10. Эллипс. Уравнение эллипса. Фокус. Эксцентриситет.

11. Гипербола. Уравнение гиперболы. Фокус. Эксцентриситет.

12. Парабола. Уравнение параболы с вершиной в начале координат и смещенной вершиной. Директриса параболы.

Указания к выполнению работы: составьте задачу, используя параметры своего варианта из таблицы 1, и решите её.

Таблица 1

Вариант	a	b	c	d	g	h
1	4	-2	8	-3	3	-6
2	5	-6	-4	-2	8	4
3	6	-7	7	-9	9	-8
4	7	-4	-3	-4	5	8
5	8	-5	5	-6	4	-1
6	3	-3	-6	4	-2	8
7	8	-2	4	5	-6	-4
8	9	-9	-8	6	-7	7
9	5	-4	8	7	-4	-3
10	4	-6	-1	8	-5	5

Задания:

1.Составить уравнение прямой, проходящей через точку А(a, b) параллельно вектору М₁М₂ = (g, h). Привести уравнение из канонического к общему виду.

2. Составить уравнение прямой, проходящей через точку В(c, d) перпендикулярно вектору М₁М₂. Привести уравнение к общему виду.

3. Определить взаимное расположение прямых АВ и М₁М₂.

4. Дан треугольник с вершинами А(a, b), В(c, d) и С(g, h). Составить уравнения медианы АD, высоты BK, прямой, параллельной стороне AB

Указания к выполнению работы: составьте задачу, используя параметры своего варианта из таблицы 2, и решите её.

Таблица 2

Вариант	a	b	f	R
1	2	-2	4	4
2	3	-4	5	6
3	4	-6	6	7
4	5	-8	7	3
5	6	-3	8	5
6	5	-2	7	6
7	3	-5	5	2
8	2	-4	4	1
9	4	-3	5	8
10	6	-5	8	4

Задания:

1.Составить каноническое уравнение окружности с центром в точке О(a, b) и радиусом R. Построить окружность

2. Составить уравнение эллипса, если его вершины находятся в точках А₁(a; 0) и А₂( a; 0), а фокусы – в точках F₁(f; 0) и F₂( f; 0). Построить эллипс

3. Составить уравнение гиперболы, если её вершины находятся в точках А₁(a; 0) и А₂( a; 0), а фокусы – в точках F₁(f; 0) и F₂( f; 0). Построить гиперболу.

4. Составить уравнение параболы с осью симметрии, параллельной оси Ох, если парабола проходит через точку М(a, b) и имеет вершину А(f; 0). Построить параболу.