ТАМБОВ
Автор: ТАРАСОВ В.Е., преподаватель спецдисциплин ТО ГАОУ СПО «Педагогический колледж г. Тамбова»
Рецензент: Лаппа Т.И.. заведующая отделением «Физическая культура» ТО ГАОУ СПО «Педагогический колледж г. Тамбова»
Техническая механика. Руководство по выполнению практических работ №1-№8.
Руководство по выполнению предназначено для студентов специальности 280707 «Защита в чрезвычайных ситуациях» при выполнении практических работ по учебной дисциплине «Техническая механика».
Пособие содержит необходимый теоретический и справочный материал для выполнения расчетных работ, приведены примеры решения типовых задач, варианты заданий.
Рекомендовано научно-методическим советом колледжа в качестве учебного пособия.
Практическая работа № 1 определение направления действия реакций связи
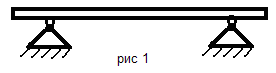
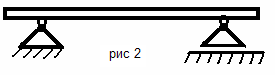
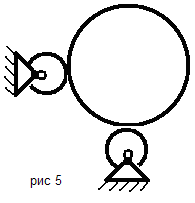
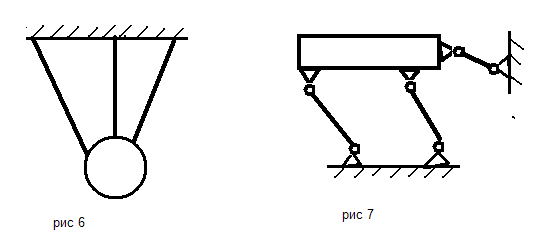
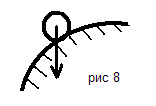
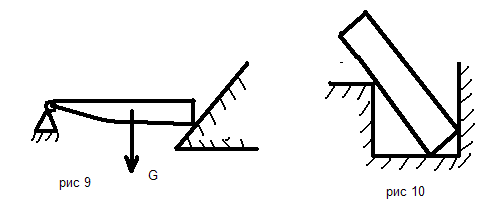
Определить направление действия реакций связи в механизмах и конструкциях на представленных рисунках № 1-10.
По результатам работы составить отчет, в котором на приведенных рисунках (рисунки выполнять карандашом, в соответствии с требованиями ЕСКД) в масштабе показать направления действия реакций связи в конструкциях. Работу выполнить на листе бумаги формата А4 с рамкой 20х5х5х5 мм и с основной надписью.
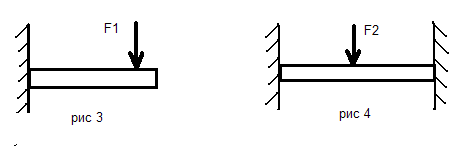
Практическая работа № 2 определение усилия в нитях и стержнях
Всякая система сходящихся сил может быть заменена равнодействующей. Всякая такая система сходящихся сил находится в равновесии, т.е. эквивалентна нулю, то равнодействующая должна равняться нулю.
Равенство нулю равнодействующей - необходимое и достаточное условие равновесие системы сходящихся сил. Соответственно двум способам определения равнодействующей (графическим и аналитическим) условие равновесия плоской системы сходящихся сил может быть выражено в двух формах:
УСЛОВИЕ РАВНОВЕСИЯ В ГЕОМЕТРИЧЕСКОЙ ФОРМЕ.
Геометрически
равнодействующая сходящих сил определяется
как замыкающая сторона силового
многоугольника.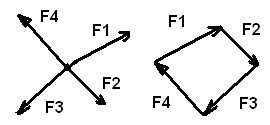 
Если
равнодействующая равна нулю, то нужно,
чтобы равнялась нулю и замыкающая
сторона и, следовательно, силовой
многоугольник замыкался сам на себя.
Отсюда получается следующее условие:
для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный для этой системы сил, был замкнутым.
Условие равновесия в аналитической форме.
Аналитический модуль равнодействующей силы определяется по формуле
F = √ (∑Xк)2 + (∑Yк)2
Где ∑Xк и ∑Yк – алгебраическая сумма проекций на оси векторов, составляющих сходящую систему сил.
Условие равновесия – модуль равнодействующей силы сходящейся системы сил равен нулю. F = 0
Но если F = 0, то равны нулю и подкоренные выражения:
∑ Xк = 0 и ∑Yк = 0
Эти уравнения называются уравнениями равновесия.
Для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы порознь равнялись нулю суммы проекций всех сил на каждую из двух любых взаимно перпендикулярных осей, лежащих в плоскости действия сил.
При решении задач о равновесии рекомендуется придерживаться следующего порядка:
Необходимо уяснить себе все условия задачи и что именно необходимо определить, чтобы все дальнейшие действия имели определенную целевую установку;
Тело, равновесие которого рассматривается, нужно освободить от связей, заменив последние соответствующими реакциями;
Придерживаясь некоторого масштаба, сделать схематичный чертеж, нанеся на него все активные силы и все реакции связей, приложенные к телу;
Используя условия равновесия этих сил (активные силы и силы реакций связей) в геометрической или аналитической форме записи определяем неизвестные реакции связей.
При решении задач аналитическим способом за начало координат удобно принимать ту точку, в которой сходятся силы, а координатные оси располагать так, чтобы проекции сил на эти оси находились наиболее просто.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ:
Между двумя стенами висит на тросах фонарь весом G = 20 Н. Левая нить троса образует со стеной угол ά = 450 , а правая – угол β= 30 0 Найти натяжение в нитях троса.
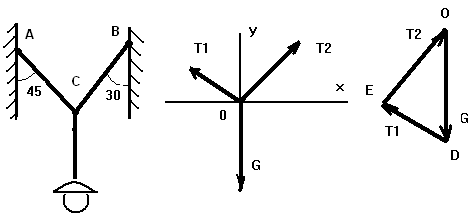
РЕШЕНИЕ: В задаче требуется определить натяжение нитей троса. Тросы натягиваются фонарем.
Активная сила – вес фонаря действует на точку С. Эта точка несвободна, связи осуществляются нитями тороса СА и СВ. Рассмотрим равновесие точки С. Освободив эту точку от связей и заменим и действие реакциями. Тогда точку С можно рассматривать как свободную и находящуюся в равновесии под действием трех сил: активной силы веса G и реакций нитей троса Т1 и Т2 , эти реакции численно равны искомым натяжениям троса.