Решение.

Обозначим угол наклона через , начальную скорость ядра – через , массу пушки – через .

Введем систему координат, связанную с наклонной плоскостью (см. рис.), а именно, начало координат совместим с первоначальным положением пушки, ось направим вдоль наклонной плоскости, а ось ‑ перпендикулярно ей.

Будем описывать движение ядра и пушки в этой системе координат.

Сперва рассмотрим движение пушки после выстрела. Силы, действующие на соскальзывающую пушку обозначены на рис. Напишем второй закон Ньютона для пушки в проекциях на оси:

,

,

откуда можно выразить ускорение пушки, исключив и . Так как , получаем, что ускорение пушки:

.

Рассмотрим теперь движение ядра. В используемой системе координат и по оси , и по оси ядро движется равноускоренно. Из рисунка видно, что проекции ускорения ядра на соответствующие оси , . Уравнения, описывающие движения ядра, следующие:

,

Из первого уравнения находим время полета ядра:

.

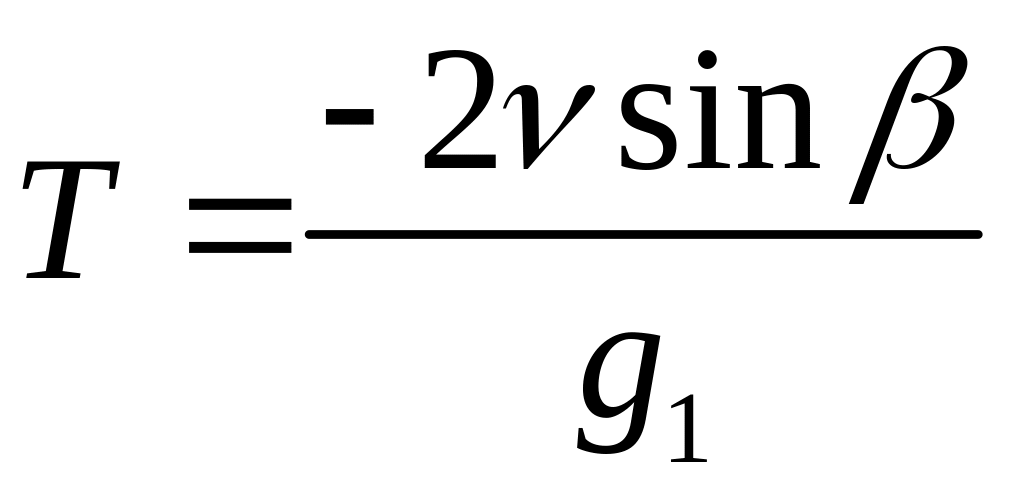В этот момент времени, ядро окажется в точке

,

а пушка съедет на расстояние

.

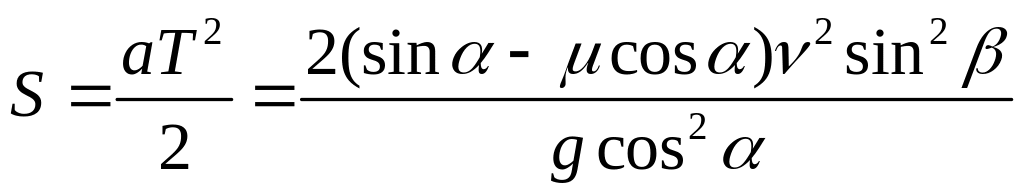Приравнивая и , после сокращения обоих множителей, получаем:

,

откуда

.

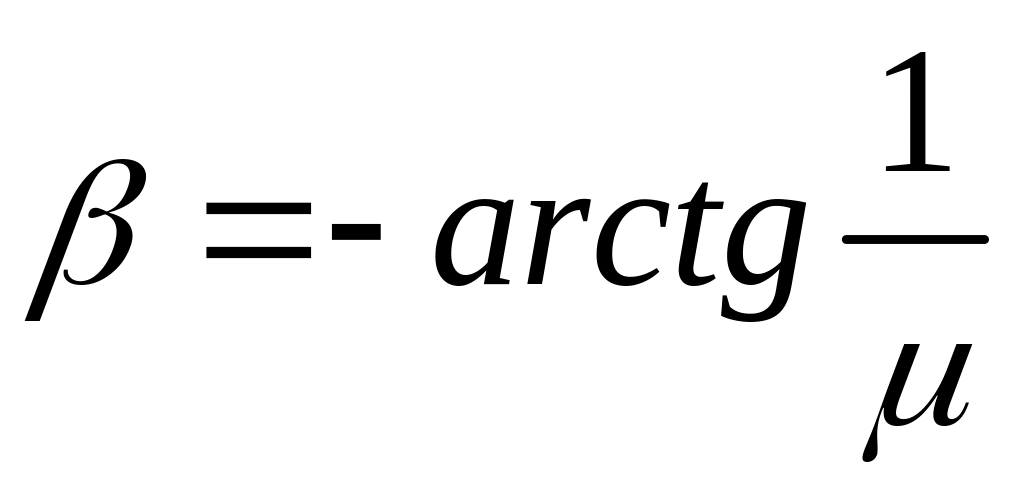Так как , угол всегда будет превосходить .

1. Записан второй закон Ньютона для пушки в проекциях на оси координат – 1 балл.

2. Найдено выражение для ускорения, с которым скатывается пушка – 1 балл.

3. Записаны зависимости координат ядра от времени – 1 балл.

4. Найдено время полета ядра – 1 балл.

5. Получено уравнение траектории ядра – 1 балл.

6. Сформулировано и записано условие попадания ядра в пушку – 2 балла.

7. Найден искомый угол – 2 балла.

8. Отмечено, что 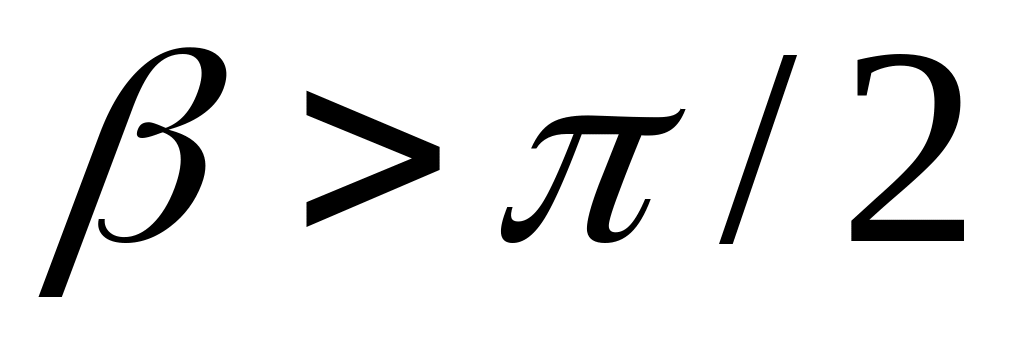– 1 балл.