9 класс

1. (10 баллов) Школьник прочитал в газете «Советы домохозяйке» следующую заметку. «Для того, чтобы рассортировать куриные яйца по степени свежести, возьмите четыре стеклянные банки, налейте в каждую пол-литра воды и растворите в первой банке 50 г соли, во второй – 45 г, в третьей – 30 г и в четвертой – 15 г. После этого поочередно опускайте яйца в каждую банку. В первой банке будут тонуть только что снесенные яйца, во второй – снесенные не более двух недель назад, в третьей – снесенные не более пяти недель назад, в четвертой – снесенные не более восьми недель назад.» Школьник сделал растворы, строго следуя рецепту, рассортировал имевшиеся в холодильнике яйца, а затем слил содержимое из всех четырех банок в одну большую емкость. Сколько недель назад снесены яйца, которые тонут в получившемся растворе?

Решение

Нарисуем график, вдоль горизонтальной оси которого отложим степень свежести яиц (в неделях), а вдоль вертикальной – концентрацию соли в растворе (в граммах на 0,5 литра воды). Видно, что на графике есть линейный участок, который свидетельствует о том, что в период с двух до восьми недель плотность яиц равномерно уменьшается со временем.

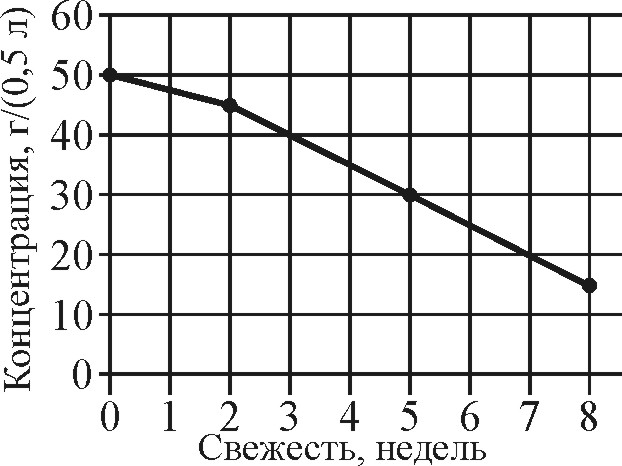
Далее найдем концентрацию соли в растворе, получившемся после сливания содержимого всех четырех банок в одну большую емкость. Эта емкость содержит 4 0,5л=2 литра воды и 50 г + 45 г +30 г + 15 г =140 г соли. Следовательно, концентрация соли в получившемся растворе равна 140 г/4=35 грамм на 0,5 литра. Из чертежа видно, что точка графика, соответствующая этой концентрации. Лежит на линейном участке графика. Это дает возможность, использовать график, определить свежесть яиц. Которые тонут в получившемся растворе – они снесены не более 4 недель назад.

1. Построен график зависимости – 6 баллов.

2. Указано наличие линейного участка – 1 балл.

3. Получен правильный ответ – 3 балла.

4. Если задача решена без графика – 3 балла.

2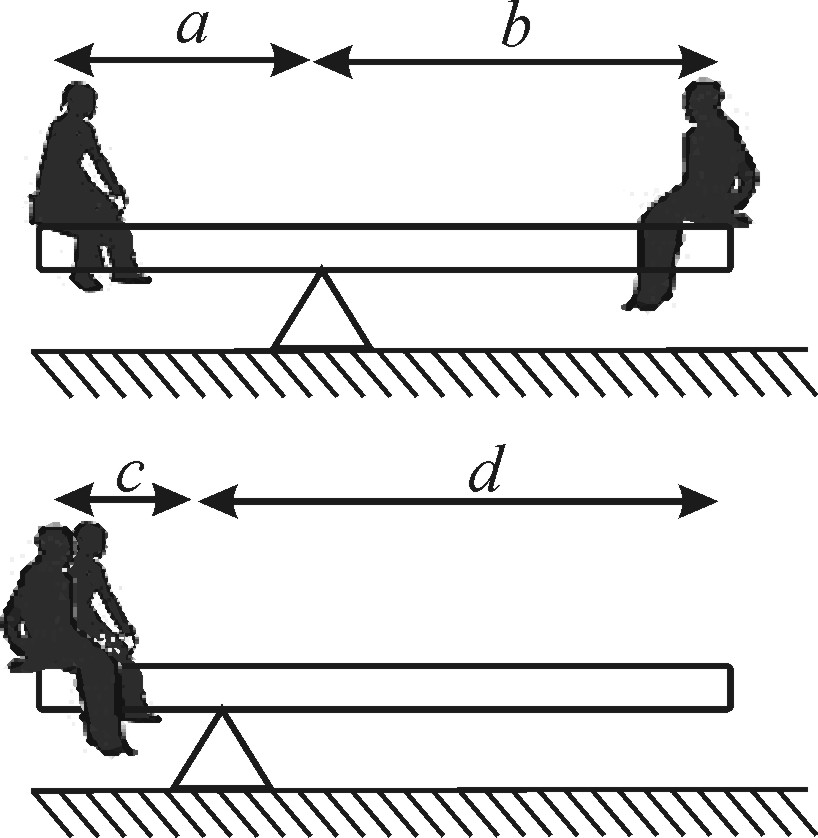 . (10 баллов) Маша и Петя качаются на однородном бревне. Известно, что бревно уравновешено, если Маша сидит на одном, а Петя на другом конце бревна, как показано на верхнем рисунке. Если же подвинуть бревно, и Маша и Петя усядутся на один и тот же его край, то система также будет находится в равновесии, как показано на нижнем рисунке. Бревно имеет длину  метра, в первом случае длина левой части бревна равна  м, во втором случае она составляет  см. Определите, во сколько раз отличаются массы Маши и Пети.

Решение.

Обозначим массу того, кто сидел первоначально слева, через , а массу того, кто сидел справа, . Линейную плотность бревна обозначим (линейная плотность – масса куска бревна единичной длины).

По условию длина левой части бревна  м, а правой  м. Напишем условие равновесия системы, оно же правило рычага:

.

Здесь учтено, что слева на рычаг действует тело весом , имея плечо ; вес куска бревна слева . Масса этого куска распределена, но действует также, как если бы всю ее поместили в центр масс левого куска бревна, поэтому сила имеет плечо . Аналогично определяется правая часть уравнения.

Во втором случае условие равновесия имеет вид:

,

где  м,  м – размеры кусков бревна слева и справа во втором случае.

Сократим оба уравнения на , и перепишем их, сгруппировав с одной стороны, в виде:

, .

Теперь из двух уравнений получим отношение масс. Для этого вынесем за скобки величину :

,

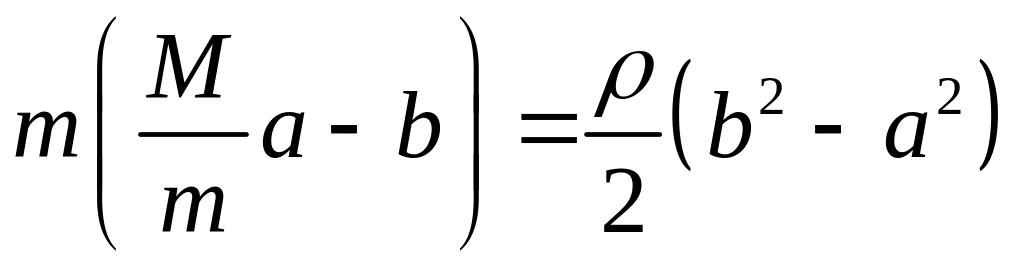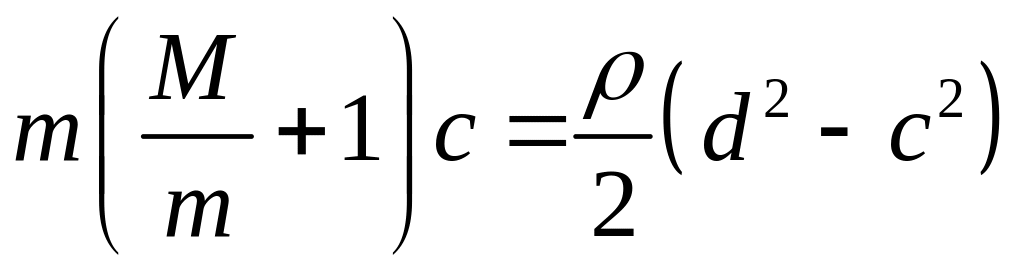
и разделим одно уравнение на другое:

,

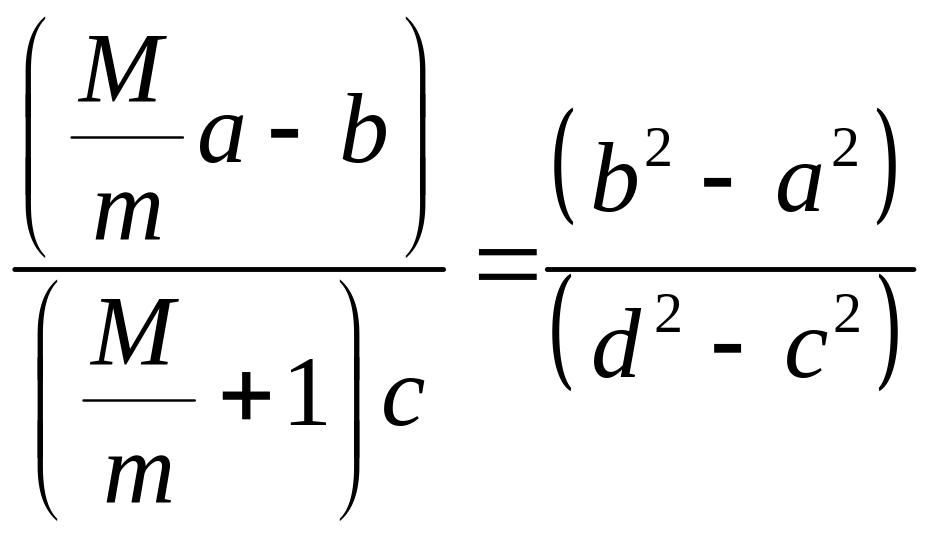или

.

Для упрощения вычислим

.

Отсюда

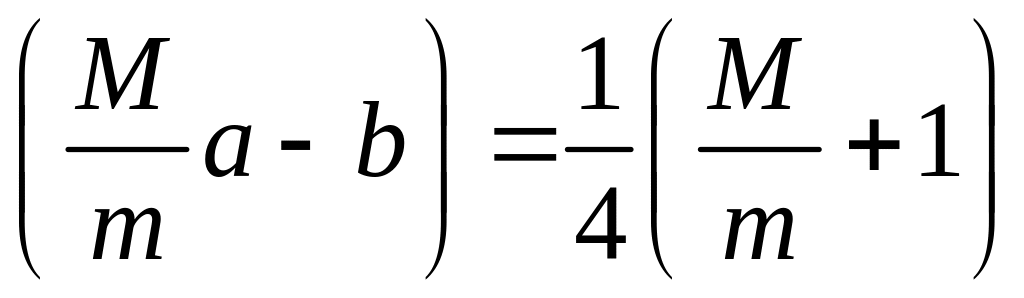или .

Раскрывая скобки, получаем:

.

1. Записано условие равновесия в первом случае – 3 балла.

2. Записано условие равновесия во втором случае – 3 балла.

3. Получен правильный ответ – 4 балла.

3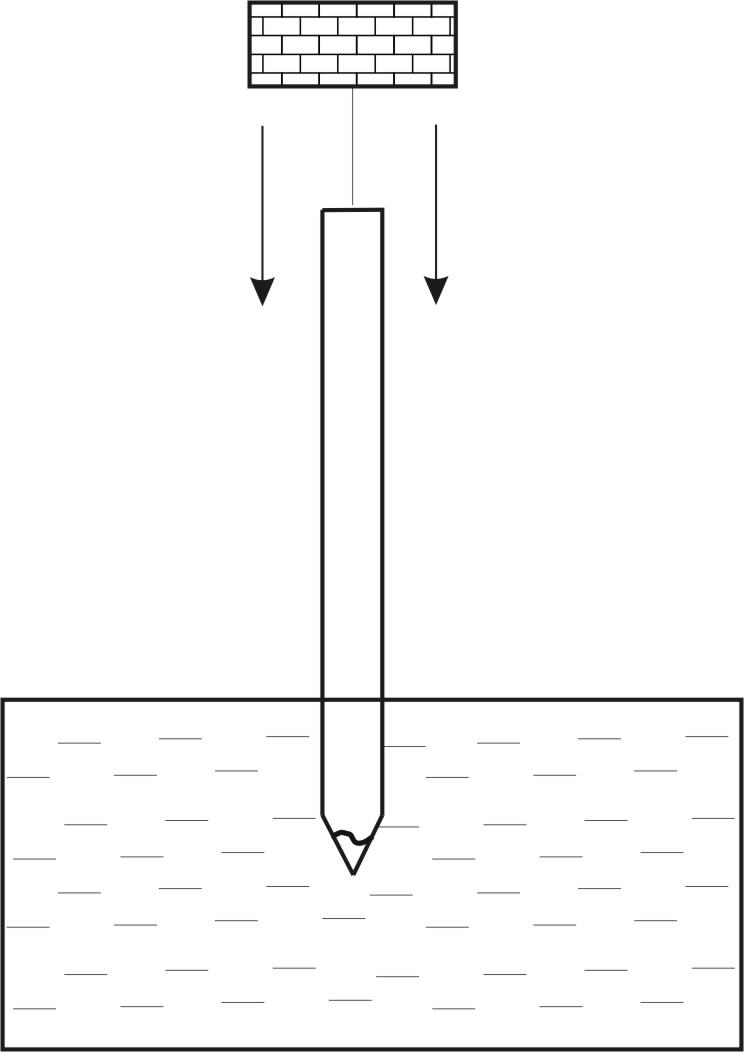 . (10 баллов) Тонкий карандаш, подвешенный на нитке за один из концов, начинают погружать в воду, медленно опуская точку подвеса. Определите максимальную глубину погружения нижнего конца карандаша, если длина карандаша  см, а его средняя плотность в раза меньше плотности воды.