1. Ақпараттық энтропия дегеніміз не?

2. Бүгінгі күнде энтропмяның қандай түрлері белгілі?

3. Шенон бойынша анықтама.

4. Меншікті ақпарат көмегімен анықтау

5. Матиматикалық қасиет

6. Энтропияның тиімділігі

Ақпараттық энтропия —ақпарттың белгісіздік және болжап болмайтын шамасы, бастапқы алфавиттегі қандай да бір нышанның пайда болуының белгііздігі.

Мысалы, орыс тілінде қандай да бір сөйлем құрайтын әріп реттілігі, әр әріп әр түрлі жиілікпен пайда болады, сондықтан кейбір әріптертің пайда болу белгісіздігі басқа әріптерге қарағанда аз.Егер кейбір әріптердің кездесуі сирек еаенін ескерсек, белгісіздік одан сайын азаяды.

Ақпараттық энтропия түсінігін суреттеу үшін Демон Максвелл атын алған термодинамикалық энтропия облысының мысалына жүгінуге болады. Ақпарат және энтропия концепциялары бір-бірімен тығыз байланысқа ие, бірақ бұған қарамастан статикалық механика мен ақпарат теориясындағы теорияның өңделуі көп жылдарға созылды.

Энтропия —статикалық тәуелсіз хабарламаны өндіретін дерекнаманың қарапайым хабарламасына келетін ақпарат көлемі.

Xпен nмүмкін жағдайларындағы тәуелсіз кездейсоқ оқиғалар үшін ақпаратттық екілік энтропия осы формуламен есептеледі

Тек қана «А» әріпінен тұратын, тармақ генерациялаушының қайнар көзінің энтропиясы нөлге тең: , ал мүмкін болар жағдайдың саны:  мүмкін болар жағдай (мәні) («А») логарифм негізіне тәуелді емес.Бұл да ескеретін ақпарат. Энтропиясы нөлге тең, бірақ ақпарат саны 1ге тең разрядты пайдаланатын, есте сақтау құрылғысының мысалы ретінеде, ПЗУ да жазылған әр разряды тек бір ғана мүмкін жағдайға ие, берілгендер разряды бола алады.

Осылай, мысалыға, ағылшын тестінің энропиясы, символға 1,5 бит екенін анықтауға болады және ол әр түрлі тексттер үшін өзгеріп отырады. Берілгендер қайнар көзі энтропиясының дәрежесі берілгендер элементінің битінің ортақ санын білдіреді. Кейбір берілгендер биттерінде ешқандай ақпарат болмауы мүмкін. Мысалыға, әдетте берілгендер структурасы қажет емес ақпаратты сақтап турады, немесе берілгендер структурасындағы ақпаратқа тәуелсіз бірдей секцияға ие.

Энтропия саны әрдайым биттердің бүтін санымен беріле бермейді.

Математикалық әдісі

1. Терістеу  .

2. Шетеулері:  , Йенсен теңсіздігінен вогнутты функция ушін    және  . Егер -тің барлық n элементтері тең болса,   .

3. Егер    тәуелсіз болса, онда  .

4. Энтропия —мүмкін элементтерді орналастырудың томпақ жоғарғы функциясы.

Егер  бірдей элементтердің орналасуына ие болса, онда  .

Нәтижелілік

Алфавит біркелкіден алыс ықтималдықты үйлестіруге ие бола алады. Егер бастапқы алфавит   символдан тұрса, онда оны мүмкін болған анықтауышы біркелкі «оптималданған алфавитпен» салыстыруға болады. Бастапқы және оптималданған алфавит энтропиясының арақатынасы — бұл процентпен берілетін бастапқы алфавиттің нәтижелілігі.   символды бастақы алфавиттің нәтижелілігі -арлы энтропия арқылы анықталуыда мүмкін.

Энтропия шығынсыз теория жүзінде орындалуы мүмкін максималды қысуды шектейді (немесе мүлдем шығынсыз) – әдеттегі теру немесе, практикада, —  Хаффмана,  Лемпеля — Зива — Велча немесе арифметикалық кодтау.

Вариация жәнем жалпылау

B энтропия

Жалпы жағдайда b энтропия ( b тең 2, 3, …) қайнар көзі  бастапқы алфавитімен    және дискретті ықтималдықтарды үлестіру      ықтималдылығы  ( ), формуламен анықталады:

Мысалы :

Тринарлы энтропия

Үшқырлы (b = 3) «чижа» лақтырғанда, тринарлы энтропия қайнар көзі («чижа»)   бастапқы алфавитпен (сандар үшқырдың шегінде «чижа»)   және дискретті біркелкі ықтималдықтарды үйлестірумен (қима «чижа» —теңбағытты үшбұрыш, материал тығыздығы «чижа» барлық объектіге біртекті «чижа»)      ықтималдылығы  ( ) тең:

 трит.

Тетрарлы энтропия

Төртқырлыны (b = 4) «чижа» лақтырғанда, тетрарлы энтропия қайнар көзі («чижа»)   бастапқы алфавитімен (сандар төртқырлының шегінде «чижа»)  және дискретті біркелкі ықтималдықтарды үйлестірумен  (көлденең қима «чижа» — тіктөртбұрыш, материал тығыздығы «чижа» барлық объектіге біртекті «чижа»)      ықтималдылығы  ( ), тең:

 тетрит.

Шартты энтропия

Егер алфавит символдарының ілесімі тәуелді болса (мысалы, француз тілінде «q» аріпінен соң әрдайым «u» әріпі ілеседі, ал «передовик» сөзінен соң газеттерде «производства» немесе «труда» сөздері ілеседі), мундай символдар бірізділігінен туратын ақпарат саны Бірінші шарттың энтропиясы (біріншісі Марков үлгісі үшін бір әріп пайда болу ықтималдығы белгілі ,) деп аталып жатыр (екі әріпті тіркестердің) ықтималдықтары :

Алдыңғы нышаннан тәуелді болатын және — бұл ықтималдық шартта, не алдыңғы нышанмен еді.

Мысалы, « е » [3] әріпсіз тіл орысы үшін.

Дербес және ортақ шартты энтропиялар арқылы осы бөгеттермен каналда берілуде ақпараттық жоғалтулар толық суреттеліп жатыр. Матрица қолданылып жатыр. Тараптармен көз жоғалтулар сипаттама үшін (біресе жіберған сигнал) белгілі бар шартта нышанның қабылдағышпен алудың шартты ықтималдығы қарап жатыр. Бұл каналды матрица келесі түрде болады:

			…		…
			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

Анық, диагональ бойынша орналасқан ықтималдыққа, дұрыс қабылдаудың ықтималдық суреттеп жатыр, ал бағанасының барлығын элементтерінiң сома — қабылдағышқа лайықты нышанның пайда болулар ықтималдығын беріп жатыр. Берілетін сигналға келетін жоғалтуды, дербес шартты энтропия арқылы суреттеледі

Барлығын сигналдарында берілуде жоғалтулар есептеу үшін ортақ шартты энтропия қолданылады :

Тараптармен көздің энтропияны білдіріп , тараптармен қабылдағыштың — энтропия ұқсас қаралып : орнына бәр жерде көрсетіліп жатыр жолдар элементтері (жинақтап алуға болады, ал диагональдар элементтері сол ықтималдық берәләп тұр

Өзара энтропия

Өзара энтропия немесе біріктірулер энтропияы статистикалық тәуелді қатынастар.Энтропия өзара байланысты жүйелер энтропия есеп айырысу үшін арналған және белгі қойып жатыр хабарлағыш мінездейді

Тапсырған және алған сигналдардың өзара байланыс бірлескен оқиғалардың ықтималдықтармен суреттеліп , және канал мінездемелер толық сипаттама үшін тек қана бір матрица керек болады :

		…		…
		…		…
…	…	…	…	…	…
		…		…
…	…	…	…	…	…
		…		…

Канал емес суреттелген кезде, ортағырақ жағдай үшін, ал жүйелер, матрица бүтін өзара жұмыс істе квадрат міндетті емес болуға тиісті. Анық, нөмірімен бағанасының барлығын элементтерінiң сома беріп жатыр, нөмірмен жолдар сомасы бар, ал матрицалары барлығын элементтерінiң сома 1 тең. Оқиғалардың бірлескен ықтималдығы және бастапқы және шартты ықтималдықтар шығарманы сияқты есептеп жатыр :

Байес формуласыбойынша шарт мүмкіндігі орындалады. Осылайша, кабылдау және энтропия қорын есептеуге бүкіл мәліметтер бар.

Өзара энтропия олардың логарифм көбейтіндісі, бүкіл мүмкін матрицаларды жол бойынша (баған ) реттелген қосу арқылы есептеледі.

Өлшеу бірлігі- бит/екі символы,бұл былайша түсіндіріледі, өзара энтропия жұпты символ анықталмағанын суреттейді :анықталған және алынған.

Қарапайым түрлендіру арқылы аламыз:

Өзара энтропия ақпаратты толық мәніне ие – осыдан қарастырылып отырған көлемдерді алуға болады.

Тарихы

1948 жылы, ақпараттың тиімді берілісінің мәселесі арқылы шумдалған коммуникациялық арнаны зерттей келе, Клод Шеннон коммуникацияның түсінушілікке революционерлік мүмкіндіктің тіл табуын ұсынды және энтропиянің бірінші шынай математикалық қағидасын жасады. Оның сенсациялық идеялары екі негізгі бағыттың құрылуына негіз болды, олар: ақпарт теориясы, эгродиялық теорияның және мүмкіндік түсінігін коммуникациялық жүйе және статиқалық мінездеме мәліметтерін қолданады, және кодтау теориясы негізі алгебралық және геометриялық құрылғыны эффективті кодты ұйымдастыру үшін қолданады.

Шеннонмақаласында «A Mathematical Theory of Communication» энтропия түсінігі берілген, екі мақалада жазияланған Bell System Technical Journal 1948 жылы.

Бақылау сұрақтары:

1. Ақпараттық энтропия дегеніміз?

2. Бүгінгі күнде энтропияның қандай түрлері белгілі?

3. Шеннон бойынша анықтау

4. Анықтау өздік ақпарат бойынша

5. Математикалық құрам

6. Энтрапияның тиімділігі

Тақырып 3. Ақпарат көлемі және артықшылық

Лекция мақсаты: Артықшылық түсінігін зерртеу

Сұрақтар:

1. Ақпарат көлемі және энтропия өзара қалай байланысқан?

2. Артықшылық түсінігін анықтау

3. Хабарламадағы ақпарат көлемін анықтау, к тең емес мумкіншілікпен құрылған

4. Дифференциалды энтропияға анықтама беріңіз және оның негізгі сипатын құрастырыңыз

Егер бүкәл анықталмағандық алынса, ақпарат энтропияға тең

І = Н ,

Қарсы жағдайда- бастапқы және соңғы энтропия арасындағы айырмашылық

I=H₁-H₂(3.1)

Ақпараттың көп саны алынады, егер толықтай ең көп белгісіздік түсіріледі - егер барлық оқиғаның мүмкіндіктері бірдей болса.

=Н_макс

_{р - жүзеге асудың мүмкіндін барлық оқиғаның тең мүмкіндігінің арасында. Ақпараттың артығы айырым барынша ықтималдың арасында ақпарат көлемі және энтропияменболады:}

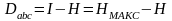(3.2)

Ақпараттың саны сияқты хабарламаның ортақ санының мумкін ұсынысы туындысын к ортаның энтропияснда:

Алғашқы әліпбинің тең мүмкінді және өзара тәуелсіз символ оқиғасы үшін ақпараттың саны арада к m әліпбиінің хабарламаларында тең:

(бит).

Символдық алфавиттегі тең емес ықтималдық этнропиясы :

(бит/символ),

Ақпараттық хабарлама саны, құрастырылған к тең емес ықтималдық символы

Ақпараттар саны келесідей талаптарды қанағаттандырады:

1. Ақпараттар саны екі тәуелсіз хабарламалардың тен қосындылары яғни әрбір ақпараттық сандағы.

2. Жағдайды таңдау мүмкіншілігінің жоғарылауы монотонды қажеттілігі).

3. Шынайы оқиғаларға толы Ақпараттар санының құрамында белгісіздік нолге тең

4. Ақпарат санының тәуелсіздігі хабарламарың сапасынан, әсіресехабарлама алушының маңыздылық дәрежесінен, салдарының мүмкіншілік дәрежесінен және т.б.

Ақпарат желісінің ақпарат жіберу жылдамдығы және өткізгіштік қабілеті

Кедергі жоқ кезде ақпарат беру жылдамдығы ақпарат санымен анықталады, ақпараттың орын ауыстыру символы бірлік уақытқа тең: С =n * H

n –символдық саны , бірлік уақыт кезіндегі хабарлама көзі

Н – хабарлама символын қабылдаған кездегі энтропиясы

Техникалық жылдамдық

V=1/τ (симв/сек),

τ- Екінші ретті алфавиттағы бірдей символдық беру уақыты

Онда, тең ықтималдылықтан құралған хабарлама үшін өзара тәуелсіз ақпараттың беру жылдамдық уақытына тең

С=(1/τ) * log₂ m(бит/сек).

Тең емес ықтималдық жағдайындағы тең символдық уақыты

С= (бит/сек).

Өткізгіштік қасиеті бар жоғары жылдамдықты ақпарат беру төмендігі каналдық желі бойынша

(бит/сек).

Екілік код үшін:

(бит/сек).

Тосқауыл бар болғанда байланыс каналының өткізгіштік қабілеті, хабарлама көзінің энтрапия әртүрлілігі мен шартты энтрапияға секундына келетін nбелгісі санының туындысы арқылы анықталады:

C_n=n*[H(A)-H(A/B)]

немесе

C_n=n*[H(B)-H(B/A)]

Шуылы бар байланыс каналдары арқылы хабарлама жібергендегі ақпараттық жоғалтулар

Қабылдынған хабарламалар ансамбліндегі,ақпараттардың орташа саны

а) бірлескен энтрапия көмегімен:

І(А,В)=Н(А)+Н(В)-Н(А,В) (4,4)

б) шартты энтрапия көмегімен:

І(А,В)=Н(А)-Н(А/В) (4.5)

Айнымалылардың мағыналары:Н(А)- энтрапия,

Н(А/В) – қателіктер әсерінен каналдағы жоғалған ақпарттардың орташа саны.

І(А,В)=I(В,А) (4-6)

(4.4)- (4.5) формулаларынан есептеуге ыңғайлы мына формуланы шығаруға болады:

(4.7)

Дифференциалдық энтропия

Практикада ақпарат көздерінің мүмкін күйлерінің көбісі континиум құрайды, яғни ақпарат көздері үздіксіз.

Үздіксіз ақпарат көзінің энтрпаиясын келесі түрде анықтаймыз:үздіксіз кездейсоқ шаманың өзгеру дипазонын бөлейік U, п соңғы шамасыCu аз интервалында . Cu аз болғандықтан, р(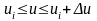 ) ықтималдық реализациясы u мәні u_{i ,} u_i+Cu интервалында:

p( )=

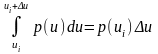
Дискретті кездейсоқ шама U энтрапиясы мына түрде беріледі:

немесе

Өйткені

онда

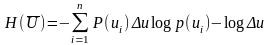
Кемуіне байланысты р ( ), нөлге жақын р( ) ықтималдыққа жақындайды, U дискретті шамасының көлемі - Uүздіксіз кездейсоқшамасына жақындайды . 0 шекке жеткенде үздіксіз энтрапия көзі H(U) үшін келесі теңдікті аламыз :

немесе

(3.4)

Бұл шама 0шексіздікке ұмтылады,толығымен анықтамаға сәйкес келеді, шексіз үлкен саннан тұратын таңдаудың анықталмағандығы шексіз үлкен болдады.

(3.4)қатынасының оң бөлігінің бірінші мүшесі-соңғы мағынасы,U –дың шексіз мүмкін үлкендігін бөлу заңына тәуелді және U кванттау қадамына тәуелсіз.

Осы қатынастың екінші мүшесі U мүмкін үлкендігінің кванттау қадамына ғана тәуелді,H(U)осыдан шексіздікке айналады.

Үздіксіз көзінің ақпараттық ерекшеліктерінің соңғы сипаттамасын алудың бір жолы үздіксіз көзінің анықталмағандығының сапасы ретінде(3.4) қатынасының бірінші мүшесі алынады:

(3.5)

Ол қатыстық дифференциалды энтропия деп немесе жай үздіксіз ақпарат көзінің дифференциалдық энтропиясы деп аталды .Дифференциалдық энтропия ерекшелігі:

a. Егер U –ң мүмкін өлшемінің жалғыз шектеуі оның мүмкін мәндер аймағы болса,онда максималды дифференциалдық энтропия осы аймақтағы мүмкіндікті тең бөлуге ие.

б. Егер U үздіксіз мүмкін өлшемі аймағының шектеуі жоқ болса,бірақ белгілі,дисперсиясы шектеулі,максималды дифференциалдық энтропиясы U өлшемінің дұрыс бөлісуіне ие .

Негізгі әдебиеттер:2[111-119J; 3(109-114]; 9J44-46].

Бақылау сұрақтары:

1.Ақпарат саны және энтропиясы бір-бірімен қалай байланысты?

2. Асқын мағынасын анықтаңыз.

3.к тең емес ықтималды белгілерден тұратын хабарламадағы ақпарат санын анықтаңыз

4. Дифференциалды энтропияға анықтама беріңіз және оның ерекшеліктерін сипаттаңыз

4-тақырып. Сигнал түсінігі және оның модельдері.Детерминделген сигналдардың көрсетілу формалары: уақыттық,жиіліктік,векторлық.

Дәріс мақсаты:

1.Сигнал ұғымы және модельдері

2. Детерминделген сигналдардың көрсетілу формалары

3. Сигналдың уақыттық формасы

Сұрақтар:

1.Детерминді сигнал туралы нені түсінеміз?

2.Детерминді сигналдың математикалық көрсетілім формасының әртүрлілігі

3. Функция жүйесінің ортогональды және ортонорминальды шарттын жазыңыз.

4.Детерминді сингалдың модельдерін зерттеу не үшін қажет?

5.Сингалдың уақыттық көрсетілімін сипаттаңыз.