2. Үздіксіз байланыс каналдарының ақпараттық мінездемесі

Үздіксіз байланыс каналдарының үлгілері. Үзіліссіз сигналдарды жіберуге арналған каналдардарды үздіксіз деп атау қабылданған. Мұндай каналдар әлі күнге дейін телефон байланысының техникасында, радиотаратқышта кеңінен қолданылады.

Нақты үздіксіз каналдар мінездемелері уақыт бойынша кездейсоқ түрде өзгеретін күрделі инерциялық сызықтық емес объектілерді көрсетеді. Мұндай каналдарды талдау үшін әр түрлі қиындық деңгейдегі математикалық модельдер мен нақты каналдарға тең дәрежедегі модельдер жасалынды. Кең таралған модельдер, ол – гаусс каналының көптүрлілігі.

Гаусс каналы деп келесідей құрылған нақты каналдың математикалық моделі түсіндіріледі:

1. Каналдың негізгі физикалық параметрлері детерминирленген шама болып табылады;

2. Каналды өткізу сызығы FK герц жиілігімен шектелген;

3. Каналда аддивтивті ақ шум әрекет етеді – аддитивті флуктуациялық тең жиіліктегі спектрмен шектеулі қуаттағы және амплитуданы орташа таратушы бөгеттер.

Сонымен қатар, канал арқылы тұрақты орташа қуаттылықтағы сигналдар жіберіледі деп болжанады және сигналдар арасында статистикалық байланыс пен шум болмайды, сигнал спектрінің ені мен бөгеттер каналды жібері жолақтарымен шектелген.

Каналдың ақпараттық мінездемесін қарауда (жіберілу жылдамдығы, жіберу мүмкіндігі, қолданылу коэффиценті) негізгі назар гаусс каналына бөлінеді.

Үздіксіз каналдар арқылы ақпарат жіберу жылдамдығы. Үздіксіз каналдар арқылы ақпарат жіберу жылдамдығы – бұл қабылданған үздіксіз сигналдар υ(t) мен соған сай жіберілген u(t) сигналдардың арасындағы уақыт бірлігіндегі орташа ақпарат саны.

Каналды жіберу жолағы үнемі шектелген болғандықтан, үздіксіз хабарламалар жеткілікті уақыт интервалында Т кейбір қателіктермен есеп беру жүйесімен көрсетілуі мүмкін. Корреляциялық байланыстың болуын есептеумен қатар есеп берулер мен соңғы қайталау туралығы арасында бөгеттер әрекет етуі бойынша үздіксіз сигналдардың ақпарат жылдамдығының орташа жылдамдығын Ĩ(VU) аламыз:

Мұнда I(VU) ұқсас өрнек болып саналады (4.25).

Т ұзақтығының көбеюімен байланысты бұл жылдамдық артады, себебі әрбір жаңа есепте жүзеге асырулар нақтыланады. Т→∞ шегінде N-шамалық таратулар аяқталмаған шамалар болады және өрнек (4.27) үздіксіз каналдар арқылы ақпарат жіберу жылдамдығын анықтайды:

Т→∞ шегіне өту барлық мүмкін болатын сигналдар жылдамдығын көрсетеді.

Келуші сигналдардың әр түрлі ансамбльдеріне әсер етуші бөгеттердің зияндылық дәрежесі әр түрлі. Мұның нәтижесінде ақпарат жіберу жылдамдығының мағынасы да әр түрлі.

Үздіксіз байланыс каналдарының өткізу мүмкіндігі. Максималды мүмкін Сн болатын белгілі техникалық мінездемесімен үздіксіз каналдар арқылы ақпарат жіберу жылдамдығы үздіксіз байланыс каналдарының өткізу мүмкіндігі деп аталады:

Мұнда максимумды келуші сигналдардың барлық мүмкін болатын ансамбльдерінен табады.

Ақпаратты беру жылдамдығын гаусс каналы арқылы табамыз:

Гаусс каналы арқылы үздіксіз сигнал uT(t) {uT(t)} ансамблі арқылы орташа Рu қуаттылықпен σ және тең дисперсиямен жіберілсін. Каналдар шығу кезінде {vT(t)} ансамблінен vT(t) сигналын аламыз, ол ξ(t) гаусс бөгетімен бұзылған және орташа қуаттылығы Ρξ(Ρξ = σ ).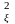

uT(t) сигналының Т ұзақтығы жеткілікті үлкен шама деп аламыз, себебі қателік жіберілген кезде uт(t)-ны νт (t)+ға ауыстыруға болу үшін, және Δt = 1/(2Fк) интервалы арқылы есептеулер, мұнда Fк – каналды өткізу жолағы.

(4.17) өрнегімен сай ақпараттың vT(t) сигналымен жіберілген орташа саны келесі түрде болады:

Мұнда, Н(V) және HU(V) – V кездейсоқ векторының N-шамалы априорлы және апостериорлы энтропиясы, және ол V1, V2, ...,VN кездейсоқ шамалардан тұрады.

Каналдағы бөгеттер аддитивті және келуші сигналдармен статистикалық байланыспаған, олардан келесідей теңдік аламыз:

Н(Ξ) шамасы Ξ бөгетінің кездейсоқ векторының N-шамалы энтропиясын көрсетеді, оның негізін құраушылар Ξ1, Ξ2, ..., ΕΝ кездейсоқ шамалары.

Ақ шумның мағынасын есептей келе есептер моменттері коррелиривті емес және келесідей жазылады:

Мұнда, h(ξ) – бөгеттердің мағынасының бір есептегі дифференциальды энтропиясы.

Орташа таралған және σ дисперсиялы бөгеттер үшін (3.49) болады:

Келуші функциялардың uT(t) есептік мағынасы тәуелсіз деп есептейміз. Оларға тәуелсіз бөгеттер әсері кезінде VT(t) шығушы сигналдардың бөгеттері де тәуелсіз болады.

Сонда H (V) бір есептеулерде дифференциалды энтропия арқылы беріліс сигналын h (V) айқындауға болады :

(4.32) және (4.33) теңдеулері арқылы (4.34) аламыз

Үздіксіз байланыс канал бойынша мәлімет берілу жылдамдығы (4.35) тең

ЕндіГауссканалыныңөткізуқабілеттілігінанықтақтаймыз.

(4.35) өрнекте h(V) максимал мәнін қамтамасыз ететін кіретін сигналдың ансамблін табамыз.

Себебі шығыс сигналдары кіріс сигналдары мен бөгеттердің нәтижелерінің қосындысын көрсетеді, бұл жерде орташа қуат шектелген, кейде шығыс сигналдардың орташа қуаты шектелген. Осындай сигналдар үшін ( § 3.5 қараңыз), ең үлкен мәні h(V) нормальды заң V бойынша бөлу жетіп жатыр. Сонымен қатар белгілі, екі нормальды таралған кездейсоқ шамалардың қосындысы сондай жиынтық дисперсияның бөлу функцияна тең болады. Тек қана нормальды таралған кіріс u сигналында нормальды заң бойынша таралған V болады, не ξ шығыс сигналында нормальды таралған бөгетте бұдан шығып жатыр.

Ал демек, h(V) энтропияның ең үлкен мәндері мен мәліметтер берудің максималды жылдамдықтарының кездейсоқ сигналдарын нормальды ортаға келтірілген жағдайларын қолданады және алады. Сигналдарды орталықтандыруға келтіргенде тапқан орташа қуат қалған дисперсияның максималды мәніне сәйкес келеді.

Оларда сонымен қатар, кең және бірқалыпты энергетикалық спектр алынуы тиіс болғандықтан бұл жағдайда тек қана тәуелсіз есептеулер туралы айтуға болады және (2.23) байланыс қолдану керек.

Канал мүмкіндіктерін көп және толық қолдануы үшін бөгеттерден берілетін сигнал шуыл тәрізді және сол сияқты қасиеттерде болуы тиіс.

Дифференциалды энтропияныңмаксималшама

Гауссканалыныңөткізуқабілеттілігіүшін (4.35) өрнегініңорнына (4.36) қойыпөрнекаламыз:

FK өткізужолағыныңенінгауссканалыныңөткізуқабілеттілігінетәуелдіетіпанықтаймыз.

Сонымен бірге, FK бөгеттердің қуаты сызықты емес тәуелділікпен ықпал етеді, ол (4.37) теңдеуінен шығады. Энергетикалық спектрді бір қалыпты есепке ала отырып шуыл жиілігін Р0 меншікті қуат арқылы оның қуатын Р көрсетеміз.

(4.37) теңдеуі түрінде көрсетіледі

Каналдың өткізу қабілеттілігінің шексіз кеңейтуінің өсу оның өткізу жолақтары СM шекпен шектелген :

Лопиталь ереже бойынша деп белгілеп Сн шегін 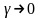дейін анықтаймыз :

тәуелділік сипаттамасын көрсетілген 4.7. суреттегі график арқылы қөрсетуге болады.

Бақылау сұрақтары:

1. Эпсилон түсінігі

2. Үздіксіз хабарлама көздерінің ақпараттық сипаттамасы қандай?

3. Үздіксіз байланыс арналарының акпараттық сипаттамасы қалай бөлінеді?

Тәуелділік сипаттамасын 4.7 суретінде көрсетілген график арқылы анықтауға болады.

Бақылау сұрақтары:

1. Эпсилон туралы түсінік.

2. Үзіліссіз хабарламаның бастауының ақпараттық мінездемелері қандай?

3. Қандай ақпараттық мінездемелер  байланыс үзіліссіз жолымен болады?

Тақырып 10. Тиімді кодтау.  Кедергілерсіз каналадарды кодтау туралы Шеннонның негізгі теоремасы

Дәрістің мақсаты: Тиімді кодтаумен танысу

Сұрақтар:

1. Тиімді кодтау туралы түсінік

2. Шеннон теоремасы

3. Коррелляциясыз тізбекті белгілерді тиімді кодтау әдісі

4.Хаффмен әдісі

Сияқты белгіленді, көбіне хабарламаның белгілеріекіліктің түртіндісініңтізбектілігінде түрленеді. Қара-құрылымдарда сол өзгеріс ескерусіз түс- хабарламаның статистикалық мінездемесі орындалды.

Хабарламаның бастауының статистикалық сипаттарынескере, минимизировать болады түртіндінің ортаныңсанын, үшін хабарламаның бір белгісінің сөйлемшесіүшін сұрайтын, не при болмағандық айғай шудың берілістіңуақытын немесе есінде бол- құрылым көлем азайту.

Кедергілерсіз каналадарды кодтау туралы Шеннонның  негізгі  теоремасы. Кедергілерсіз дискретті канал арқылы тиімді кодтау Шеннон теоремасы арқылы базаланады, оны былай тұжырымдауға болады:

1. Әрбір өндірістің хабарламаның көзі болып оның канал мүмкіндігінің ең азы болып табылады, мынадай шартта:

2. Егер беріліс хабарламасының жинағы щектеусіз болса, онда кодтау тәсілі қолданылмайды.

Дегенмен қатал математикалық дәлеліне қатысты қиын, сондықтан теореманың әділдігі үшін эвристикалық сана сезімге негізделеді.

Айғақтың негізінде ақпараттың берілісініңмжылдамдығының көтермелеуінің мүмкіндігінің идеясынша арнаға жатады, егер  түртіндінің тізбектілігінің кодтауына сәйкесінше жеке белгілерге, және  теорема туралы ола сиптотикалық равновероятности әділ мынадай ұзынды қол тізбектілік. Бұл ретте, табиғи бірінші кезекті кодтау тізбекті болады.

Егер кодтаушы тіззбектің белгілер саны N-ға тең болса, ал энтропия көзі - Н(Z), онда тізбектің саны (4.8) сәйкес келеді.

Ν = Τ/τ, мұндағы Т - кодтық тізбектің ұзындығы, τ - бір белгінің ұзындығы; онда

Әрбір типтік тізбекте соған сәйкес кодтық комбинацияны қою қажет, дәл сондай жалғастырумен Т символмен m алфавит көлемімен. Манипуляция жылдамдығына сәйкес V_T символ саны кодтық комбинацияны TV_Т құрайды.

n_k секілді әртүрлі кодтық комбинация құруға мүмкіндік береді.

(5.7) және (5.8) салыстыру көрсетеді. Соған сәйкес, егер болса, онда канал арқылы жіберілетін кодтық комбинация типтік тізбекті кодтау үшін жеткілікті болады, бірақ кейбір артық кетушіліктер болады.

Типтік емес тізбектіліктерге  арада ұстанымда кодтықәрекеттің сәйкестігіне деген құрулы түртіндінің бірталайүлкен санымен болу біледі. Айыр үшін осы әрекеттерарада түпте және адақта қоса берілген кодтық әрекеттермен үшін тізбектіліктің кодтау типтікпайдаланбаппын артығымнан деген алған. Алайдабарлық типтік емес тізбектіліктерге сәйкестік және біржәне баяғы кодовую әрекетке деген қою боладыкөрсетілген артығымнан, оның дерексіз берілісін жаза.

Дегенмен типтік емес тізбектіліктің бір мүмкіндігі нөлге тырысады, бірінші уақиғада сол ешқандай берілістің тиімділігінде қамтылмайды, ал екіде бас деңгей қабылдау- әрекетінің сенімділігінің ақиқаттық жұқтыр

белгілейміз, нешіншінің мүмкіндіктері типтік тізбектіліктің кодированием шектелетін тең, біз түртіндінің және тәуелсіз түсімін на арнаның кіре берісіне қамсыздандырамыз, бұл артығымның толық жоюына ара жұқтыр хабарламада сәйкеседі.

Шеннон теоремасын қарастырып отырып, былай тұжырымдауға да болады: хабарлама көзі Η(Ζ) энтропиямен m алфавит көлеміндегі тізбекті символдар арқылы да кодтау болады. Бірақ орташа символдар саны l_cр хабарлама санына жақын көлеміне де жуық болуы қажет, бірақ одан аз болмауы қажет.

_{Теоремалар екі бөлігінің әділдігі (m = 2) ұйғарымнен деген тиіс арнаның пропускной зейініне сияқты ақпараттың берілісінің ша барлық көпшілікке бастау тапсырынды сынып ал барынша жылдамдығына берілістің жасау мімкіндігіне нұсқайды. Сол себептен арнаның жіберу зейіні бастаудың кіші өндіргіші, сол хабарламаның жинақтау жағында шарасыз.}