4. Разработка алгоритма обработки сигнала экг: выделение rr интервалов

Для подавления низкочастотного шума необходимо применение ФВЧ, фактически осуществляющего грубую коррекцию изолинии. Для этого достаточно эффективным оказывается применение фильтрации адаптивным средним, осуществляемой следующим образом:

S₁ = x_1/2 , S_n+1=S_n-c(S_n-x_n+1), y_n=x_n-S_n.

где с - адаптивная константа, зависящая от частоты дискретизации y_n=x_n-S_n.

Определить R-зубцы на ЭКГ или соответствующие им зуб­цы на дифференцированной ЭКГ можно с помощью следующего алгоритма. Вычисляется некий порог, и среди значений, которые его превышают, ищется локальный максимум.

Порог может вычисляться, например, как сумма среднего значения ЭКГ и половины максимального значения ЭКГ. Далее ищется первое значение, которое больше порога. От этого значения до первого значения меньшего, чем порог, ищется максимальное значение, которое и определяется как R-зубец.

5. Разработка алгоритма определения времени изгнания по трансторакальной реограмме

1. Получим первую производную трансторакальной реограммы. Для этого воспользуемся алгоритмом цифровой фильтрации, позволяющим совместить в едином алгоритме операции сглаживания и дифференцирования.

Рассмотрим алгоритм, который реализуется нерекурсивным цифровым фильтром. Входная последовательность {x(kT}} ап­проксимируется для каждого из пяти последовательных отсчетов сигнала с абсциссами k = -2, -1, 0, 1, 2 полиномом p₂(t) второго порядка (параболой): P₂(t) = A + Bt + Ct².

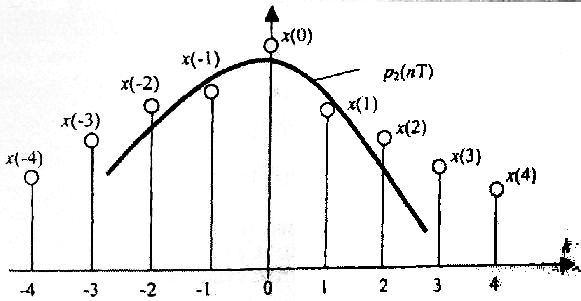
Рисунок 7 - Пятиточечный алгоритм цифровой фильтрации

В качестве выходного значения получаем:

Выходная последовательность при этом подобна входной по­следовательности, но содержит меньше высокочастотных помех, так как параболическая аппроксимация обеспечивает некоторое сглаживание входной последовательности.

Системная функция сгла­живающего фильтра:

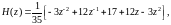
Частотная характеристика такого фильтра имеет вид:

.

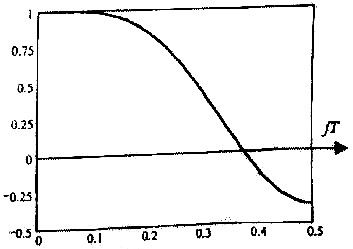
Рисунок 8 - Частотная характеристика сглаживающего цифрового фильтра

Теперь найдем первую производную для функции:

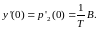
Окончательно по­лучаем:

Системная функция и частотная характеристика используемого нерекурсивного цифрового фильтра будут иметь вид:

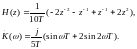
2. Определим момент начала изгнания по дифференцированной реограмме.

Для нахождения точек начала изгнания на графике необходимо рассматривать каждый период в отдельности. Поэтому необходимо разбить график на периодичные части. Точками разделения этих периодов могут служить максимумы дифференцированной реограммы. Их координаты абсцисс заносятся в массив. После нахождения координат происходит анализ реограммы на каждом отдельном периоде.

К кривой дифференцированной реограммы в точке макси­мума второй производной реограммы проводится касательная до пересечения ее с нулевым уровнем. Эта точка является абсциссой точки начала изгнания крови из левого желудочка сердца.

Так как график функции строился по точкам и представляет собой ломанную, то провести касательную к одной точке не представляется возможным. Однако, по определению касательной можно воспользоваться двумя соседними точками и провести через них секущую (касательная является предельным случаем секущей).

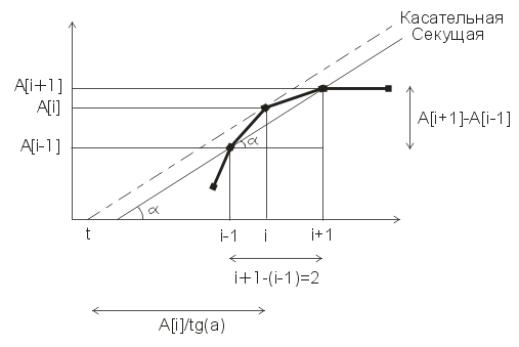
Рисунок 9 - Нахождение производной и её геометрический смысл

Следовательно,

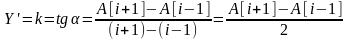
Далее ищется максимальная производная на всем периоде. Абсцисса точки начала выброса определяется через тангенс угла. Чтобы компенсировать сдвиг между секущей и касательной (они параллельны), в формулу будет подставляться координата точки i.

Пусть t – абсцисса точки начала выброса крови. Она равна разности абсциссы точки максимума производной i и основания касательной к точке i.

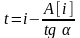, где i – точка максимума второй производной основной реограммы.