Методы многомерной оптимизации

Основные определения.

Рассмотрим следующую задачу

Определение 1.

Поверхностью уровня функции f(x) называется геометрическое место точек, такое что . В случае 2-х переменных поверхность уровня называется линией уровня.

Выделяют три основных типа рельефа поверхности: котловинный, овражный и неупорядоченный.

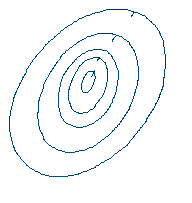
а) котловинный тип рельефа – линии уровня похожи на концентрические эллипсы. В малой окрестности невырожденного минимума рельеф функции котловинный.

б) овражный тип рельефа – линии уровня кусочно-гладкие. Если угол изло-ма направлен в сторону возрастания функции, то геометрическое место точек излома по всем линиям уровня называется истинным оврагом. Если угол излома направлен в сторону убывания функции, то геометрическое место точек излома по всем линиям уровня называется истинным гребнем.

На практике чаще линии уровня всюду гладкие, но на них имеются участки с большой кривизной.

Геометрическое место точек с набольшей крутизной называется разрешимым оврагом или гребнем.

в) неупорядоченный тип рельефа характеризуется наличием многих максимумов, минимумов и седловин. Примером может служить функция имеющая минимумы в точках с координатами и максимумы в точках

Все эффективные методы поиска минимума сводятся к построению траекторий, вдоль которых функция убывает, и отличаются друг от друга способом построения таких траекторий. При этом следует отметить, что метод, приспособленный к одному типу рельефа, может оказаться плохим при другом типе рельефа.

Определение 2.

Градиентом функции многих переменных f(x) называется вектор, составленный из первых частных производных функции по всем переменным:

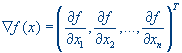
т.е. градиент – это вектор-столбец размерности (n * 1) , где n число перемен-ных функции.

Свойства градиента:

1. Градиент функции перпендикулярен касательной к линии уровня функ-ции f(x)

2. Направление градиента есть направление наиболее быстрого роста функции.

Вектор, противоположный градиенту , называется антиградиентом и направлен в сторону наискорейшего убывания функции. В точке минимума градиент функции равен нулю.

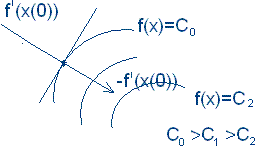
Определение 3.

Матрицей Гессе называется квадратная матрица размерности (n*n), составленная из вторых частных производных функции f(x) по всем переменным

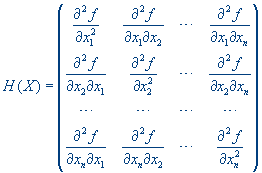
Критерий Сильвестра (критерий знакоопределенности матрицы)

Критерий Сильвестра. Матрица является положительно определенной, если все ее диагональные миноры положительно определены; отрицательно определенной, если они чередуют знак, начиная с «-».

Определение 4.

Точка называется точкой глобального безусловного минимума функции f(x), если при всех . Если при всех то точка называется точкой строго глобального безусловного минимума функции f(x).

Определение 5.

Точкa называется точкой локального безусловного минимума функции f(x), если при всех x лежащих в некоторой окрестности точки . Если неравенство строгое при всех , то точка x* называется точкой строгого локального безусловного минимума функции f(x).

Определение 6.

Точка называется стационарной, если в ней выполнено условие .

Условия экстремума задачи безусловной минимизации.

Теорема1.

(Необходимое условие локальной оптимальности). Пусть - точка локального экстремума f(x), и f(x) дифференцируема в , тогда выполняется условие стационарности .

Не всякая из точек, удовлетворяющих условию стационарности, является точкой экстремума. Она может быть седловой точкой.

В случае функции многих переменных, характер стационарной точки связан со знакоопределенностью матрицы Гессе

Теорема2.

(Достаточное условие локальной оптимальности). Пусть в точке функция f(x) дважды дифференцируема и выполнено условие стационарности . Тогда, если матрица Гессе является положительно (отрицательно) определенной, то точка локального минимума (максимума); если матрица является неопределенной, то седловая точка.

Пример.

Решение.

Градиент функции есть:

Запишем необходимые условия экстремума:

Получена стационарная точка

Для определения характера стационарной точки составим матрицу Гессе:

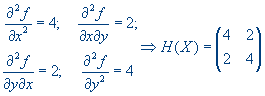
Так как все диагональные миноры матрицы Гессе положительны, то она яв-ляется положительно-определенной матрицей и в соответствии с критерием Сильвестра точка есть точка минимума.

Принципы построения численных методов.

Применение необходимых и достаточных условий безусловного экс-тремума функции многих переменных эффективно при решении ограничен-ного числа задач, в которых вытекающие из условий соотношения имеют аналитическое решение. В большинстве практических ситуациях они не мо-гут быть использованы по следующим причинам:

1. Целевая функция f(x) может не иметь непрерывных производных до второго порядка включительно.

2. Использование необходимых условий сводит решение задачи оптими-зации к решению системы п нелинейных алгебраических уравнений, что представляет собой самостоятельную задачу, трудоемкость реше-ния которой сравнима с трудоемкостью численного решения исходной задачи.

3. Функция, вообще, может быть не задана аналитически.

Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации укладываются в следующую грубую схему. Начиная с некоторого , строится последовательность такая, что

Такие последовательности называются релаксационными, а методы по-строения релаксационных последовательностей — итерационными метода-ми или методами спуска.

Определение 1.

Последовательность называется минимизирующей, если т.е. последовательность сходится к нижней грани f(x).

Определение 2.

Последовательность называется сходящейся к точке минимума, если .

Отметим, что не всякая минимизирующая последовательность является сходящейся.

Пример 1.

Классифицировать последовательность для функции

Решение.

Минимум этой функции достигается в точке .Последовательность для функции является минимизирующей, т.к. , однако она не сходится к точке минимума , т.к.

Пример 2.

Классифицировать последовательность , заданную правилом для функции

Решение.

Минимум этой функции достигается в точке

,

Таким образом, последовательность является и минимизирующей, и сходящейся.

Работоспособность метода еще не гарантирована доказательством схо-димости соответствующей последовательности. Нужна определенная ско-рость сходимости.

Рассмотрим последовательность сходящуюся к точке минимума . Будем предполагать, что все элементы последовательности различны и не совпадают с .

Определение 3.

Последовательность называется сходящейся с порядком r, если r – максимальное число, для которого

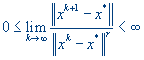
При r =1 говорят о линейной скорости сходимости или о сходимости со скоростью геометрической прогрессии, что может быть представлено в виде неравенства для достаточно больших k

,

где а при говорят о сверхлинейной скорости сходимости. При r=2 говорят о квадратичной скорости сходимости

Пример 1.

Определить порядок сходимости последовательности , где

Решение.

Каждый следующий член этой последовательности равен квадрату предыдущего, а ее предел равен нулю. В соответствии с определением имеем

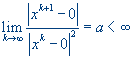
поэтому сходимость квадратическая.

Пример 2.

Определить порядок сходимости последовательности , где

Решение.

Каждый следующий член этой последовательности равен квадратным корнем предыдущего, а ее предел при любом a > 0 равен единице. В соответствии с определением имеем 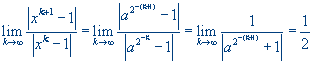, поэтому сходимость линейная.

Пример 3.

Определить порядок сходимости последовательности , где k=0,1,2,… .

Решение.

Последовательность сходится к

, поэтому сходимость линейная.

Пример 4.

Определить порядок сходимости последовательности , где k=1,2,… .

Решение.

Последовательность сходится к

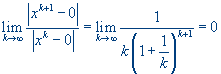
Т.к. r=1 и c=0, то сходимость сверхлинейная.

Классы функций.

Особенно легко вопросы существования и единственности решаются для выпуклых функций. Эти функции являются очень важным объектом в теории оптимизационных задач. Введем ряд определений.

Определение 1.

Функция f(x), называется выпуклой, если при всех

Если неравенство строгое, то f называется строго выпуклой.

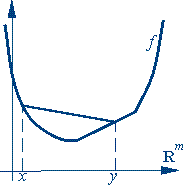
Геометрически выпуклость означает, что график функции на интервале (x, y), соединяющем любые точки x и y, лежит не выше прямой, соединяющей точки (x, f(x)) и (y, f(y)).

Определение 2.

Функция f(x),определенная на называется называется сильно выпуклой с константой l > 0, если при всех

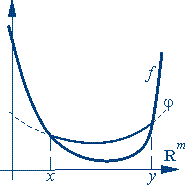
Геометрически это понятие можно интерпретировать так.

Пусть точки отрезка [x, y], соединяющего точки x и y, параметризованы параметром . Правая часть неравенства определяет на этом отрезке полином второго порядка (от ).График сильно выпуклой функции над отрезком [x, y] должен лежать ниже параболы — графика этого полинома.

Для дифференцируемой функции f(x), выпуклость эквивалентна неравенству

или

строгая выпуклость – неравенству

или

сильная выпуклость – неравенству

или

или

Для дифференцируемой сильно выпуклой функции f(x) точка минимума существует, единственна и

Классификация методов.

Детерминированные алгоритмы безусловной минимизации делят на классы в зависимости от вида используемой информации для формирования направления перехода. Если на каждой итерации используются лишь значения минимизируемых функций, то метод называется методом нулевого порядка. Если, кроме того, требуется вычисление первых производных минимизируемой функции, то имеют место методы первого порядка, при необходимости дополнительного вычисления вторых производных - методы второго порядка.

Общая характеристика методов нулевого порядка.

В этих методах для определения направления спуска не требуется вычислять производные целевой функции. Направление минимизации в данном случае полностью определяется последовательными вычислениями значений функции, и сводятся к построению траектории спуска , вдоль которой целевая функция убывает:

Общая характеристика методов первого порядка.

Методы первого порядка основаны на свойствах градиента, поэтому они также называются градиентными методами минимизации. Использование этих методов в общем случае позволяет определить точку локального минимума функции.

В градиентных методах, если нет дополнительной информации, то из начальной точки разумно перейти в точку , лежащую в направлении антиградиента - наискорейшего убывания функции. Выбирая в качестве направления спуска антиградиент – в точке , получаем итерационный процесс вида

В координатной форме этот процесс записывается следующим образом:

i = 1, ..., n; k= 0, 1, 2,...

В качестве критерия останова итерационного процесса используют либо выполнение условия малости приращения аргумента , либо выполнение условия малости градиента , где в качестве нормы берется евклидово расстояние.

Возможен и комбинированный критерий, состоящий в одновременном выполнении указанных условий.

Геометрическая интерпретация метода.

Градиентные методы отличаются друг от друга способами выбора ве-личины шага