Основные законы алгебры логики и формы логических функций

Основные законы устанавливают эквивалентность логических формул, образованных с помощью функций первой полной системы и позволяют приводить исходные логические функции к виду, удобному для дальнейшего использования. К этим законам относятся

• Переместительный (коммутативности) закон для дизъюнкции:

• Переместительный (коммутативности) закон для конъюнкции:

• Сочетательный (ассоциативности) закон для дизъюнкции:

• Сочетательный (ассоциативности) закон для конъюнкции:

• Первый распределительный (дистрибутивный) закон:

• Второй распределительный (дистрибутивный) закон:

Приведенные выше законы, за исключением последнего, полностью аналогичны соответствующим одноименным законам алгебры. Последний же алгебраических аналогов не имеет, поэтому рассмотрим его отдельно (таб. 13).

Таблица 13. Таблица истинности второго дистрибутивного закона

Из приведенной таблицы видно, что закон действительно имеет место. Следующие два закона также не имеют алгебраических аналогов.

• Закон инверсии для дизъюнкции: отрицание дизъюнкции двух логиче­ских переменных равносильно конъюнкции их отрицаний

Рассмотрим таблицу истинности для функции

Операция	Значения переменной

Таблица 13. Таблица истинности второго дистрибутивного закона

что и требовалось доказать. Закон справедлив и для произвольного числа логических переменных, т.е.

• Закон инверсии для конъюнкции: отрицание конъюнкции двух логиче­ских переменных равносильно дизъюнкции их отрицаний

В этом случае таблица истинности имеет вид:

Операция	Значения переменной

Имеет место обобщение закона для произвольного числа логических переменных, то есть

Используя законы алгебры логики можно упрощать сложные логические функции. При этом часто используются следующие тождества и , где — любая сложная логическая формула (функция). Тогда если дизъюнкция логических переменных (формул) содержит хотя бы одну пару слагаемых, из которых одно есть некоторая переменная (формула), а другое — ее отрицание, то она является тождественно истинной, то есть .

Если конъюнкция логических переменных (формул) содержит хотя бы одну пару множимых, из которых одно есть некоторая переменная (формула), а другое — ее отрицание, то она является тождественно ложной, то есть

Заметим, что любая логическая функция может быть выражена различными формулами, которые являются эквивалентными, что следует из возможности проведения эквивалентных преобразований. На практике часто используют так называемые нормальные формы представления сложных логических функций. При построении этих форм пользуются некоторыми понятиями, основными из которых являются понятия элементарной конъюнкции и элементарной дизъюнкции.

Элементарной конъюнкцией Q называется логическое произведение пе­ременных и (или) их отрицаний, причем каждая переменная (ее отрицание) в произведении должна встречаться только один раз например,

Число переменных, составляющих элементарную конъюнкцию, называется ее рангом, то есть если конъюнкция имеет ранг равный , то она составляется из логических переменных. Конъюнкции, тождественно эквивалентные единице, считаются элементарными конъюнкциями нулевого ранга.

Аналогично вводится понятие элементарной дизъюнкции. Элементарной дизъюнкцией называется логическая сумма инверсированных или не инверсированных переменных, причем каждая переменная встречается в сумме только один раз. К элементарным относится, например, дизъюнкция

Используя введенные понятия элементарной конъюнкции и элементарной дизъюнкции, дадим определения дизъюнктивной и конъюнктивной нормальным формам. Итак, формула, эквивалентная данной формуле и представляющая собой логическую сумму элементарных конъюнкций, называется дизъюнктивной нормальной формой (д. н. ф.) данной формулы, или дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой. Для логических функций это означает следующее: логическая функция задана своей дизъюнктивной нормальной формой, если она выражена посредством логической суммы элементарных конъюнкций, Дизъюнктивная нормальная форма существует для любой формулы алгебры логики, то есть для любой логической функции.

Конъюнктивная нормальная форма (к. н. ф.) вводится аналогично дизъюнктивной нормальной форме. Считается, что логическая функция задана своей конъюнктивной нормальной формой, если она выражена посредством логического произведения элементарных дизъюнкций. Конъюнктивная нормальная форма подобно д. н. ф. существует для любой формулы алгебры логики, то есть и для любой логической функции.

Одна и та же логическая функция путем эквивалентных преобразований может быть представлена различными дизъюнктивными или конъюнктивными нормальными формами. Из множества нормальных форм, представляющих данную функцию, выде­ляют одну дизъюнктивную и одну конъюнктивную форму такого типа, что каждая не тождественно ложная (для случая д. н. ф.) или не тождественно истинная (для случая к. н. ф.) функция представляется единственным образом. Такие нормальные формы по­лучили наименование совершенных. Возможность и единственность представления любой функции алгебры логики в виде совершенных нормальных форм вытекает из положений о разложении произвольных логических функций при использовании только дизъюнкций, конъюнкций и логических отрицаний.

Совершенной дизъюнктивной нормальной формой логической функции от различных двоичных переменных называется д. н. ф., обладающая следующими свойствами [4]:

• в ней нет двух одинаковых конъюнкций;

• ни одна конъюнкция не содержит двух одинаковых двоичных пере­менных;

• никакая конъюнкция не содержит двоичной переменной вме­сте с ее отрицанием;

• все конъюнкции имеют ранг , причем каждая из них содержит либо переменную либо ее отрицание

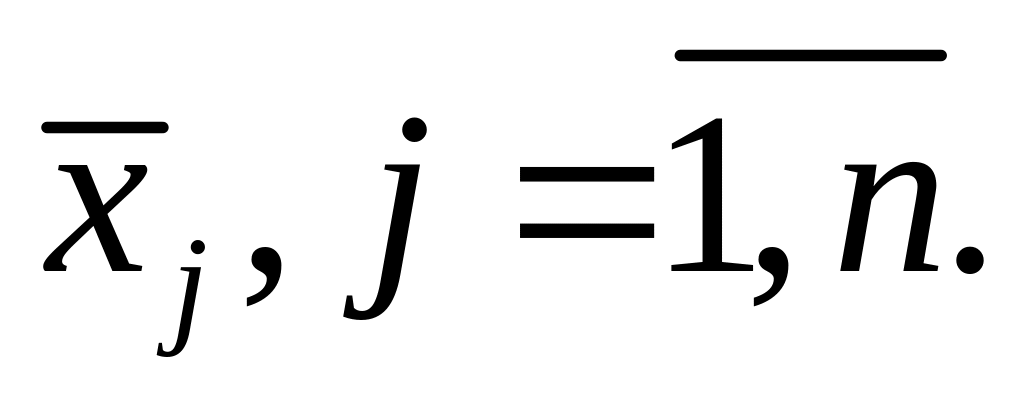
Данные свойства можно использовать для приведения любой не тождественно ложной функции к совершенной дизъюнктивной нормальной форме. Произвольная логическая функция приводится к совершенной д. н. ф. в такой по­следовательности :

• функция приводится к какой-либо дизъюнктивной нор­мальной форме; выполняется условие D — конъюнкции, не содержащие всех переменных, дополняются до их полного числа с получением конъюнкций только ранга 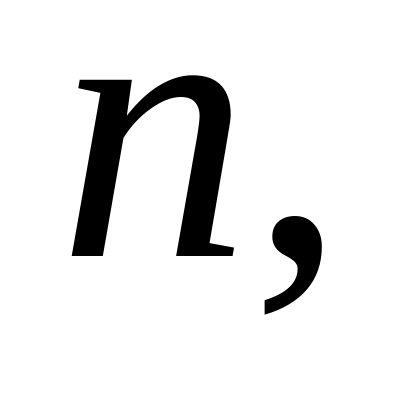для чего используются соотношения типа

• из полученной д. н. ф. с конъюнкциями ранга удаляются конъюнкции тождественно ложные и лишние, то есть повторяющие другие конъюнкции.

Рассмотрим следующий пример [4]:

Привести функцию к совершенной д. н. ф.

Используя приведенную выше формулу, получим, что

.

Первая и третья конъюнкции идентичны. Исключение одной из них не влияет на истинность конечного результата. Действительно, для любой логической функции справедливо равенство , и окончательный результат имеет вид

Совершенная конъюнктивная нормальная форма строится аналогично совершенной д. н. ф. Совершенной к. н. ф. логической функции от двоичных переменных называется конъюнктивная нормальная форма, удовлетворяющая следующим условиям [4]:

• в ней нет двух одинаковых дизъюнкций;

• ни одна дизъюнкция не содержит двух одинаковых двоичных пере­менных;

• ни одна дизъюнкция не содержит какой-либо двоичной пе­ременной вместе с ее отрицанием;

• каждая дизъюнкция содержит в качестве слагаемого либо двоичную переменную либо ее отрицание