1.2 Характеристики выборки

1. Размах. Размахом, r, (вариационным размахом) называется разность между наибольшими и наименьшими значениями х_i в выборке:

r = M_i (max) - х_i (min) (1.2)

2. Мода. Значение х_i, соответствующее максимуму в распределении выборки (значение х_i, частота которого наибольшая).

3. Медиана. Медианой, m, называется такое среднее значение х_m, которое делит ранжированную совокупность значений х_i на две равные по количеству х_i части. В одной части х_i  х_m , а в другой х_i < х_m. При четных значениях n: x_m= (x_n/2 + x_n/2+1)/2 (1.3)

При нечетных значениях n: x_m = x_{(n+1) / 2} (1.4)

4. Средние величины. При обработке результатов экспериментальных наблюдений большое значение имеют средние величины, , способные при замене случайных величин х_i не изменять свойства выборки или генеральной совокупности.

Если n_i - количество оценок, приводящих к значению х_i, а w_i - их весовая доля, причем n_i= w_i / х_i, то средние значения могут быть оценены из формулы

= , (1.5)

где а - степень усреднения;

1) а=0 -среднее или среднечисленное значение средней;

2) а=1 - средневзвешенное или средневесовое значение средней;

3) а=2 - более сложные случаи усреднения, применяются, например, для оценки средних молекулярных масс полимеров.

Примером вычисления является оценка средних размеров смеси частиц различного диаметра, D. Средним вероятным диаметром частицы является величина D, оцениваемая как медиана: половина частиц имеет больший, чем D, диаметр, половина − меньший. Если текущий диаметр D_i, то:

средний арифметический диаметр: , (1.6)

где n-число частиц,

средний геометрический размер: (1.7)

Существуют и другие виды средних.

Величина (х_i - ) называется отклонением х_i от средней арифметической, причем (x_i- ) = 0. Степень рассеяния случайных величин относительно средней арифметической характеризуется дисперсией (² - для генеральной совокупности, s²- для выборки):

 ² = (1.8)

Положительное значение квадратного корня из дисперсии называется средним квадратичным отклонением или стандартом и является оценкой экспериментальной ошибки:

 = (1.9)

Правило трех сигм. Практически все ошибки измерений заключены между минус 3 и плюс 3. Ошибки,  , большие, чем 3, встречаются лишь в трех случаях из 1000.  = 3  называется наибольшей возможной ошибкой измерения.

1.3 Характеристика распределений случайных величин

1.3.1 Нормальное (гауссово) распределение описывается уравнением:

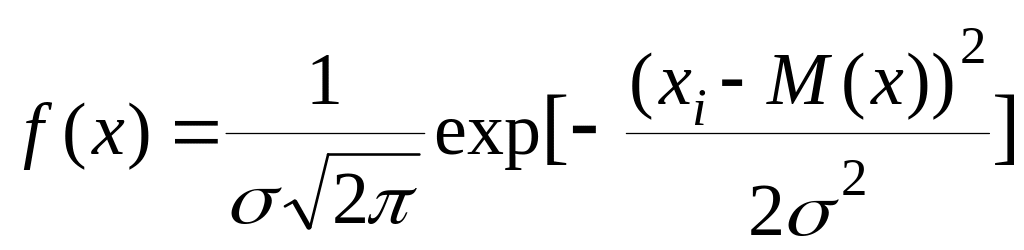(1.10)

Если х_i можно рассматривать как результат суммарного воздействия многих независимых факторов, то закон распределения такой случайной величины близок к нормальному.

Гауссово распределение является предельным законом, к которому приближаются другие законы распределения случайных величин при определенных условиях. Такое распределение играет фундаментальную роль в теории ошибок, так как:

 оно описывает распределение ошибок, обусловленное множеством малых независимых воздействий, носящих случайный характер;

 многие функции случайных величин, такие как ,  ² и другие, распределены асимптотически нормально даже в тех случаях, когда исходная величина не следует нормальному закону.

1.3.2 Критерий согласия (критерий Пирсона). Критерий Пирсона ( -критерий) является мерой расхождения между фактической, Ф, и теоретической, Е, частотой случайных причин появления некоторого события.

Если х_i - независимое распределение случайной величины со средним, равным нулю, и среднеквадратичным отклонением, равным 1, то сумма квадратов этих величин = подчиняется распределению с f степенями свободы. В лабораторной и технологической практике часто приходится встречаться с задачами такого рода. Определение какого-то свойства (прочности, удлинения нити и пр.) проводится несколько раз, причем известна теоретическая частота, Е, появления некоторого события при этом испытании. Вместе с тем, на практике фактическая частота Ф отличается от Е.

Можно ли объяснить это расхождение случайными причинами? Например, в производстве вискозной текстильной нити сменяемость фильер на формовочной машине составляет 13,6 на 1000 “фильерочасов”. В результате проведенных работ по оптимизации технологического процесса сменяемость фильер снизилась до 5,7. Можно ли эту разницу в сменяемости фильер объяснить случайными причинами или же она обусловлена улучшением технологического режима? Разница между теоретической (исходной), Е, и фактической частотами, Ф, сменяемости называют критерием значимости. Критерии значимости  это случайная величина, распределение которой представляет собой специально подобранную функцию, зависящую только от числа опытов (числа степеней свободы). Критерий значимости обычно выбирают таким, чтобы вероятность p отвергнуть гипотезу была малой, когда гипотеза верна. Если p окажется малой величиной, значит, мала вероятность того, что в силу случайных причин критерий значимости примет экспериментальное значение. Поэтому критерий значимости в этом случае достигает своего значения не в силу случайных величин, а (Ф-Е) существенно.

Если р окажется не очень малой величиной, то значение (Ф-Е)  случайная величина. Вопрос о том, мала или значительна величина p, зависит от характера рассматриваемой задачи.

Результаты математической обработки экспериментальных данных позволяют сформулировать некоторую гипотезу (статистическую гипотезу) о причинах обрывности нити при формовании. Статистической гипотезой, Н, называется любое предложение о свойствах генеральной совокупности, из которой делается выборка. Различают исходную (Н₁) и конкурирующую (Н₂) гипотезы. Существуют две опасности в выборе “Н”: отвергнуть Н₁, когда она справедлива, т.е. допустить, что она не соответствует опытным данным, хотя в действительности Н₁ справедлива. Это так называемая ошибка I рода. Ошибкой II рода называют принятие неверной гипотезы. Вероятность ошибки I рода, p₁, называется уровнем значимости. Вероятность правильного исхода недопущения ошибки I рода, , называется доверительной вероятностью:

 =1-р 1.11)

Обычно для технологических экспериментов принимают уровень значимости 0,05, т.е. доверительную вероятность 0,95 (95%).

Определим вероятность того, что из-за случайных воздействий критерий значимости примет значения, равные или большие экспериментальных значений. Если эта вероятность окажется малой, то это означает, что возможность достижения критерием значимости экспериментальных величин маловероятна. Если же эта вероятность достаточно велика, то расхождение между теоретической и фактической частотами оказывается случайным.

Для оценки значимости разницы частоты появления некоторого события от ожидаемого значения х_i применяют критерий согласия ( -критерий):

= , (1.12)

где - фактически полученное значение частоты;

- ожидаемая частота, причем >5;

- критерий характеризует правомочность выбора той или иной гипотезы.

Таблица функций (приложение А, таблица А.1) составлена по двум аргументам: одним из них является доверительная вероятность, p, а другим - число степеней свободы f = n-1. Обычно значение доверительной вероятности р выбирается равным 0,95, т.е. 95%. Если вычисленное значение превысит табличные значения (см. приложение А, таблица А.1) , то из этого следует, что данная выборка характеризуется распределением, существенно отличающимся от гипотетического распределения. Поэтому гипотезу следует отвергнуть. В противном случае ( < ) гипотеза принимается.

Например, анализ статистических результатов, полученных при работах по улучшению качества вискозной текстильной нити, показывает, что < . В этом случае можно утверждать, что уменьшение обрывности нити при формовании достигнуто не в силу случайных воздействий, а целенаправленно.

Пример. Прочность волокон и нитей определяется с помощью разрывных машин, динамометров.

В одной серии измерений было испытано 10 образцов нитей, причем 5 из них разрывалось при нагрузке меньшей, чем предусмотрено нормативами. В другой серии измерений испытывалось 20 образцов, и 14 из них также не выдержало испытаний. Можно ли считать, что прочность нитей определяется различиями в их структуре или же различие в результатах опытов объясняется случайными причинами?

Всего испытанию подвергалось 20+10=30 образцов нитей. Из них не соответствует нормативным характеристикам 5+14=19. Следовательно, вероятность того, что случайно выбранный образец нити окажется не соответствующим нормативным характеристикам, равна 19/30. Поэтому, теоретическое число бракованных нитей в первой серии опытов равно р₁=(19/30)10 = 6,33, а во второй р₂=(19/30)20=12,66. Теоретическое число качественных нитей: р₁=(11/30)10=3,66 и р₂=(11/30)20=7,33. Поэтому:

=

Число степеней свободы f = 2-1 = 1. В соответствии с таблицей А.1 приложения А, вероятность гипотезы p=0,29. Так как значение p не мало, то нельзя утверждать, что различия определяются различной структурой нити.