
- •Теоретична частина
- •Приклад 2. Знайти загальний розв’язок рівняння
- •Практична частина
- •Кривуца в.Г., Барковський в.В., Барковська н.В.Вища математика. Київ, цул, 2003.
- •Литвин і.І., Конончук о.М., Желєзняк г.О. Вища математика. Київ, цул, 2004.
- •Богомолов м.Н. Практичні заняття з математики. Київ, Вища школа, 1986.] Теоретична частина
- •Практична частина
- •Кривуца в.Г., Барковський в.В., Барковська н.В.Вища математика. Київ, цул, 2003.
- •Литвин і.І., Конончук о.М., Желєзняк г.О. Вища математика. Київ, цул, 2004.
- •Богомолов м.Н. Практичні заняття з математики. Київ, Вища школа, 1986.] Теоретична частина
- •Для визначення часткового розв’язку спочатку знайдемо похідну у функції
- •Практична частина
Державний університет телекомунікацій
Навчально-науковий виробничий центр, м. Львів
Затверджую
Зав. ННВЦ
__________ Яковлєва Т.С.
“___” _______ 2014 р.
Практична робота №1
Диференціальні рівняння
з дисципліни “Вища математика”
для студентів заочної, прискореної форми навчання
(ІІІ курс, V семестр)
Склав: доцент, к.ф.-м.н.
Плешівський Я.М.
м.Львів-2014 р.
Тема: Розв’язування диференціальних рівнянь І порядку з роздільними та подільними змінними і однорідних
Мета: Навчитись розв’язувати диференціальних рівнянь з роздільними змінними і однорідних
Література:
Кривуца В.Г., Барковський В.В., Барковська Н.В.Вища математика. Київ, ЦУЛ, 2003.
Литвин І.І., Конончук О.М., Желєзняк Г.О. Вища математика. Київ, ЦУЛ, 2004.
Богомолов М.Н. Практичні заняття з математики. Київ, Вища школа, 1986.]
Теоретична частина
Диференціальним рівнянням n-го порядку називають вираз F(x, y, y, y...y(n)) = 0, де х- незалежна змінна, у- невідома функція, у , у,..., y(n) - похідні невідомої функції.
Розв’язком диференціального рівняння називають будь-яку функцію, яка при підстановці її в рівняння перетворює його в тотожність.
Порядком диференціального рівняння називають порядок найстаршої похідної, яка входить в це рівняння.
Загальним розв’язком (загальним інтегралом) диференціального рівняння називають таку функцію, яка перетворює дане рівняння в тотожність і містить стільки незалежних довільних сталих, який порядок цього рівняння.
Початковими умовами називають значення функції та її похідних в заданій точці х0.
Розв’язок диференціального рівняння, який задовільняє заданим початковим умовам називають частковим розв’язком, а задачу знаходження часткового розв’язку - задачею Коші.
Загальний вигляд диференціального рівняння І порядку з роздільними змінними наступний:
Х(х)V(y)dx+X1(x)V1(y)dy = 0,
де Х(х), Х1(х) функції тільки від х; V(y), V1(y) - функції тільки від у.
Поділивши обидві частини рівняння на добуток Х1(х) V(y), отримаємо рівняння з відокремленими змінними:
![]() .
.
Загальний інтеграл цього рівняння має вигляд:
![]() .
.
Приклад 1
Розв’язати рівняння (1+ех)уу = ех.
Знайти частковий розв’язок при умові: у = 1, якщо х = 0.
Розв’язання:
Оскільки
![]() то
то
![]() звідси
звідси
(1+ех)ydy
= exdx,
![]()
![]() .
.
Після
потенціювання отримаємо:
![]()
Підставимо
в загальний розв’язок у=1
і х=0.
Отримаємо
![]() .
Звідси
.
Звідси
![]() .
Отже, частковий розв’язок рівняння при
наших умовах має вигляд:
.
Отже, частковий розв’язок рівняння при
наших умовах має вигляд:
![]() ,
або
,
або
![]() .
.
Однорідним диференціальним рівнянням першого порядку називають рівняння, яке можна записати у вигляді
![]() або
або
![]()
де
функції
![]() не
змінюються при заміні x
на tx, тобто
не
змінюються при заміні x
на tx, тобто
![]() .
.
Для
розв’язання такого рівняння використовують
заміну
![]() ,
в результаті якої одержують рівняння
з роздільними змінними.
,
в результаті якої одержують рівняння
з роздільними змінними.
Приклад 2. Знайти загальний розв’язок рівняння
Розв’язання
Запишемо дане рівняння у вигляді
 .
Тому, що права частина рівняння ( функція
.
Тому, що права частина рівняння ( функція
![]() )
така, що
)
така, що
![]() дане рівняння є однорідним. Введемо
заміну
і одержимо
дане рівняння є однорідним. Введемо
заміну
і одержимо
 ,
тобто рівняння з роздільними змінними.
,
тобто рівняння з роздільними змінними.
Інтегруючи праву та ліву частини рівняння одержимо
![]()
(
Інтеграл в лівій частині взяли заміною
![]() ).
Функція
).
Функція
![]() ,
отже
,
отже
![]() -
загальний розв’язок заданого рівняння.
В явному вигляді (розв’язано відносно
у )
знайдений розв’язок матиме вигляд
-
загальний розв’язок заданого рівняння.
В явному вигляді (розв’язано відносно
у )
знайдений розв’язок матиме вигляд
![]() .
.
Практична частина
Знайти розв’язок задачі Коші для диференціальних рівнянь І-го порядку з роздільними змінними
 y(0)
= 2
y(0)
= 2

 ,
, 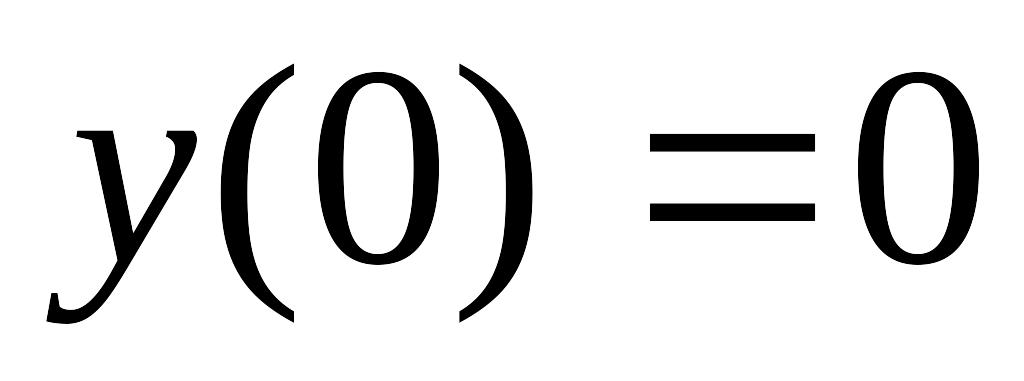
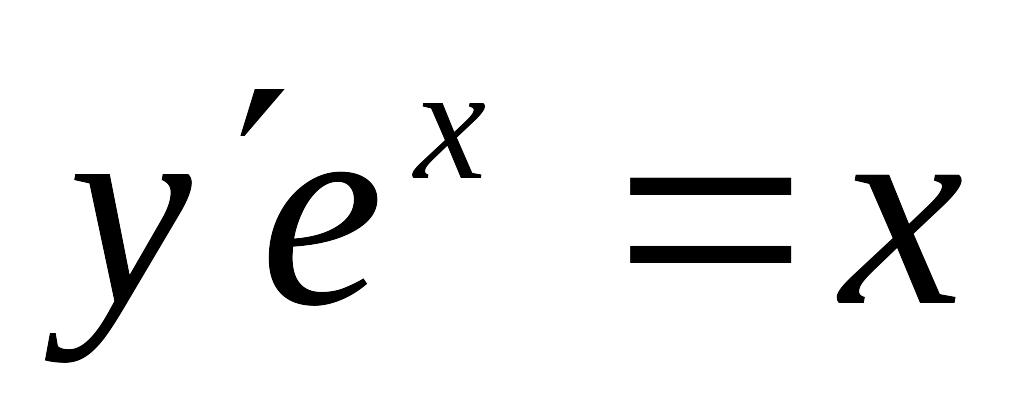 ,
, 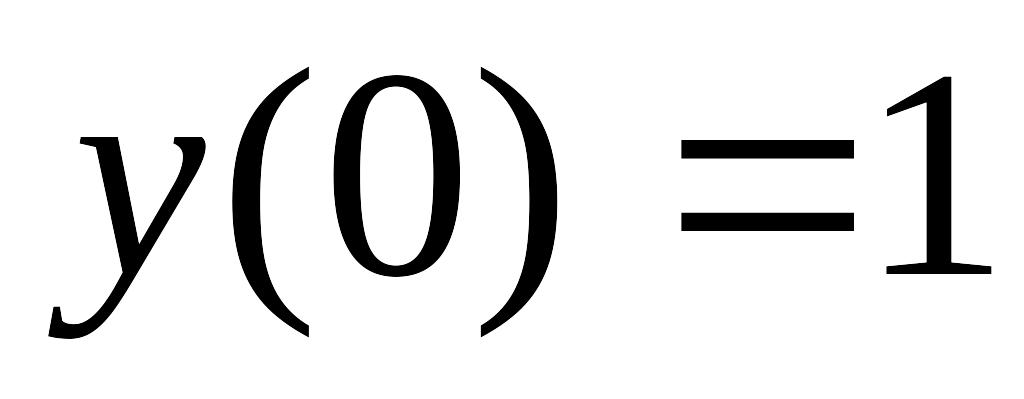

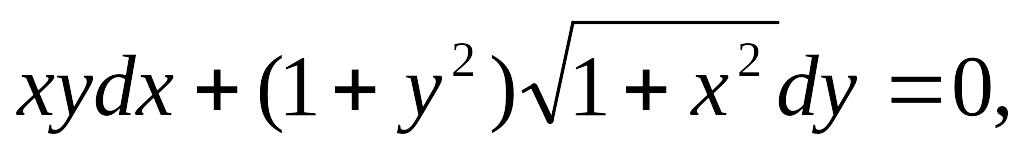
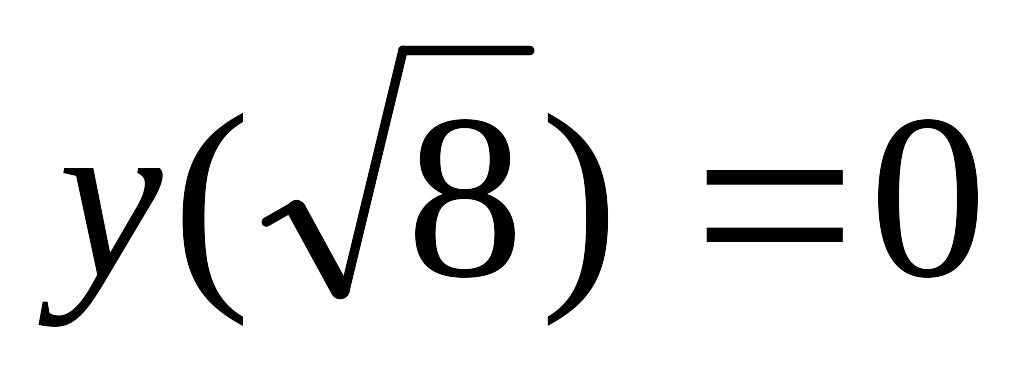
 , y(0)
= 1
, y(0)
= 1
,
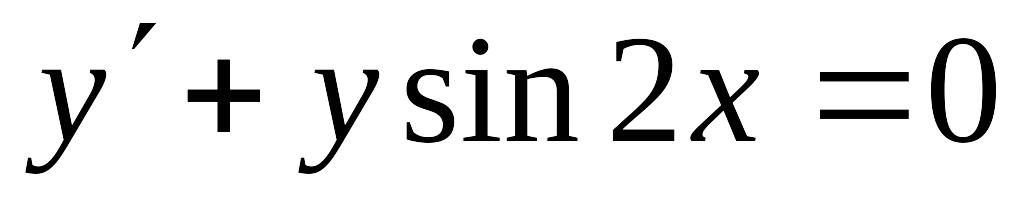 ,
,



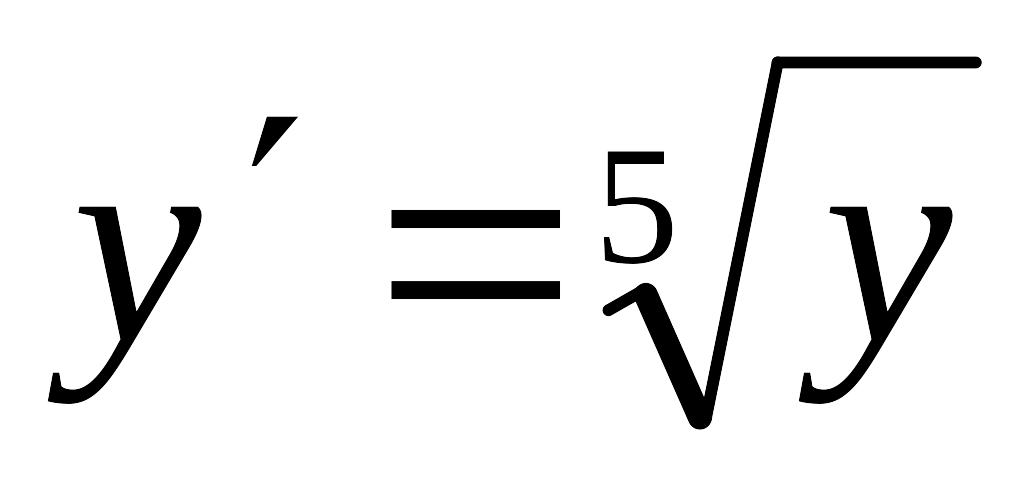 ,
, 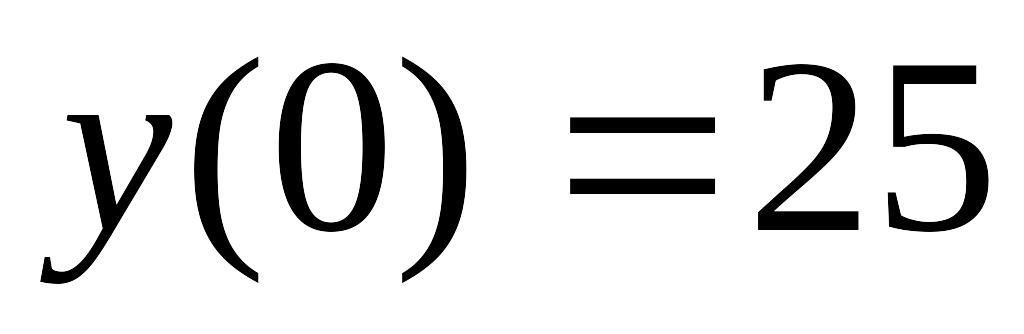


Розв’язати однорідні диференціальні рівняння
 ;
; ;
; ;
; ;
; ;
;
Контрольні запитання.
Яке рівняння називають диференціальним ?
Як визначають порядок диференціального рівняння ?
Яку функцію називають розв’язком диференціадьного рівняння ?
Скільки розв’язків може мати диференціальне рівняння ?
Який розв’язок диференціадьного рівняння називають загальним ?
Який розв’язок диференціадьного рівняння називають частковим ?
Як знайти частковий розв’язок диференціадьного рівняння ?
Яку задачу називають задачею Коші ?
Скільки початкових умов повинна мати задача Коші ?
Запишіть загальний вигляд диференціального рівняння з відокремлюваними змінними.
Якою є схема розв’язку диференціальних рівнянь з відокремлюваними змінними?
Яким є загальний вигляд однорідного диференціального рівняння І порядку?
Яку умову повинно задовільняти однорідне диференціальне рівняння І порядку?
Якою є схема розв’язку однорідного диференціального рівняння І порядку?
Тема: Розв’язування лінійних диференціальних рівнянь І порядку Розв’язування рівнянь
Бернуллі в повних диференціалах.
Мета: Навчитись розв’язувати лінійні диференціальні рівняння І порядку та рівняння
Бернуллі
Література:
