4.2.3 Радикальна ознака Коші

Якщо для додатного числового ряду існує

(4.7)

то при К<1 ряд збігається, а при К>1 ряд розбігається.

• Зауваження 3. Радикальна ознака Коші найчастіше використовуються у випадках, коли загальний член ряду містить n в основі та в показнику степеня.

• Приклад. Дослідити збіжність ряду

Розв’язання. Знайдемо сталу Коші:

За радикальною ознакою Коші заданий ряд збігається.

4.2.4 Інтегральна ознака Коші

Нехай треба дослідити збіжність ряду , де a_n = f(n). Розглянемо невластивий інтеграл , в якому підінтегральна функція одержана шляхом заміни аргумента n на аргумент х в функції f(n).

Якщо невластивий інтеграл збігається, то числовий ряд також збігається. Якщо невластивий інтеграл розбігається, то числовий ряд також розбіжний.

• Зауваження 4. Інтегральна ознака Коші є найбільш сильною ознакою. Цю ознаку використовують у випадках, коли не працюють ознака Даламбера (D=1) та радикальна ознака Коші (К=1).

• Приклад. Дослідити збіжність узагальненого гармонічного ряду .

Розв’язання. Застосуємо інтегральну ознаку Коші. Оскільки , то . Розглянемо невластивий інтеграл

Отже, невластивий інтеграл та заданий ряд збіжні при р>1 і розбіжні при р1.

4.3 Оцінка залишку додатного числового ряду

Залишок r_n збіжного додатного числового ряду і абсолютна похибка заміни S частковою сумою S_n з точністю  > 0 досягається при такому n, що . Для знаходження такого номера n використовують наступні твердження теореми про оцінку залишку ряду.

• Теорема. Якщо усі члени збіжного додатного ряду не перевищують відповідних членів другого збіжного додатного ряду , то залишок r_n ряду не перевищує залишок 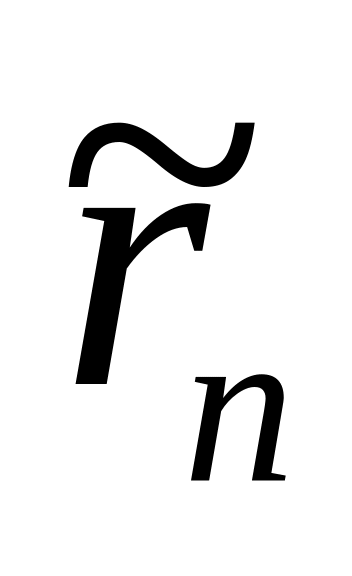ряду .

Найчастіше в якості допоміжного ряду обирають ряд, залишок якого можна обчислити (наприклад, ряд геометричної прогресії).

• Приклад. Оцінити r₃ ряду

Розв’язання. Кожен член заданого ряду менший відповідного члена ряду геометричної прогресії , тому

4.4 Знакозмінні числові ряди

• Означення 3. Ряд називається знакозмінним, якщо він містить нескінченну кількість як додатних, так і від’ємних членів. Ряд, члени якого по черзі мають додатний та від’ємний знаки, називають знакопочережним.

4.4.1 Поняття абсолютної та умовної збіжності ряду

• Означення 4. Знакозмінний ряд називають абсолютно збіжним, якщо збігається ряд із абсолютних величин членів знакозмінного ряду.

• Означення 5. Знакозмінний ряд називається умовно збіжним, якщо цей ряд збігається, а ряд із абсолютних величин його членів розбігається.

Для виявлення умовної збіжності знакопочережного ряду використовують наступну ознаку.

Ознака Лейбніца. Якщо абсолютні величини членів знакопочережного ряду монотонно спадають і границя абсолютної величини загального члена ряду дорівнює нулю при n → ∞, то ряд збігається, причому його сума S не перевищує першого члена ряду.

Цю ознаку коротко можна записати так

• Приклад. Дослідити збіжність рядів:

а) б)

Розв’язання.

Ряд а) – знакозмінний, оскільки

Розглянемо ряд , складений з абсолютних величин членів ряду. Цей ряд є узагальненим гармонічним рядом з показником степеня р = 2 > 1, тому він збіжний. Згідно означенню це означає, що ряд а) абсолютно збіжний.

Ряд б) – знакопочережний. Ряд , складений з абсолютних величин його членів розбігається, оскільки це гармонічний ряд. Це означає, що ряд б) абсолютно не збігається.

Оскільки обидві умови ощнаки Лейбніца для ряду б) виконуються:

1) , 2) ,

то цей ряд збігається умовно.