29

Державний університет телекомунікацій

Навчально-науковий виробничий центр, м. Львів

Затверджую

Зав. ННВЦ

__________ Яковлєва Т.С.

“___” _______ 2014 р.

Опорний конспект лекцій

з дисципліни “Вища математика”

для студентів заочної, прискореної форми навчання

(ІІІ курс, V семестр), лекція 3

Розділ 4. Ряди та гармонічний аналіз

Склав: доцент, к.ф.-м.н.

Плешівський Я.М.

м.Львів-2014 р.

План лекції

• Числові ряди:

• загальні поняття, необхідна ознака збіжності ряду;

• достатні ознаки збіжності додатних числових рядів;

• порівняльні ознаки;

• ознака Даламбера;

• радикальна ознака Коші;

• інтегральна ознака Коші;

• оцінка залишку додатного числового ряду;

• знакозмінні числові ряди.

• Функціональні та степеневі ряди:

• функціональні ряди;

• cтепеневі ряди;

• область збіжності та властивості степеневих рядів;

• розклад функцій в степеневий ряд та його застосування.

• Гармонічний аналіз:

• гармоніка та ортогональні системи функцій;

• ряди Фур’є;

• перетворення Фур’є;

• амплітудно-частотні характеристики сигналів.

4 Числові ряди

4.1 Загальні поняття. Необхідна ознака збіжності ряду

Числовим рядом називають суму нескінченної кількості числових доданків і записують, використовуючи символ суми, так:

(4.1)

Числа а₁, а₂, ..., а_n, … називають членами ряду: а₁ – перший член ряду, а₂ – другий член ряду, ... а_n – n-й або загальний член ряду.

Ряд вважається заданим, якщо відомий загальний член а_n як функція номера:

Наприклад, загальним членом ряду

буде

Іноді задають декілька перших членів ряду і треба записати увесь ряд, тобто знайти його загальний член. При цьому загальний член ряду треба знаходити у вигляді функції простішого виду. Наприклад, при знаходженні загального члена ряду

маємо:

, , , .

Кожен член ряду є дробом, чисельник якого дорівнює одиниці, а знаменник є добутком двох множників n та 2ⁿ. Тому загальним членом ряду буде і ряд пиймає вигляд .

• Означення 1. Частковою сумою числового ряду (4.1) називають суму S_n перших n членів ряду:

S_n = а₁ + а₂ +…+ а_n.

• Означення 2. Числовий ряд називають збіжним, якщо існує скінченна границя послідовності його часткових сум S_n при n, тобто

(4.2)

Якщо S є сумою збіжного ряду (4.1), то пишуть

Якщо границя часткових сум (4.2) не існує або дорівнює , то ряд називають розбіжним.

• Приклад. Дослідити збіжність ряду .

Розв’язання. Оскільки

то маємо:

Тому

Отже, часткова сума заданого ряду має границю, яка дорівнює 1. Це означає, що цей ряд збіжний і його сумою буде 1.

• Приклад. Дослідити збіжність ряду

1 – 1 + 1 – 1 +...+ (-1)^n-1 +...

Розв’язання. Часткові суми заданого ряду мають вигляд

S₁ = 1; S₂ = 0; S₃ = 1; S₄ = 0; ...

Оскільки границя послідовності залежить від способу прямування n до нескінченності, то за означенням границі не існує і заданий ряд – розбіжний.

Часто використовують наступні числові ряди:

1. Гармонічний ряд 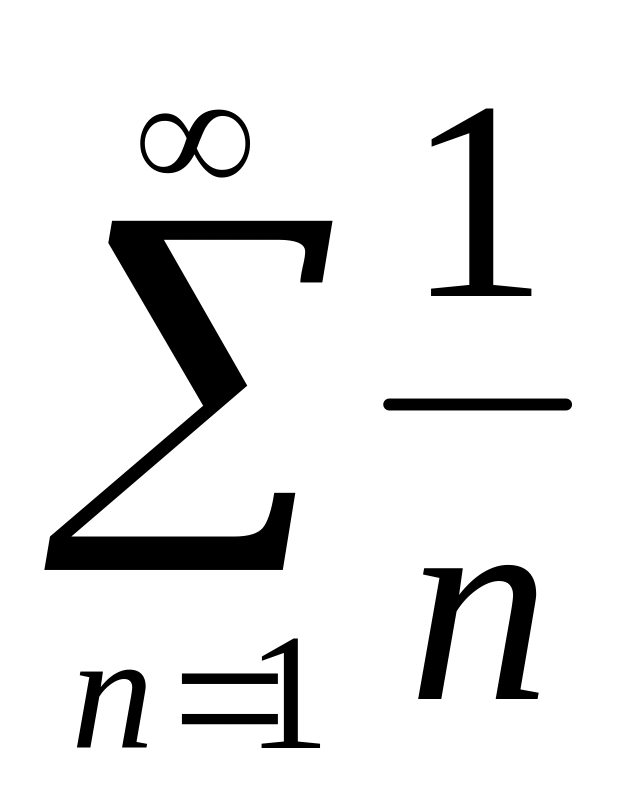. Цей ряд розбіжний.

2. Ряд геомеричної прогресії з першим членом а та знаменником q. Цей ряд збігається при ; має суму , а при 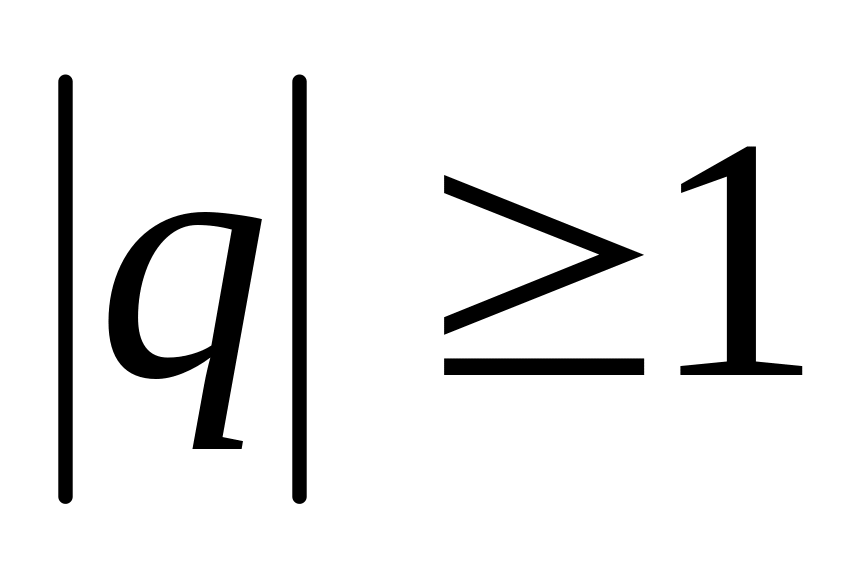ряд – розбіжний

3. Узагальнений гармонічний ряд . Цей ряд збіжний при р>1, а при р1 – розбіжний.