7. Декодирование математической модели.

Декодирование – это переход от кодированных факторов к натуральным с помощью подстановки.

,

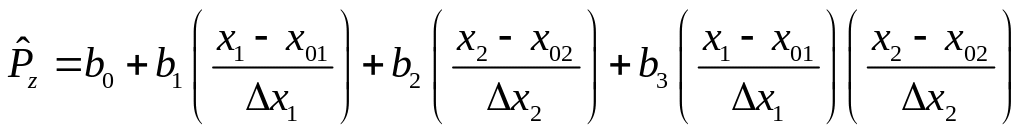в нашем случае:

После раскрытия скобок и приведения подобных членов получаем полином вида:

. (13)

Приведем алгоритм для расчета коэффициентов M_j модели (13).

(14)

8. Анализ математической модели.

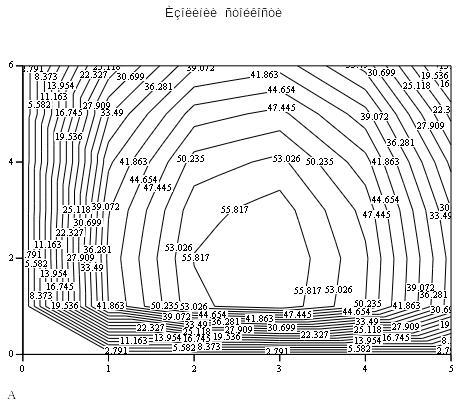
Построим топографию (рис. 4) модели (13).

0.3

331

500

270

140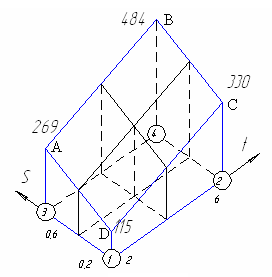

Рис. 4

Топография полинома ABCD представляет собой плоскость общего положения АВ # СD и BC # AD, т.к. b₃ .

9. Выводы

1. Для получения двухфакторной модели методом планируемого эксперимента достаточно поставить 17 опытов

2. В исследованной области на усилие резания сильнее влияет глубина резания.

3. Зависимость усилия резания от режимов аппроксимируется полином первой степени с взаимодействием факторов

.

Контрольные вопросы

1. Что такое полный факторный эксперимент (ПФЭ)?

2. Как рассчитывается количество опытов в ПФЭ?

3. Назовите этапы ПФЭ.

4. Как выбирается тип модели?

5. Что такое матрица планирования?

6. Для чего выполняется кодирование факторов?

7. Назовите этапы кодирования факторов.

8. Что представляет собой область варьирования факторов двухфакторного эксперимента?

9. Что представляет собой область варьирования кодированных факторов двухфакторного эксперимента?

10. Раскройте алгоритм формирования матрицы планирования для k факторов.

11. Какими свойствами обладает матрица планирования?

12. В какой последовательности реализуются опыты матрицы планирования?

13. Назовите этапы статистической обработки ПФЭ.

14. Как проверяется однородность выборочных дисперсий?

15. Как рассчитываются коэффициенты математической модели?

16. Как проверяется значимость коэффициентов модели?

17. Как проверяется адекватность модели?

18. Как выполняется декодирование математической модели?

19. Что включает в себя анализ математической модели?

ЛАБОРАТОРНОЕ ЗАНЯТИЕ № 2

Экспериментальная оптимизация геометрии инструмента

1. Анализ проблемы.

Рассматривается операция фрезерования плоскости в заготовке из жаропрочной стали Х12Н20Т3Р цилиндрической фрезой со вставными ножами из быстрорежущей стали Р12Ф4К5 при следующих условиях (рис. 1):

1) диаметр фрезы D_ф = 90 мм.;

2) глубина резания t = 2 мм.;

3) ширина фрезерования В = 16 мм.;

4) подача на зуб S_z = 0,047 мм/зуб.;

5 скорость резания V = 22 м/мин.

Рис. 1.

Для сокращения расхода инструмента в условиях рыночного производства необходимо экспериментально найти оптимальные значения заднего и переднего углов, обеспечивающих для заданных условий (рис.1) максимальную стойкость фрезы, т.е.

Т ( , ) = max

2. Постановка задачи исследования.

Для заданных условий фрезерной операции (рис. 1) найти экспериментально симплексным методом значения переднего  и заднего  углов зуба фрезы, обеспечивающих максимальное значение её стойкости Т.

3. Поиск оптимальной геометрии симплексным методом.

Симплексный поиск включает следующие этапы.

3.1. Выбор базовых значений и интервалов варьирования факторов

Из справочника [1] выбираем следующие рекомендуемые значения (табл. 1)

Таблица 1.

Xj		X0j	∆X
X1		270	40
X2		170	40

3. 2. Расчет координаты вершин начального симплекса.

Кодированные координаты первой вершины начального симплекса рассчитываются по формуле

где J – номер фактора.

Значения кодированных координат других вершин формируются по алгоритму табл. 2

Таблица 2.

№ вер- шины	Х1		Х2
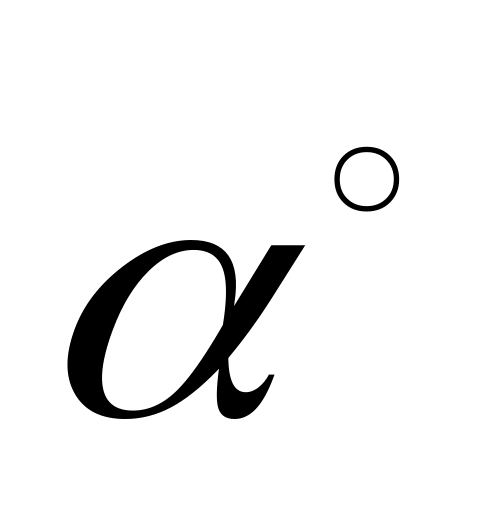
	Z1		Z2
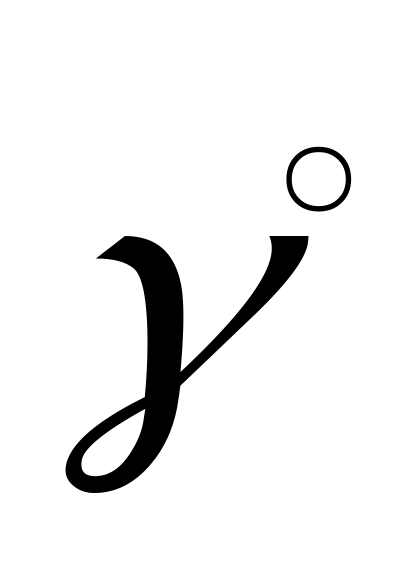
1	0,5	29	0,289	18
2	-0,5	25	0,289	18
3	0	27	-0,578	15

Рассчитаем натуральные координаты вершин начального симплекса:

; x_j=x_oj+∆x_j∙z_j

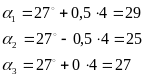
3.3. Реализация опытов для координат вершин

начального симплекса.

В каждой вершине симплекса опыты повторялись три раза для повышения устойчивости поиска, и средние значения стойкости записывались нижнюю строку табл. 3.

3.4. Поиск худшей вершины.

При поиске максимальной стойкости худшей вершиной в первом (начальном) симплексе будет первая вершина с минимальной стойкостью Т = 18.2 мин.

3.5. Расчёт координат отражённой вершины

Для двух факторов симплекс представляет собой правильный треугольник, для которого координата отражённой вершины рассчитывается как сумма координат лучших вершин за вычетом координаты худшей вершины. В нашем случае координаты отражённой вершины 4

₄ = ₂ + ₃ - ₁ = 25 + 27 – 29 = 23

₄ = ₂ + ₃ - ₁ = 18 + 15 – 18 = 15

3.6. Реализация опытов в отражённой вершине

Опыты в 4 – й вершине дали значение стойкости Т = 44.7 мин.

Затем этапы 3.4, 3.5 и 3.6 циклически повторяются до кругового зацикливания симплекса вокруг экстремальной точки.

Динамика геометрии и стойкости инструмента в процессе симплексного поиска приведена в табл. 3 и графически отражена на рис. 2.

Таблица 3.

№ верши- ны	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15(8)
	29	25	27	23	25	21	23	19	21	17	19	15	12	15	19
0	18	18	15	15	12	12	9	9	6	6	3	3	6	9	9
Т, мин.	18.2	32,5	34	44,7	45,7	53	53,7	57,6	57,9	58,3	58,2	55,1	51,9	54,7	57,6

18

15

12

9

6

3

18.2

32.5

							44.7 44.718.2		II
	I					53		IV	III	34
			54.7			57.6	VI	V		45.7
		51.9		XII	XIII	VIII	VII		53.718.2
				XI	58.3 X	IX		57.9
			55.1				58.2				

5 7 9 11 13 15 17 19 21 23 25 27 29

Рис. 2

В процессе поиска имело место линейное зацикливание симплексов IX и X относительно ребра 10 - 11. Для выхода из зацикливания в десятом симплексе отражаем следующую худшую вершину 11.

Симплексный поиск прекращен в виду кругового зацикливания вокруг экстремальной точки 10 с координатами ₀=17^о и ₀=6^о, в которой достигается максимальная стойкость зуба фрезы Т_max = 58.3 мин.

4. Выводы

1. Зависимость стойкости инструмента от его геометрии носит экстремальный характер.

2. Максимальная стойкость Т_max = 58.3 мин. достигается при ₀=17^о и =6^о в десятой вершине VIII симплекса.

3. Для поиска максимума было поставлено 14 опытов.

4. Оптимизация позволила повысить стойкость, по сравнению с нормативной, в К_Т раз

СПИСОК ЛИТЕРАТУРЫ

1. Прогрессивные режущие инструменты и режимы резания металлов. Под. ред. В. И. Баранчикова. – М.: Машиностроение, 1990. – 400 с.

Контрольные вопросы

1. Как формулируется задача поиска оптимальной геометрии?

2. Оптимальные значения каких улов находятся в результате поиска?

3. По какому критерию оценивается оптимальная геометрия?

4. Для какой операции выполняется поиск оптимальной геометрии?

5. Как определяется количество вершин симплекса?

6. Как рассчитываются координаты отраженной вершины?

7. По какой причине прекращен симплексный поиск?

8. Как рассчитываются кодированные координаты начального симплекса?

9. Какие виды зацикливания симплекса Вам известны?

10. Как выходить из зацикливания?

ПРОГРАММА MATHCAD

для моделирования стойкости инструмента

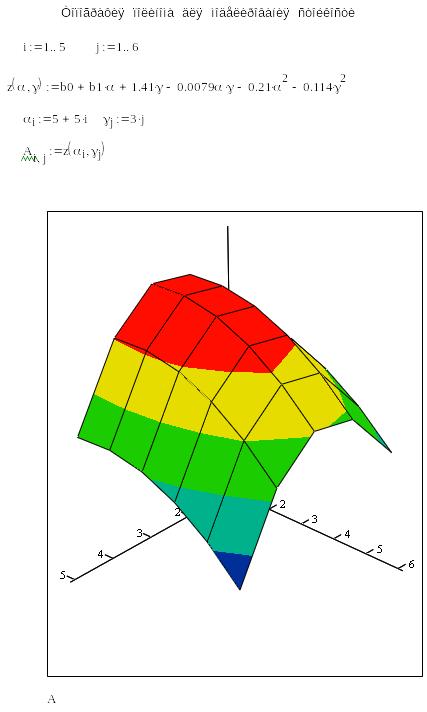
ЛАБОРАТОРНОЕ ЗАНЯТИЕ №3.

формирование аналитической модели технологическаой операции

1. Анализ технологической операции.

В порядке сравнения анализируем рассмотренную выше операцию продольного точения (рис. 1).

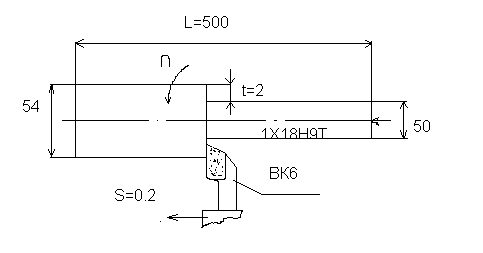
Рис. 1

2. Постановка задачи

Для заданных условий токарной операции (рис. 1) найти частоту n, обеспечивающую максимальную прибыль Р и гарантирующую требуемое качество обработки.

3. Разработка математической модели.

3.1 Целевая функция.

Принципиальная зависимость для прибыли предложена японски-

ми учёными Окусима и Хитоми.

Р= , (1)

где: С - цена реализации детали, руб.;

С_M - стоимость материала для одной заготовки, руб.;

Т_о - время на изготовление партии деталей, мин.;

t - трудоемкость изготовления одной детали, мин.;

С - себестоимость изготовления одной детали, руб.

Подставив в выражение (1) раскрытые ранее зависимости для t и С, получим выражение для критерия Р в развернутом виде.

Р= (2)

3.2 Технические ограничения.

Т_max ³ Т ³ t₀ (3)

n Î n_ст (4)

4. Анализ математической модели.

Целевая функция (2) нелинейная, одномерная зависимость прибыли от частоты n, имеющая максимум при n₀. Выполним численный и графический анализ прибыли и её элементов в диапазоне частот, допус-каемых ограничениями (3) и (4) при следующих дополнительных данных:

Сд=9 руб.; См=4 руб.; То=2´8´60=960 мин.

Для этих условий целевая функция принимает следующий вид:

Р= > 0 (2а)

Расположим расчётные зависимости в алгоритмическом

порядке (табл. 1).

Таблица 1

Мат. мод.	№ пп	Наименова- ние	Обо- знач.	Формула	Расчётная зависимость
Це- ле- вая функ- ция	1	Основное время	t0	L/(Sn)	500/(0.2n)
	2	Стойкость	Т	Ст/nм	7х1012/n4
	3	Инструм. время	tи	t1t0/Т	6t0/Т
	4	Трудоём- кость	t	tв + t0 + tи	4 + t0 + tи
	5	Стоимость всп. врем.	Сtв	С1tв	0.17х4=0.68
	6	Пост. затр. на инстр.	Ки	С1t1+ Сз+(Сн-Сиз)/ (z1+1)	0/17х6+1.7+(40-5)/ (5+1)= 8.55
	7	Стоимость осн. врем.	Сt0	С1t0	0.17 х t0
	8	Стоим. ин- стр. затрат	Си	Киt0/Т	8.55 х t0/Т
	9	Себестои- мость	С	Сtв+ Сt0+ Си	0.68+ Сt0+ Си
	10	Прибыль	Р	Р=(С - Cм - С)Т0/t	(9- 4 - С)960/t
Техн. огран.	11	По стойко- сти	Т	400 ³ Т ³ t0
	12	По частоте	n	n Î ncт

Протабулируем значения прибыли и её элементов по табл. 1.

Результаты табулирования приведены в табл. 2.

Таблица 2

n	100	200	300	400	575	600	700	800	900	1000
t	29	17	13	10	-	8.6	8.3	8.3	8.34	8.54
C	4.93	2.83	2.18	1.94	-	2.05	2.33	2.77	3.38	4.16
P	2.19	125	217	283	332	331	313	267	197	106

Выполним графический анализ для протабулированных значений

(рис. 2).

									С	Р
10							Р		5	300
9,5									4	250
9	С								3	200
8,5									2	150
								n

100 200 300 400 500 600 700 800 900 1000

Рис. 2

Согласно рис. 2 зависимость прибыли от частоты носит экстремальный характер. При низких частотах прибыль мала из-за высокой трудоемкости  и себестоимости С. При высоких частотах прибыль уменьшается из-за снижения стойкости инструмента Т и повышения затрат на режущий инструмент С_и.

Критерий трудоемкость применяется в экстремальных условиях, когда за короткое время необходимо произвести максимальное количество деталей.

Себестоимость - при плановом изготовлении изделий.

Прибыль - при изготовлении и реализации запасных и ремонтных деталей.

5. Методы оптимизации.

В данном случае, ввиду сложного выражения целевой функции, для поиска экстремума могут применяться численные методы: половинное деление, золотое сечение, сканирование и др.

Рассмотрим алгоритм сканирования с интервальным уточнением (рис. 2, рис. 3, табл. 3).

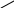
1. n₁, n₂, Dn

2. P_max=0, u=1

3. n=n₁

4. P=f(n)

_

5. P>P_max

+

6. P_max=Р

n_o=n

7. n=n+Dn

+

8. n£n₂

9. u, n_o, P_max

10. u=u+1

11. u£3

+ Таблица 3

12. u	n1	n2	Δn	n0
    1	200	1000	100	600
    2	500	700	20	560
    3	510	580	4	576

    n₁=n_o-Dn

n₂= n_o+Dn

Dn=Dn/5

13. u , n_o, P_max

Рис. 3

7. Выводы

1. Зависимость прибыли от частоты носит экстремальный характер

(max).

2. Максимальная прибыль Р=332 руб. достигается при

n₀=575 1/мин.

3. Оптимизация позволила увеличить прибыль в

К_р = Р₅₇₅ / Р₄₀₀ = 332 / 283 = 1.17 раза.

4. Зависимость прибыли от частоты имеет остро выраженный характер, так как критерий Р учитывает больше технико-экономической информации.

Контрольные вопросы

1.По какому критерию выполняется оптимизация режимов резания?

2. Как формулируется задача оптимизации режимов резания?

3. Какие критерии включает критерий оптимизации?

4. Сколько неизвестных в рассматриваемой задаче?

5. Какие технические ограничения учитываются при решении задачи?

6. Что представляет собой целевая функция?

7. Почему критерий экстремально зависит от режимов резания?

8. Как формулируется ограничение по стойкости режущего инструмента?

9. Как позиционируются оптимальные режимы для основных критериев?

10. Какими методами решается задача оптимизации?

ЛАБОРАТОРНОЕ ЗАНЯТИЕ №4.