8Всякая ли неограниченная послед-ь является бесконечно большой? Ответ обоснуйте.
Любая бб послед-ь является неограниченной. Однако неограниченная послед-ь может и не быть бб послед-ью. Например, неограниченная послед-ь 1, 2, 1, 3 .., 1, n, 1, n + 1 … не является бб, поскольку при А > 1 неравенство |Xn| > A не имеет места для всех элементов Xn с нечетными номерами.
9.lim(xn+yn)=limxn(=a)+limyn(-b). Z=xn+yn limz=a+b . Док-во начиная с n0 a-e/2<xn<a+e/2 и тоже с y=>cумма=> |zn-(a+b)|<e
10 Докажите, что предел произведения двух функций равен произведению их пределов, если последние существуют.
Pn=xn-a tn=yn-b – б.м. limxnyn=lim(a+pn)(b+bn)=…=ab
11.f(x)=o(g(x)) x->x0 – f(x) – б.м. более высокого порядка.При каком целом n |x|^8/5=o(x^n) x->0 lim a/b=0 n>8/5
12. Докажите, что сходящаяся послед-ь имеет только один предел От противного Предп, что некоторая послед-ь {Xn} имеет 2 разл предела а и b, a ≠ b.
Выберем столь малые окрестности т. a и b, чтобы они не имели общ точек. Т.к. lim Xn = a, все Xn, начиная с нек номера n1, содержатся в выбран окрестности т. а; точно так же из lim Xn = b, следует, что все Xn, начиная с нек номера n2, содержатся в выбранной окрестности т. b. Положим, n0 = max {n1, n2}. Тогда числа Xn с номерами n≥ n0 должны принадлежать как первой, так и второй окрестности, что невозможно, так как окрестности не имеют общих точек.
13. Докажите ограниченность сход послед-и /док-во:
Зафиксируем е>0. Т.к. хn сходится, то с нек. N0 выполняется a-e<xn<a+e Это значит, что множ. Таких хn, что n>n0 огр. С др. стороны множество n, таких, что n<=n0 конечно, т.е ограничено =>объединение этих множ-в ={xn,n€N} тоже огр.
14Докажите, что произведение бм и ограниченной послед-ей является бм послед-ью.
док-во:
Пусть {Хn} – ограниченная, а {αn} – бм послед-и. Доказать, что {Xn * αn} – бм. Так как {Хn} ограниченна, то существует число А > 0 такое, что любой элемент Хn удовлетворяет неравенству | Хn | ≤ А. Возьмем любое ε > 0. Поскольку {αn} – бм, то для положительного числа ε/А существует номер N такой, что при n > N выполняется неравенство | αn | < ε/А. Тогда при n > N |Xn * αn | = |Xn| * | αn | < A * ε/A = ε. Это означает, что послед-ь {Xn * αn} – бм.
15. Может ли послед-ь {Xn + Yn} сходиться, если послед-ь {Xn} сходится, а послед-ь {Yn} расходится? Ответ обоснуйте.
нет, не может:x+y=z z-x-сход.z-x=y –не может
16. Докажите, что функция f(x) = sin 1/x не имеет предела в точке x = 0.
lim (x→0) sin 1/x по Гейне lim (n→∞) Xn = X0, lim(x→0+0) 1/x = +∞, lim(x→0-0) 1/x = - ∞
lim (x→0+0) sin 1/x – не сущ. sin (x→0-0) 1/x – не сущ.
17. Может ли функция f(x) +g(x) быть непрерывной в точке х0, если функция f(x) непрерывна, а функция g(x) имеет разрыв в этой точке, а функция g(x)имеет разрыв в этой точке. ответ обоснуйте.
Нет.
Так как есть теорема, в которой говорится.
Если f(x) и g(x)- непрерывные функции в точке
x0, то непрерывными являются
.
.f(x)=c-является непрерывной и f(x)=x.
18 Найдите значение а, при котором функция f(x) =1) (x^2-3x)*cos(1/x),x=/0;2) a, x=0 непрерывна в 0. Lim(1)=0, то а=0
19определение
производной в точке
Пусть функция
определена в некоторой окрестности
точки x0(∆x=x-x0).
Производной
функции
в точке x0
называется lim
,
когда
(при условии, что lim
существует). Обозначение
.(x->x0)
Lim=((x0+^x)^1/2-x0^1/2)/^x=
lim(x^1/2-x0^1/2)/(x-x0)=
lim1/(x^1/2+x0^1/2)=1/2
*x0^(-1/2)
20. f(x)=sinx, xо-произвольное число
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f
′(xо)=
=
=
=cosx0
21
f(x)=
,
xо
=1
=
=
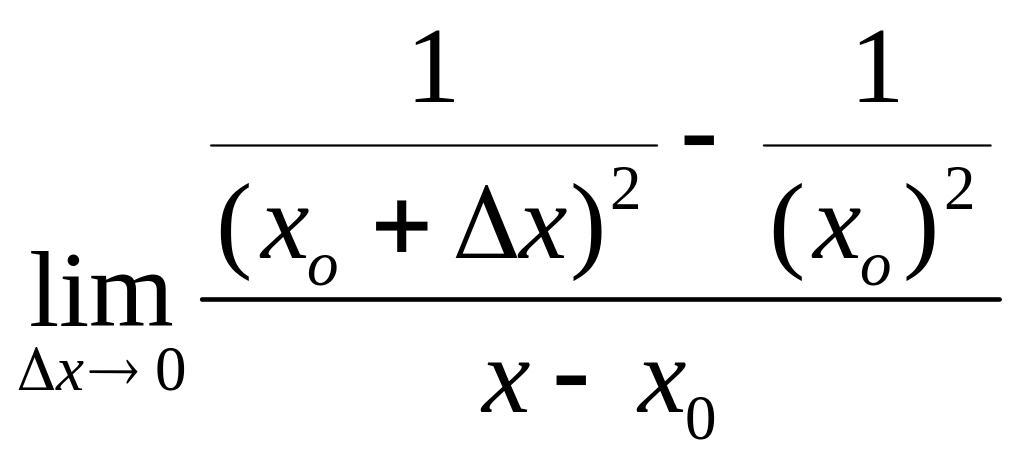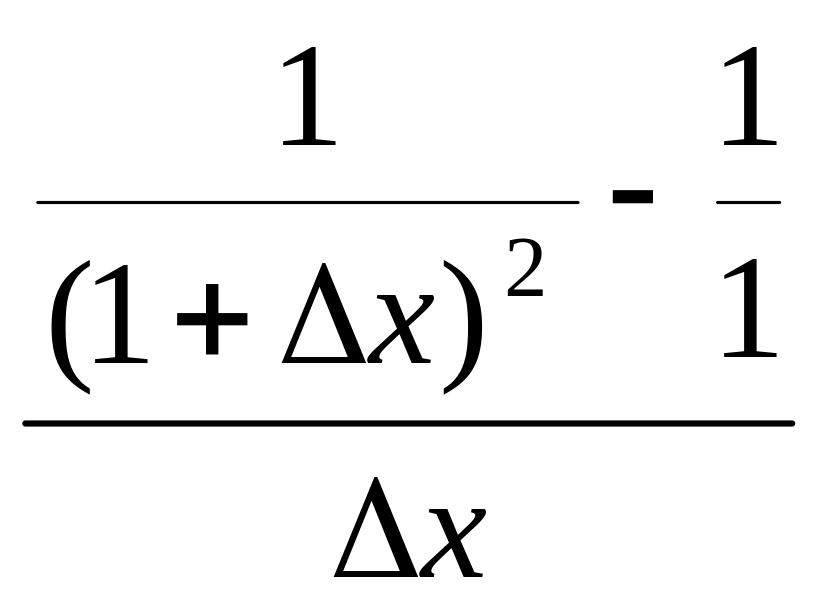=-2
22 f(x)=xx, x0=0
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
23
27f(x) = 3x , x0 = 5.
Эластичностью
функции y
= f(x)
в точке х0
называется предел
E(x)=
