Определение динамических параметров объекта

При расчетах АСР объекты легкой промышленности во многих случаях аппроксимируются апериодическим звеном первого порядка с запаздыванием. То есть динамическая модель объекта описывается передаточной функцией вида: . (13)

Передаточная функция – отношение изображения выходного сигнала к входному при нулевых начальных условиях. Изображение функции – функция независимого комплексного переменного р, полученная путем преобразования Лапласа функции времени t.

Динамические параметры объекта – коэффициенты, входящие в формулу передаточной функции ТОУ: k – коэффициент передачи, T – постоянная времени, τ – время запаздывания.

Постоянная времени, Т – время за которое кончился бы переходной процесс, если бы скорость изменения выходной величины осталась постоянной с начала изменения входного сигнала. Определяет инерционность звена. Чем больше Т, то есть больше инерционность, тем продолжительнее переходный процесс.

Время запаздывания, τ – время между подачей входного сигнала и появлением реакции на него (изменения выходного сигнала).

Дифференциальное уравнение объекта, описываемое передаточной функцией (13), имеет вид: , (14)

здесь y(t) – выходной сигнал объекта, x(t) – входной сигнал объекта

Решением уравнения (14) при нулевых начальных условиях будет уравнение переходной характеристики: 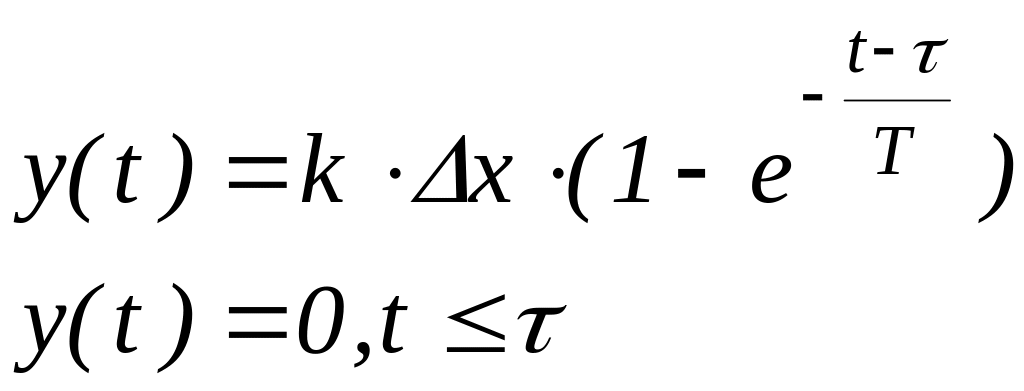, (15)

где Δx – входной сигнал объекта.

Учитывая начальные условия и формулу (12), уравнение переходного процесса имеет вид: 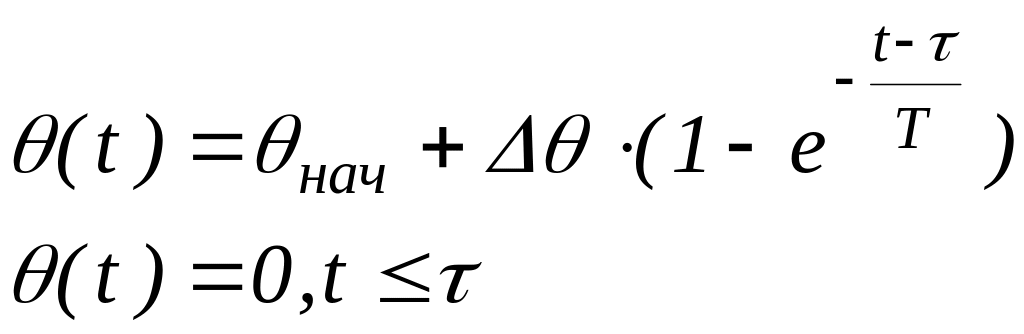, (16)

где Δθ = θ_уст- θ_нач – приращение выходного сигнала (температуры), θ_уст – установившееся значение температуры, θ_нач – начальное значение температуры.

Для определения постоянной времени Т и времени запаздывания τ по экспериментальной кривой переходного процесса применяют графоаналитические методы.

Метод Орманса

Расчет основан на обработке координат двух характерных точек по оси ординат: 0.33Δθ и 0.7Δθ (рис.11). Из этих точек проводятся линии параллельные оси абсцисс до пересечения с переходной характеристикой. Затем из полученных точек опускаются перпендикуляры на ось абсцисс и, определяются соответственно значения времени t_0.33 и t_0.7.

Далее, используя эти значения, по формулам Орманса рассчитываются динамические параметры: постоянная времени и время запаздывания: . (17)

С ледует заметить, что время запаздывания, рассчитываемое по формуле Орманса – это «переходное» запаздывание τ_п. Различают также «чистое» запаздывание τ_ч – время, которое проходит с момента подачи входного сигнала до того момента, как начнет изменяться выходной сигнал (отрезок ОВ). В этом случае полное запаздывание: .

Метод характерных точек

Э тот метод пригоден для кривых разгона, не имеющих выраженной точки перегиба (рис.12). В этом случае переходное запаздывание отсутствует: . Расчет динамических параметров, по аналогии с методом Орманса, основан на обработке координат двух характерных точек по оси ординат: 0.63Δθ и 0.87Δθ. Из этих точек проводятся линии параллельные оси абсцисс до пересечения с переходной характеристикой. Затем из полученных точек опускаются перпендикуляры на ось абсцисс и определяются соответственно значения времени t_0.63 и t_0.87. Далее рассчитывается постоянная времени: . (18)