Дорогие восьмиклассники!

Поздравляем вас с началом учебного года! Мы надеемся, что все вы за лето достаточно отдохнули и готовы приступить к занятиям.

В этом году мы продолжим изучение алгебры и геометрии, которое мы начали в 7 классе. Вы значительно расширите свои математические познания и умения. До сих пор вам были известны из алгебры только рациональные числа, целые выражения и линейные уравнения, в 8 классе вы ознакомитесь с действительными числами, рациональными выражениями и квадратными уравнениями. Следовательно, научитесь решать и такие задачи, которые прежде решать не умели. Геометрия же откроет вам новые фигуры – четырехугольники, расскажет об их свойствах, познакомит с одной из самых замечательных теорем – теоремой Пифагора, откроет вам новые свойства уже знакомых вам по 7 классу треугольников. При изучении геометрии в 8 классе вы будете, не только учиться логично и последовательно мыслить, но и развивать свои способности самостоятельно совершать открытия.

В каждом предложенном уроке есть и теоретический материал, и образцы решения заданий, и домашние задания. Домашние задания выполняйте в отдельной тетради, которую потом сдадите учителю. В конце темы предлагается контрольная работа. Ее тоже можно выполнить в этой тетради.

Рекомендованные учебники:

Алгебра: учебник для 8 кл. общеоразоват. учеб. заведений / Г.П. Бевз, В.Г. Бевз. – К.: Зодиак-Эко, 2008.

Геометрия: 8: двухуровн. учеб. для общеоразоват. учеб. заведений / Г.В. Апостолова. – К.: Генеза, 2008.

Учебники можно получить у классного руководителя или найти на сайте: shkola.yccat.com

Желаем удачи!

Геометрия.

Тема 1: «Повторение. Четырехугольники. Параллелограммы». Урок 1: Повторение. Начальные геометрические сведения.

На этом уроке вспомним аксиому о параллельных прямых и следствие из нее. Повторим определение луча и угла и единицы измерения отрезков и углов. Вспомним определение равных геометрических фигур и то, как сравнивают и измеряют отрезки и углы. Вспомним, что такое середина отрезка и биссектриса угла, какие углы называются острыми, прямыми и тупыми. Повторим теоремы о сумме смежных углов и о равенстве вертикальных углов. Вспомним, что такое перпендикулярные прямые и теорему о том, что две перпендикулярные к третьей прямые не пересекаются. И будем решать типовые задачи на повторенный материал.

1. Повторение начальных геометрических сведений

Вспомним сведения, изученные в текущей теме:

- Аксиома. Через две точки можно провести прямую, и только одну.

- Прямые на плоскости могут пересекаться, могут не иметь общих точек.

- Угол измеряется в градусах. 1 градус – это сто восьмидесятая часть от развернутого угла.

- Сумма смежных углов равна 180^о.

- Вертикальные углы равны между собой.

- Прямые, пересекающиеся под углом 90^о, называются перпендикулярными.

- Прямые, перпендикулярные одной прямой, не пересекаются.

2. Пример 1

Пример 1: Найти угол между биссектрисами смежных углов.

Решение:

                                          

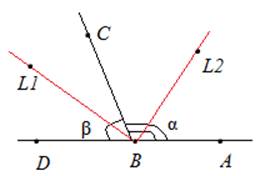
Рис. 1. Чертеж к примеру 1

Биссектриса BL₁ угла DBC = β делит его на два угла, градусная мера которых равна  . Биссектриса BL₂ угла АBC = α делит его на два угла, градусная мера которых равна  . Необходимо найти угол L₁ ВL₂. Выполним сложение углов: L₁ ВL₂ = L₁ ВС + СВL₂ =  . Сумма углов α + β равна 180^о, поскольку данные углы – смежные.

Ответ: 90^о.

Отметим, что в данной задаче нам не было известно, какие градусные меры углов DBC и АBC, однако мы знаем, что их сумма равна 180^о.